• Introduzione
• 1.1 Campo di radiazione generico
• 1.2 Regione vicina, di Fresnel e di Fraunhofer
• 1.3 Fronte d'onda nelle varie regioni
• 1.4 Andamento della potenza
• 1.5 Configurazioni tipiche

Gli elementi di base della teoria delle antenne possono essere ridotti sostanzialmente a tre sole classi: l'elemento radiante o antenna trasmittente, il mezzo di propagazione dell'energia irradiata, l'elemento investito da tale energia. Quest'ultimo può essere un'antenna ricevente nel caso della suddetta teoria o un essere vivente (fig. 1.1) nel caso che più ci interessa per gli scopi del corso.

Pur essendo presenti nominalmente le stesse tre classi, é proprio l'orientamento dello studio l'elemento discriminante tra i due casi. Così se nella teoria delle antenne ha molta importanza la direttività del radiatore (che sostanzialmente può essere descritta come la capacità di irradiare energia in una o più direzioni privilegiate), essa perde completamente di interesse nello studio della interazione con tessuti biologici. In questo caso infatti è importante conoscere solo la direzione di provenienza e le caratteristiche di propagazione dell'onda incidente indipendentemente dal fatto che l'antenna irradi contemporaneamente in altre direzioni. Al contrario ci preme conoscere le caratteristiche del campo e.m. in prossimità del radiatore, cosa invece di scarso interesse nelle trasmissioni in cui si presuppone che il ricevitore si trovi a grande distanza dal trasmettitore.

Con queste premesse risulterà giustificata l'estrema semplicità della trattazione che non pregiudicherà tuttavia la focalizzazione dei punti di maggiore utilità per il prosieguo del corso.

 
Campo di radiazione generico

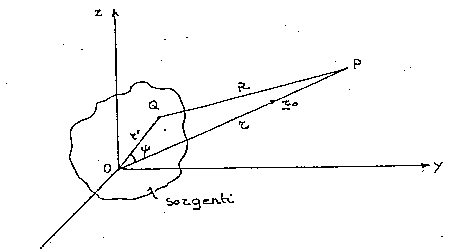
Ora, indipendentemente dal tipo di sorgente che irradia un determinato corpo biologico, il campo e.m. ad una certa distanza r da un'origine generica (fig. 1.2), può calcolarsi risolvendo l'equazione di Helmholtz, più nota nel dominio del tempo come "equazione delle onde" (direttamente ricavabile dalle equazioni di Maxwell):

Per semplicità ci siamo limitati a considerare solo il campo elettrico; per il campo magnetico vale un'equazione simile. Nell'eq. 1.1, k=nk₀ ove n è l'indice di rifrazione (n»1 nell'aria) e k₀ è il numero d'onda (k₀=w /c=w Ö (m ₀e ₀) sempre nell'aria). Inoltre f(r) indica la generica sorgente (eventualmente costituita da diverse sorgenti).

La semplice forma con la quale è espressa l'eq. 1.1 non deve trarre in inganno. La genericità del termine noto infatti rende il calcolo piuttosto complesso.

Sfruttiamo allora un'analogia tratta dalla teoria dei circuiti. In essa un particolare circuito o canale trasmissivo veniva descritto mediante una "risposta impulsiva" o ciò che è lo stesso, mediante la sua trasformata di Laplace nota come "funzione di trasferimento" (fig. 1.3). Dalla risposta all'impulso, che in un certo senso è una descrizione del comportamento della rete, è possibile ricavare facilmente la risposta ad una qualunque eccitazione. In formule, indicando con U e V le trasformate delle grandezze in uscita ed in ingresso rispettivamente, si ha:
 

con H(s)=funzione di trasferimento.
Analogamente nel dominio del tempo:

Fig.1.3 - Elementi caratterizzanti un generico canale.

Riguardo alla propagazione di un'onda e.m., sarà allora possibile una descrizione simile partendo dalla considerazione che l'atmosfera non è altro che un canale trasmissivo e come tale può essere descritto mediante una risposta impulsiva meglio nota in questo caso come "funzione di Green". Tale funzione rappresenta in realtà un campo e.m. L'eq. 1.1 diventa allora:

con d =funzione di Dirac. Essa può essere interpretata fisicamente come il gradiente della densità di carica r, come J o come rotore di J_m a seconda del campo che stiamo considerando ma tale da essere sempre zero tranne che per un punto, cioè quando r=r'. La soluzione per questa particolare sorgente risulta essere allora:

Anche in questo caso la semplicità di scrittura dell'eq. 1.5 non deve far pensare che la G sia una funzione facile da trattare, poiché R è legata ad una radice quadrata. Tuttavia sono possibili approssimazioni per ottenere risultati validi per il campo in certe zone dello spazio. E' in base all'entità di tali approssimazioni che si sviluppano i concetti di campo vicino e campo lontano.

Comunque nel caso generale il campo E, nota la funzione di Green, sarà ricavato da:
 

ove V è il volume contenente la (o le) sorgente generica rappresentata da f(r).

E' opportuno far notare che essendo nello spazio libero, l'unica condizione al contorno per G è quella di radiazione (cioè non entrano all'infinito flussi di potenza e non ci sono sorgenti all'infinito). Ciò spiega tra l'altro la presenza nell'eq. 1.5 del solo esponenziale negativo. Se ciò vale per G, varrà anche per E.

L'eq. 1.7 è un integrale di convoluzione spaziale e quindi può essere scritta anche nella forma:
 

 

che rende più evidente l'analogia con le funzioni di rete.

 
Regione vicina di, di Fresnel e di Fraunhofer
 
Riprendiamo l'espressione della funzione di Green definita nella eq. 1.5 approfondendone lo studio. Poiché le distanze sono, rispetto alla sorgente, molto grandi, intermedie e piccole, nasce un criterio di discriminazione tra le diverse regioni in cui è possibile applicare certe approssimazioni:
 

a) regione lontana, o di "far field", più nota in ottica come regione di Fraunhofer, in cui r è molto grande rispetto alle dimensioni delle sorgenti;

b) regione intermedia, o di "near-far field", altrimenti nota come regione di Fresnel in cui r è grande, sempre rispetto alle suddette dimensioni;

c) regione vicina, o di "near field", in cui r invece è piccolo.

 

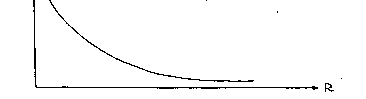
L'approssimazione ora effettuata è quella di Fraunhofer in cui abbiamo lasciato nello sviluppo in serie di Taylor solo i termini che variano secondo 1/r. Dunque nella regione lontana la funzione di Green assume la forma:

con un andamento del tipo riportato in fig. 1.4.

L'eq. 1.11 è costituita da una parte, e^-jkr/(4p r), che rappresenta un'onda sferica partente dall'origine, più un termine correttivo, exp(jkr_0× r'), che tiene conto del fatto che il generico punto di sorgente è in realtà spostato rispetto all'origine stessa (fig. 1.2) e che dipende dalla direzione di osservazione.

b) L'approssimazione successiva (zona b) è quella di Fresnel in cui si considerano anche i termini che variano come 1/r². Si ottiene allora per l'eq. 1.9:

che fornisce la seguente rappresentazione per la funzione di Green:

Rispetto all'approssimazione precedente la struttura è molto cambiata perché il termine aggiuntivo di fase dipende ora da 1/r. Ciò è particolarmente evidente graficando l'eq. 1.13 (fig. 1.5).

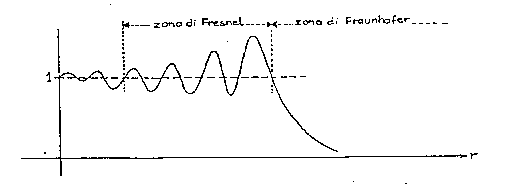
Il diverso andamento riscontrato applicando le due precedenti approssimazioni è alla base delle differenti caratteristiche assunte dal campo elettrico E dato dall'eq. 1.7.

c) La funzione di Green relativa alla regione vicina (zona c) si ottiene facendo approssimazioni di ordine superiore. Questo caso non verrà trattato in dettaglio potendosi estendere facilmente le considerazioni fin qui effettuate. Ovviamente le struttura del campo si complica notevolmente a causa del fatto che tale regione è relativa alle immediate vicinanze dell'antenna dove assumono particolare rilevanza fenomeni di diffrazione.

Naturalmente queste note a carattere essenzialmente qualitativo sono suscettibili di traduzione in termini analitici. In particolare la distanza che definisce il passaggio da zona di Fresnel a zona di campo lontano è legata alle dimensioni dell'antenna a ed alla lunghezza d'onda (quindi alla frequenza) secondo la relazione:

ottenuta considerando gli effetti delle approssimazioni sulla variazione di fase del campo.

Ad esempio, considerando un'antenna di 1 m di diametro e che lavori ad una frequenza di 10 GHz, si ha
 

Per cui a 17 m dall'antenna possiamo considerarci in campo lontano.

 
Fronte d'onda nelle varie regioni
 
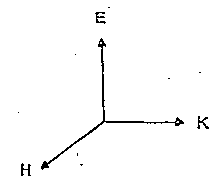
Accenniamo brevemente alla forma assunta dal campo e.m. alle varie distanze dalla sorgente. Come è stato precedentemente evidenziato, nella regione lontana il campo si propaga come una onda sferica che localmente può essere ben approssimata da un'onda piana, per cui il campo deve presentare le caratteristiche tipiche delle onde piane uniformi. E ed H sono in fase temporale, il loro rapporto vale h (h =Ö (m /e ) impedenza intrinseca del mezzo), e sono ortogonali tra loro e rispetto alla direzione di propagazione (fig. 1.6).

Chiaramente, il termine di fase aggiuntivo nella approssimazione di Fresnel non permette di effettuare le stesse considerazioni come ampiamente dimostrato dalla presenza di oscillazioni fino ad una focalizzazione dell'energia nell'andamento del campo.
 

Andamento della potenza

In questo breve richiamo dei concetti della teoria delle antenne, abbiamo preso come grandezza descrittiva delle varie regioni il campo (elettrico o magnetico) nella sua espressione mediante la funzione di Green. Una descrizione alternativa può essere effettuata anche facendo considerazioni sulla potenza, legata al campo - come è noto - mediante il vettore di Poynting complesso:

espresso come fasore per il caso di grandezze di eccitazione sinusoidali. Ovviamente, il flusso di energia in campo lontano è reale ed interamente nella direzione radiale. L'energia è perciò radiata ed il termine "campo di radiazione" è sinonimo di "campo lontano". Da quanto detto nei precedenti paragrafi, si deduce che in campo lontano l'intensità dell'energia radiata decresce come 1/r² con l'aumento della distanza. E' importante calcolare il valor medio del flusso di potenza. Il valor medio temporale del prodotto di due sinusoidi isofrequenziali ed in fase è uguale alla metà del prodotto delle loro ampiezze mentre il flusso totale di energia uscente è uguale all'integrale superficiale del vettore di Poynting su una superficie che circondi completamente l'antenna:
 

In campo vicino, i termini che variano con 1/r³ corrispondono esattamente al campo di un dipolo elettrostatico oscillante; questi termini 1/r³ sono considerati come "campi elettrostatici". I termini che variano con 1/r² sono invece i campi che si sarebbero ottenuti mediante una applicazione diretta della legge di Ampère. Così, il campo rappresentato con il termine 1/r² è detto "campo di induzione" e diventa predominante nei punti intorno all'antenna.

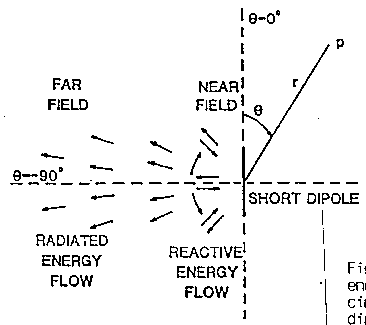
Se si considera il vettore di Poynting risulterà chiaro che i termini elettrostatico e di induzione contribuiscono all'energia che viene immagazzinata nel campo durante un quarto di ciclo e riportata al dipolo durante il successivo senza alcun flusso totale o medio (uscente) all'esterno. In campo vicino il flusso di energia è fortemente reattivo; solo i termini 1/r contribuiscono al flusso di energia medio uscente. Le caratteristiche del trasferimento di energia sono illustrate in fig. 1.7 dove le frecce rappresentano la direzione del flusso di energia in istanti di tempo successivi.

La densità di potenza in campo vicino non è definita univocamente come in campo lontano, dato che i campi elettrico e magnetico ed il loro rapporto variano da punto a punto. Inoltre, la distribuzione angolare è adesso dipendente dalla distanza dall'antenna. E' necessario perciò giungere caso per caso ad una stima quantitativa della densità di potenza anche lungo l'asse. In generale, la densità di potenza in campo vicino dipende dalla forma dell'antenna e dalla distribuzione di campo sull'apertura.
Da notare come queste considerazioni non tengano conto dell'effetto della riflessione con il terreno che potrebbe causare un valore di densità di potenza fino a quattro volte il corrispondente nello spazio libero. E' importante inoltre osservare che la radiazione è largamente confinata entro un cilindro la cui sezione corrisponde all'apertura della antenna fino a che la distanza dall'antenna si avvicina alla regione di transizione. Questo andamento è anche evidenziato dalla densità di potenza lungo l'asse, la quale a grandi distanze varia inversamente con il quadrato della distanza ma in campo vicino oscilla intorno ad un valore costante.

 
Configurazioni tipiche

Concludiamo riportando le configurazioni più comuni in cui possono essere classificate le antenne. Occorre notare però che le antenne sono costruite e si comportano in modo diverso al variare della frequenza impiegata nella trasmissione. Di solito non si impiegano frequenze molto basse, poiché ad un certo punto la teoria delle antenne si confonde con la teoria delle linee di trasmissione.

E' importante per gli scopi del corso accennare a due teoremi che sono alla base del progetto delle antenne.

1. Teorema di reciprocità: un'antenna può operare equivalentemente in trasmissione ed in ricezione mantenendo le stesse caratteristiche.
2. Teorema di similitudine: per antenne che operano a diverse frequenze si possono mantenere le stesse proprietà e.m. purché resti costante il rapporto tra la dimensione geometrica più grande e la lunghezza d'onda. Si effettua cioè una scalatura.(Da notare che qualora l'antenna presenti delle perdite, sarebbe molto difficile scalare rispetto alle dimensioni. In tal caso occorrerebbe modificare contemporaneamente anche il mezzo ma ciò esula dalle condizioni ideali in cui supponiamo di porci.)

- antenne con conduttore lineare od a dipolo (fig. 1.8, a¸ d);

- antenne a guida d'onda od a tromba (fig. 1.8, e-f);

- antenne di tipo ottico od a riflettore (fig. 1.8, g-h).

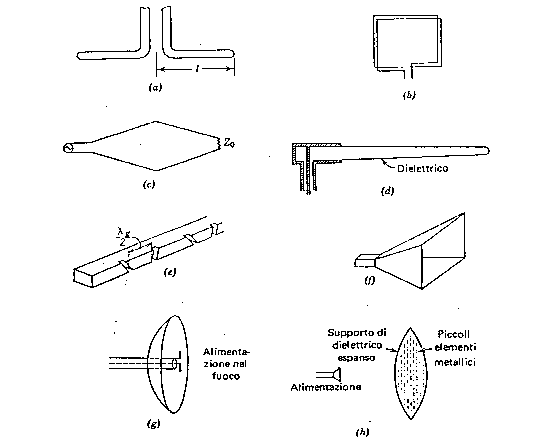
Le ultime due possono essere riunite a costituire le "antenne ad apertura" (quadrata o circolare).

Infine, secondo la più recente teoria degli allineamenti, è possibile riunire due o più antenne con lo scopo (ovvio) di migliorarne le caratteristiche. Nascono così gli "array di antenne" (tipica è la "Yagi" - cioè l'antenna televisiva - costituita da un allineamento di dipoli) di cui è bene conoscerne l'esistenza anche se in questo contesto possono ben essere trattati come un'unica sorgente.

Rimandiamo infine per una trattazione più completa a:
 

- Ramo-Whinnery, "Campi ed onde nell'elettronica per telecomunicazioni", ed. Franco Angeli;

- Collin, "Antennas and radiowave propagation", ed. McGraw-Hill.

- "EST, Enciclopedia della Scienza e della Tecnica", ed. Mondadori, vol. 2, voce "Antenna";
- Appunti del corso di antenne, tenuto dal prof. D'Auria in questa stessa facoltà.    HOME PAGE