In esse è evidente che per w quasi
nullo, i due campi sono indipendenti l'uno dall'altro.
Da notare che il campo puó risultare variabile anche se in realtà
è statico poiché puó essere cheil soggetto esposto
sia in moto!
Campi elettrici in continua ed in bassa frequenza
Assumendo che i due materiali illustrati schematicamente in fig. 2.1 siano caratterizzati, rispettivamente, dalle conducibilità s1 e s2 e dalle costanti dielettriche e1 ed e2, indichiamo le componenti del campo E parallele alla superficie di separazione con E|| e le componenti perpendicolari a detta superficie con E^.
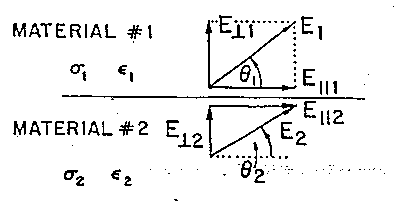
Per i campi sia statici che variabili nel tempo abbiamo:
mentre per i campi statici (DC)
come conseguenza dell'equazione di continuità della corrente
(o della conservazione della carica).
Le orientazioni dei campi totali E nei mezzi 1 e 2 possono essere rappresentate
dalle tangenti degli angoli compresi tra i campi totali e la superficie
di separazione:
Da queste equazioni segue che:
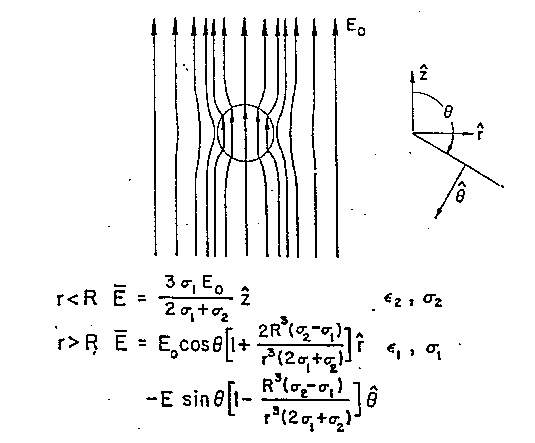
Se il mezzo indicato con "materiale 1" è l'aria con conducibilità s1=10-13 S/m ed il mezzo indicato con "materiale 2" è un tipico tessuto organico con s2 @10-1 S/m, allora risulta tgq1=1012 tgq2 e perciò anche se il campo nel mezzo 2 (campo interno) è quasi parallelo alla superficie di separazione così che q2@0.5º o tgq2@(1/100),risulterá tgq1=1010 o q1=(p/2)-10-10 radianti. Così un campo elettrostatico nell'aria sulla superficie di separazione tra l'aria e tessuto organico, deve essere praticamente perpendicolare a tale superficie.
La situazione alle ELF (Extremely Low Frequencies) è virtualmente la stessa sebbene l'eq. 2.2 debba essere sostituita dalle:
che fornisce a 60 Hz con s2=10-1 S/m, s1=10-13 S/m, e2@10-5F/m ed e1@10-11F/m
Questo risultato, insieme con le eqq. 2.1 e 2.3, mostra che per le proprietà
assegnate del materiale il campo nell'aria deve essere ancora praticamente
perpendicolare alla superficie di separazione con un organismo vivente:
tgq1@2.5*107tgq2.
Dunque, sapendo che l'organismo vivente altererà il campo E
nelle sue vicinanze in modo che il campo esterno sia approssimativamente
perpendicolare alla superficie di separazione, possiamo calcolare direttamente
il campo interno sostituendo il campo totale con il campo perpendicolare
nell'eq. 2.2 (DC) e nell'eq. 2.7 (ELF).
Per i parametri tipici del materiale dato troviamo nel caso statico
(DC) ed a 60 Hz rispettivamente
Dato che la permeabilità magnetica m della maggior parte dei materiali biologici è praticamente uguale alla permeabilità magnetica m0 dello spazio libero, 4p10-7H/m, il campo magnetico statico ed alle ELF "interno" sarà praticamente uguale al campo magnetico "esterno". Le sole eccezioni sono gli organismi come i "batteri magnetosensibili" i quali sintetizzano un materiale ferromagnetico.
La densità di carica superficiale è:
I meccanismi di interazione noti e proposti dei campi magnetici statici con materia vivente sono:
2) Orientazione delle molecole anisotrope diamagnetiche o paramagnetiche e/o elementi cellulari.
3) Generazione di differenze di potenziale ortogonalmente ad una corrente di ioni in movimento (effetto Hall) come risultato della forza magnetica Fm =qvB sinq dove q=carica elettrica, v=velocità della carica, B=densità di flusso magnetico e sinq =seno dell'angolo q tra le direzioni di v e B. Un risultato ben documentato di questo meccanismo è uno "spike" nell'elettrocardiogramma dei vertebrati soggetti a campi magnetici statici elevati.
4) Variazioni nei prodotti intermedi o negli arrangiamenti strutturali nel corso della reazione chimica indotta dalla luce (trasferimento di elettroni), arrecata dallo "splitting di Zeeman" dei livelli di energia della molecola o dagli effetti sulla struttura iperfina. [L'effetto Zeeman consiste nella separazione in più componenti delle linee spettrali, caratteristico delle transizioni elettroniche, sotto l'influenza di un campo esterno H; lo splitting iperfine delle linee di transizione elettroniche in assenza di un campo esterno H è dovuto al momento magnetico del nucleo; così lo splitting iperfine può essere modificato da un campo esterno H applicato]. Le densità di flusso magnetico sviluppate dipendono dal particolare sistema e possono essere elevate fino a 2000 G ma anche minori di 100 G [1 G=10-4W/m²=10-4T]. Le fotosintesi dei batteri e gli effetti sul sistema visivo sono i principali candidati per questo meccanismo.
5) Induzione dei campi E che causano differenze di potenziale elettrico e correnti entro un organismo mediante un rapido movimento attraverso un campo statico H elevato. Alcuni fosfeni magnetici sono dovuti a questo movimento.
dove E è il campo E indotto. L'integrazione è effettuata sull'appropriato percorso di conduzione ed il prodotto scalare con l'elemento di superficie ds indica che solo la componente di ¶B/¶t perpendicolare alla superficie (cioè parallela alla direzione del vettore ds) chiusa dal cammino di conduzione, induce il campo E. Per ottenere un'indicazione dell'ordine di grandezza della corrente indotta che ci si può aspettare come risultato di un campo H alle ELF, consideriamo il percorso circolare di raggio r, illustrato in fig. 2.3.
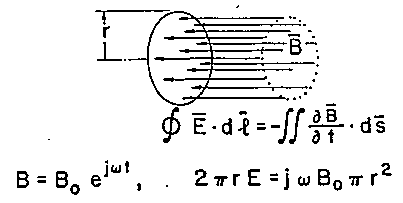
ove w=2pf ed f=frequenza.
L'ampiezza della densità di corrente elettrica risultante J
in Ampère per metro quadrato è:
ove s è la conducibilità lungo
il percorso data in Siemens per metro. Secondo il Sistema Internazionale,
B è misurato in tesla ed r in metri.
Scegliendo per esempio un percorso circolare di 0.1 m di raggio, una
frequenza di 60 Hz ed una conducibilità di 0.1 S/m, dalle eqq. 2.12
e 2.13 si ricava E=18.85 B e J=1.885 B. La densità di flusso magnetico
richiesta per ottenere una densità di corrente potenzialmente significativa
dal punto di vista fisiologico di 1 mA/m² è 0.53 mT ossia circa
5 G. Il campo E indotto da questa densità di flusso lungo un percorso
circolare è di 10 mV/m. Per produrre questi stessi 10 mV/m di campo
E interno da un campo E esterno a 60 Hz occorrerebbe, dall'eq. 2.10, un'intensità
di campo di 250 kV/m! (fig. 2.4).
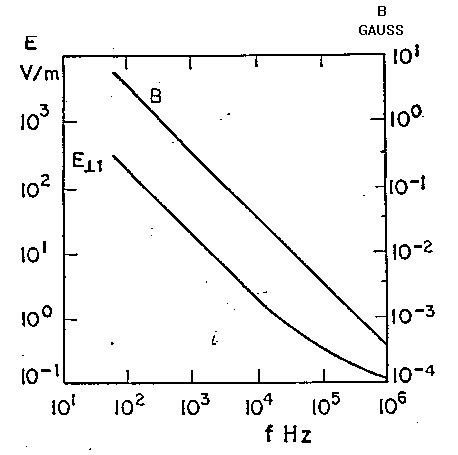
Entrambi i campi E ed H decrescono esponenzialmente con la distanza dalla superficie di separazione
dove g(z) è il campo alla distanza z ed A è l'intensità
del campo immediatamente "all'interno" del contorno.
Come definito dall'eq. 2.14 la profondità di penetrazione d
è la distanza alla quale il campo decresce di 1/e (=0.368) del suo
valore entro la superficie. [A causa della riflessione, il campo A all'interno
del contorno può già essere molto più piccolo del
campo esterno incidente].
L'espressione per d data precedentemente
è stata ricavata per superfici di separazione piane tra mezzi infiniti.
Essa è sufficientemente valida anche per le strutture cilindriche
se il raggio di curvatura rispetto alla profondità di penetrazione
(r0/d) è maggiore di 5 circa.
Per un buon conduttore
Poiché per la maggior parte dei materiali biologici p è dell'ordine di 1 (0.1<p<10) su un range di frequenza molto ampio, è spesso necessario usare l'espressione più generale
La diminuzione dell'intensità del campo con la distanza dalla
superficie di contorno indicata dall'eq. 2.14, diventa significativa per
molti tessuti biologici alle frequenze ove r0/d>5
non è soddisfatta. Tuttavia, l'errore risultante dall'uso delle
eqq. 2.14 e 2.15 o 2.17 con oggetti curvi è minore quando z<d;
così per z=0.693d, dove g(z)=0.5 A dalle
eqq. 2.14 e 2.15, il corretto valore di g(z) ottenuto risolvendo l'equazione
delle onde in coordinate cilindriche differisce solo del 20% (è
0.6 A) anche quando r0/d è
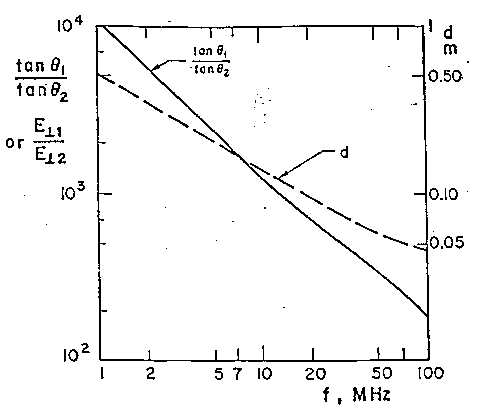
molto piccolo. Perciò in fig. 2.5 è riportata la distanza
d=0.693d, invece che d,
alla quale il campo decresce fino a metà del suo valore all'interno
della superficie di separazione per il range di frequenza 1÷100
MHz, usando l'eq. 2.17 con i tipici valori per s
ed e per il muscolo. E' evidente che l'effetto
pelle diventa significativo per gli uomini ed i vertebrati più grandi
a frequenze >10 MHz.
Direttamente collegato alla profondità di penetrazione, che è
definita per campi variabili sinusoidalmente con il tempo, è il
fatto che una rapida variazione del transitorio di una densità di
flusso magnetico applicata costituisce un'eccezione alla dichiarazione
che un campo H in continua entro la superficie di separazione è
uguale al campo H esterno. Così, da un certo punto di vista si può
considerare la rapida applicazione o rimozione di un campo H in continua
come fosse equivalente all'applicare un campo ad alta frequenza durante
il periodo di switching, essendo le frequenze più alte presenti
dell'ordine di 1/t dove t
è il tempo di risalita della funzione gradino applicata. Così,
se t<10-8sec, l'effetto pelle
sarà importante durante il periodo di transizione giacché
d in fig. 2.5 è minore di 5 cm su 100 Mhz.
E' anche possibile calcolare direttamente la densità di flusso
magnetico entro un cilindro conduttore come funzione della posizione radiale
r e del tempo t quando viene applicato un impulso magnetico nella direzione
assiale. Assumendo nullo il tempo di salita del campo applicato B0,
cioè una vera funzione gradino, si trova che il campo all'interno
del cilindro di raggio a è:
ove J0(rnk/a) è la funzione di Bessel di ordine 0 di argomento rnk/a , la sommatoria è fatta sugli zeri di J0 chiamati nk (i primi quattro valori di nk sono 2.405, 5.520, 8.654 e 11.792) e tk è il tempo di risalita del k-esimo termine della serie ed è dato da:
Se nk cresce, allora il tempo di salita diminuisce e perciò il ritardo più lungo è dovuto al primo termine nella sommatoria con k=1:
Per un cilindro di 0.1 m di raggio e con una conducibilità s@1 S/m che è un valore tipico per il muscolo tra 100 e 1000 Mhz, l'eq. 2.20 dà t1 =2.6·10-8sec. Questo tempo di salita finito (o tempo di decadimento nel caso di campo rimosso) del campo H interno può avere una qualche importanza quando i campi H impulsivi sono usati terapeuticamente. Potrebbe anche essere usato per misurare in modo non invasivo la conducibilità delle sostanze biologiche in vivo, attraverso la determinazione della velocità di decadimento finale del voltaggio indotto, in una spira di prova dal campo interno lentamente decadente dopo che il campo applicato è stato rimosso.
La perdita per riflessione sulla superficie di un organismo è
una conseguenza della differenza tra le sue proprietà elettriche
e quelle dell'aria. Ogni qualvolta un'onda e.m. viaggia da un materiale
ad un altro con proprietà elettriche diverse, le condizioni al contorno
(eqq. 2.1 e 2.6 e relazioni simili per il campo H) richiedono l'esistenza
di una onda riflessa.
Le espressioni per il coefficiente di riflessione
ed il coefficiente di trasmissione
diventano piuttosto semplici per dielettrici senza perdite (p«1)
e per buoni conduttori (p»1). Poiché le sostanze biologiche
non sono né l'uno né l'altro, sono necessarie le espressioni
più generali per G e T, applicabili alla
superficie piana.
Per incidenza perpendicolare, illustrata in fig. 2.6, si ha:
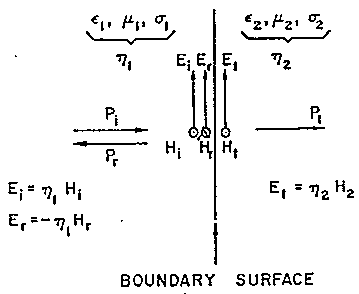
Chiaramente G e T sono in generale numeri complessi, anche quando il mezzo 1 è l'aria per la quale l'eq. 2.25 si riduce alla quantità reale h0=n(m0/e0) poiché il mezzo 2, che qui è la materia vivente, usualmente ha un'impedenza d'onda complessa alle RF.
Le potenze incidente, riflessa e trasmessa sono date da:
dove i campi E sono valori efficaci (Eeff = [Emax/2]-1/2) di quantità sinusoidali, Re si riferisce alla "parte reale di...", h* è il complesso coniugato di h ed R1 ed R2 sono le parti reali di h1 ed h2. Se il mezzo 1 è l'aria, h1=R1=377W. Segue dalle eqq. 2.21, 2.22 e 2.26÷2.28 e dalla conservazione dell'energia che il rapporto tra la potenza reale trasmessa e quella incidente è dato da:

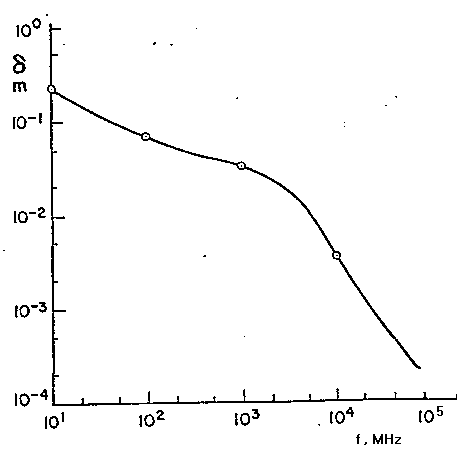
In fig. 2.8 è mostrata la frazione della potenza totale incidente
che viene trasmessa, evidenziando che la perdita per riflessione all'interfaccia
decresce con la frequenza. Tuttavia, per un tessuto situato più
internamente questo effetto è controbilanciato dal fatto che anche
la profondità di penetrazione d (eq.
2.17) decresce con la frequenza (fig. 2.9) cosicché la potenza totale
penetrante entro la superficie decresce rapidamente.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
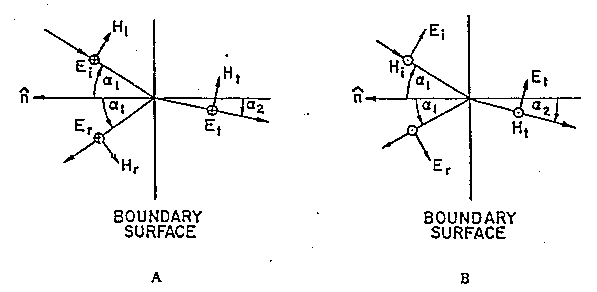
I coefficienti di trasmissione e di riflessione sono differenti per i due tipi di polarizzazione e diventano anche funzioni dell'angolo di incidenza a1:
così che cos a2 =[1-sin2
a2 ]1/2 è
un numero complesso a meno che p2 =(s/we2)«1.
Come esempio è mostrata in fig. 2.11 la variazione con l'angolo
di incidenza a 10 MHz del coefficiente di trasmissione per la polarizzazione
perpendicolare all'interfaccia aria-muscolo. E' evidente che in questo
caso il campo trasmesso non necessariamente è massimizzato dall'incidenza
perpendicolare. Inoltre, ogniqualvolta p@1 o
p>1 (vedi tab. 2.1) a2 è complesso
e ciò causa che l'onda entrante nel tessuto sia non omogenea. [Ci
sono onde piane non semplici, cioè onde ove le superfici equifase
ed equiampiezza non coincidono; solo i piani equiampiezza sono paralleli
alla superficie di separazione].
Rimandiamo comunque per ulteriori approfondimenti al testo da cui è stata tratta questa parte: