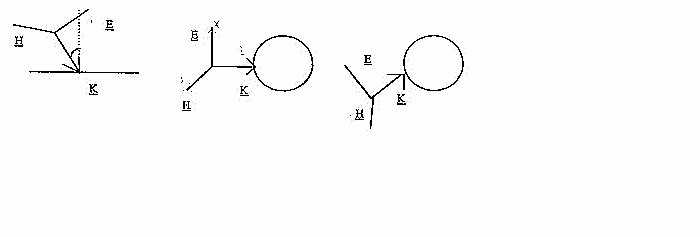
MODELLO SFERICO OMOGENEO
Approssimando un corpo ad un piano indefinito si ha che l'onda
che penetra in esso viene a dipendere
dall'angolo d'incidenza con cui l'onda ( localmente piana) incide
su tale piano.
Se si approssima il corpo ad una sfera, tale dipendenza viene a
cadere, o meglio, si sposta il problema
dalla dipendenza dell'angolo d'incidenza all'orientazione dei
vettori del campo. In una struttura sferica,
da qualunque parte si incida la superficie ho sempre uno dei tre
vettori E,H,K (a seconda dell'orientazione)
che va al centro della sfera. Ruotare la sfera o ruotare il campo
lascia il problema invariato a meno di una
traslazione del campo .
II problema di un onda incidente (1) una sfera nel vuoto e un
noto problema di scattering risolto nel l941 da
Stratton, con la soluzione di Stratton posso trovare il campo
e.m. all'interno della sfera che verifica le condizioni
al contorno.
Tale soluzione è una "serie" di espressioni di vettori
sferici (2).
Tali espressioni saranno mostrate con dei coefficienti ricavabili
attraverso le caratteristiche del C.E.M. Quindi il campo
all'interno di una sfera di materiale omogeneo è:
(1) Consideriamo un onda che si propaga lungo l'asse z, i campi E,H sono polarizzati linearmente lungo gli assi:
 |
 |
(2) Stiamo facendo questo per
trovare informazioni più specifiche su quello che succede ad un
soggetto esposto ad una certa distanza da un
trasmettitore
(campo lontano). La sfera è un modo più elegante del piano (o
slab) per simulare un corpo umano.
Inserendo 1'equazione del campo in un elaboratore è
possibile calcolarlo noti i valori numerici della
permittività e la conducibilità del materiale.
All'interno della sfera una parte del campo sarà
trasmessa, una parte scatterata e per la
conservazione dell'energia la differenza sarà assorbita.
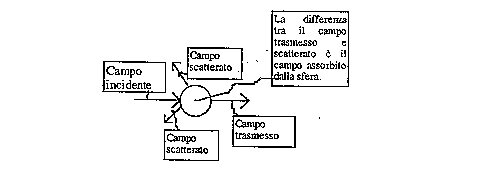
Ragionando in termini di potenza:
con: Wa pot. Assorbita,Wt pot.trasmessa.Ws pot. Scatterata.
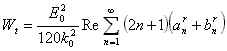
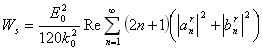
in cui i coefficienti sono dati da:
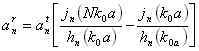
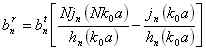
dove:
.
é la costante di propagazione.
a raggio della sfera
sono
rispettivamente la permittività e la lunghezza d'onda nel vuoto.
Quindi tutte queste grandezze sono funzioni della lunghezza
d'onda, della costante dielettrica, della permittività e della
dimensione della sfera.
Per calcolare la potenza assorbita dalla sfera si procede al:
1- calcolo dei coefficienti 
che sono delle funzioni di Hankel le quali sono la
differenza di funzioni di Bessel
dipendenti dal raggio della sfera.
2 - alla valutazione di tali coefficienti in 
3- al calcolo di 
.
 |