ANALISI
SULLA DISTRIBUZIONE DI CAMPO ALL'INTERNO
DI UN CORPO SFERICO INVESTITO DA UN'ONDA ELETTROMAGNETICA
Si considera un corpo sferico omogeneo nei parametri
elettromagnetici.
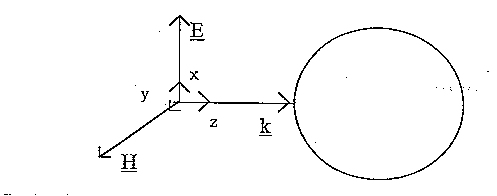
Si vuole analizzare il campo distribuito all'interno del corpo
Si analizza il cervello che ha una densità di massa circa uguale
ad uno (le variazioni sono del 5- 6%)
- Si fissa la frequenza a 918MHZ (che successivamente e
diventata prossima alle frequenze dei telefoni cellulari)
- Si fissa il materiale: il cervello
- Si normalizza alla potenza di 1mW/cm' (densità di
potenza incidente)
- Si analizzano gli andamenti lungo gli assi x,y,z, poiché
e difficile graficare una densità d'i potenza in 3D
- Si varia il raggio della sfera:
r =3cm, r =5cm, r = 7cm, r = 9cm (dimensioni della testa
di topi, gatti, cani e uomini).
I risultati sperimentali ottenuti utilizzando il modello
sferico sono graficati di seguito
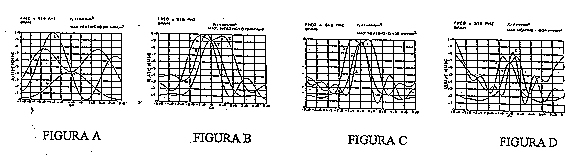
Effettuando un'analisi di massima si osserva che:
- Massimo riscaldamento locale all'interno del materiale
della singola componente: il massimo e quasi sempre
lungo l’asse di propagazione z (potrei vedere la
sfera come una successioni di slab)
- Per le.figure A,B,C il massimo non e sulla superficie
della sfera; in B e in C i punti più caldi sono al
centro della sfera.
- Il fenomeno più interessante si ha per la figura D: il
massimo e sulla superficie della sfera in particolare per
le
componenti x,z. Ciò e dovuto al fatto che se la sfera e
sufficientemente lunga avrò un decremento del campo
(come accade per uno slab) man mano che il campo penetra.
Interessante e osservare che ci sono dei valori di
potenza elevati anche dalla parte opposta rispetto a dove
l'onda
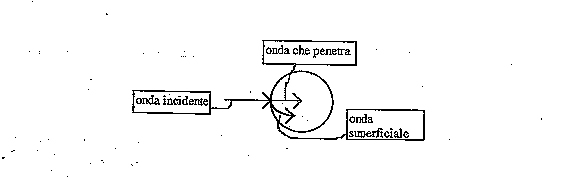
sta incidendo. La spiegazione e che il campo incidendo
sulla sfera crea un'onda superficiale che, viaggiando
all'interfaccia superficie sferica/materiale esterno,
segue il profilo della sfera e si richiude dall'altro
lato della sfera.
Da questo lato della sfera due sono i contributi del
campo uno superficiale ed uno che arriva dall'interno
della sfera
(contributi in fase).
Si passa ora ad analizzare i risultati del modello sferico
andando a leggere il comportamento puntuale.



