ASPETTO LOCALE
![]()
Per comodità si considera la costante dielettrica del cervello pari a 100, ottenendo cosi la lunghezza d'onda nel dielettrico:
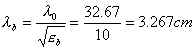
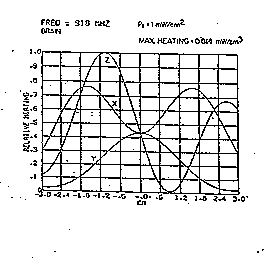 |
figura A la sfera ha le dimensioni della lunghezza d'onda, allora il campo può percorrere tutto il suo periodo spaziale nell'interno della sfera, penetrando anche se comincia ad attenuarsi (notare lungo 1'asse z che ha quasi l'andamento di una lunghezzad'onda). Dall'altra parte della sfera ancorauna volta si ricompongono i due contributi |
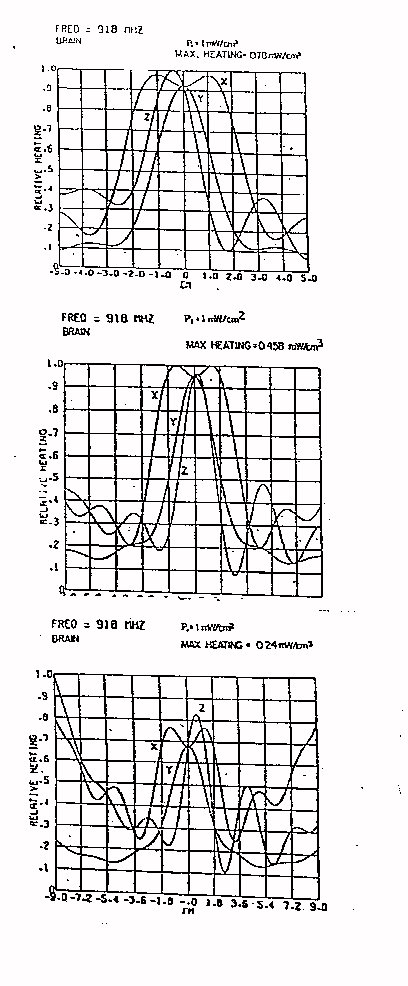 |
figura B,C le sfere hanno le dimensioni circa il doppio della
lunghezza d'onda, si osserva che i fenomeni
d'interferenzacostruttivi dovuti all'onda riflessa si
hanno al centro sella sfera. figura D la sfera e molto più grande della lunghezza d'onda, si nota il fenomeno di attenuazione. |
Tra i diversi casi il massimo di campo e nella sfera piu
piccola, aumentandone le dimensioni il massimo tende a diminuire.
Analizzati i risultati sperimentali dell'assorbimento di campo
per un onda incidente la sfera a frequenza di 918 MHZ, si
analizzerà ora lo stesso esperimento per una frequenza di 2450
MHZ in modo da verificare la presenza di comportamenti variabili
con la frequenza. Variando la frequenza da 918MHz a 2450MHZ la
lunghezza d'onda diventa:
Con f = 2450 MHz si ha:
![]()
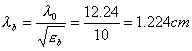
aumentando la frequenza il campo tende a penetrare molto di
più, quindi la potenza all'interno e maggiore a
parità di potenza incidente.
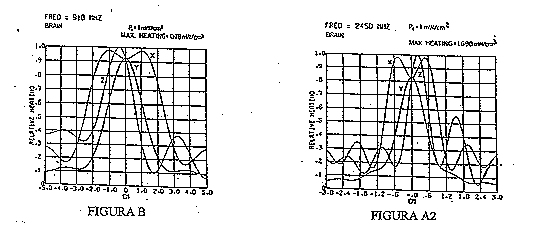
Comparando la figura B(che considera una sfera di 10 cm di
diametro pari alla testa di un gatto) con la figura
A2 ( che considera una sfera di 6 cm di diametro pari alla testa
di un topo) si nota una somiglianza, ciò è perché
i due casi hanno stesso rapporto lunghezza d'onda/ dimensione
sfera. E' quindi il rapporto tra X e il diametro
che influenza la distribuzione di campo.
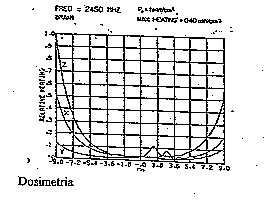 |
figura D2 Il fenomeno di attenuazione è nettissimo |
Aumentando le dimensioni della sfera aumenta il fenomeno di
addensamento del campo sulla superficie d'ingresso
della sfera salvo fenomeni di ricombinazione in fase al centro. I
risultati visti finora evidenziano che a seconda
delle dimensioni del soggetto si avranno delle situazioni di
assorbimento di picco (in risonanza) a ben determinate
frequenze (l'affermazione di questa frase e valida anche
leggendola al contrario).
Le dimensioni del soggetto sono critiche rispetto alle condizioni
di assorbimento, il soggetto può assorbire di più
o di meno rispetto alla frequenza considerata. L'assorbimento non
e costante su tutto lo spettro ma ci sono delle
frequenze caratteristiche(funzione delle dimensioni
dell'oggetto).
Automaticamente tale risultato (importanza delle dimensioni del
soggetto) mette in crisi il modello sferico come approssimazione
del corpo umano.