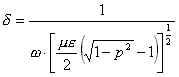
CONCLUSIONI
Riassumendo i risultati dei grafici della sfera alle frequenze 918 MHz e 2450 MHz, si può affermare che:
1) aumentando la frequenza si trasferisce maggiore potenza
all'interno del materiale (la sfera) in quanto
aumenta la penetrazione.
2) aumentando la frequenza la regione di penetrazione del
campo diminuisce riducendosi il valore di d
,
come mostrato dalla seguente relazione
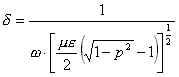
ove d e la distanza in cui il campo
e diminuito ad 1/e del valore all'interfaccia.
Da questa relazione si traggono due aspetti peculiari:
- diminuzione di 5 dovuta all'aumento della frequenza;
- diminuzione di å dovuta all'aumento della a (con l'incremento della frequenza).
3) si hanno fenomeni di risonanza (4).
(4)fenomeno di risonanza
In una cavità chiusa (detta cavità risonante) in cui vengono immesse onde elettromagnetiche si stabilizzano onde stazionarie le cui lunghezze d'onda e configurazioni geometriche sono strettamente correlate alla geometria della cavità. Le dissipazioni dipendono dalle caratteristiche fisiche delle pareti metalliche (Q della cavita).
Per trovare la frequenza di oscillazione si distinguano due casi:
Si ha 
con e ,m indipendenti
da w ,allora:
Si ha:
con
che tiene conto della conducibilità,allora:
dove
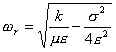
e
L'espressione è complessa perché in un mezzo dissipativo le
oscillazioni libere si attenuano per perdita di
energia. Per s
tendente a zero, 
tende a zero. Nel caso di dissipazioni si hanno
oscillazioni smorzate,
in tal caso viene definito un coefficiente di risonanza detto
fattore di qualità:
e poiché :
si ha:
.
Se si ha una struttura non dispersiva in presenza di oscillazioni smorzate il campo si attenua con legge:
e l'energia media si attenua con legge :
La derivata di tale energia media rappresenta la potenza
dissipata (cambiata di segno perché 1'energia
diminuisce per la dissipazione) allora:
da cui:
allora il fattore di qualità diventa:
.
Finora si sono analizzate sfere di raggio fissato ad
una data frequenza.
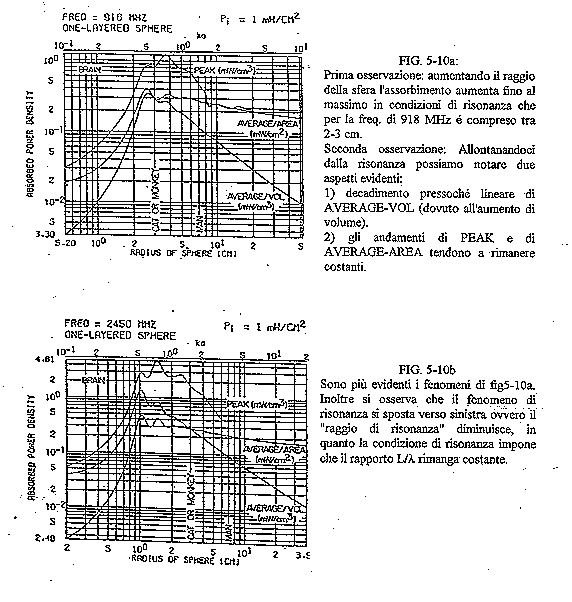
Di seguito si vuole mostrare come vari 1'assorbimento all'interno
di una sfera ad una data frequenza ma su
sfere di raggio diverso.Tutto ciò é mostrato nei grafici
seguenti in cui PEAK é la densità di potenza per
unità di volume all'interno della sfera, AVERAGE-AREA
rappresenta la densità superficiale media di potenza
sulla sezione con superficie massima perpendicolare alla
direzione di propagazione del c.e.m., AVERAGE-VOL
é la densità media di potenza per unita di volume.
 |
 |