DISCRETIZZAZIONE DELLE EQUAZIONI DI MAXWELL²

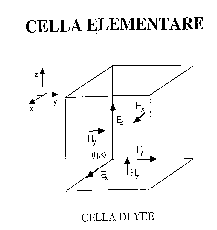
Descritte le equazioni di Maxwell e ricordando la convenzione della cella di Yee si discretizzano le equazioni
differenziali in rapporti incrementali.

² Discretizzazione: data una funzione F delle variabili continue x,y,z,t la corrispondente funzione discretizzata è rappresentata come:

dove i,j,k individuano un punto discreto ed n un istante di tempo discreto, osservando che se discretizzo lo spazio in cubi, d è il lato.

Descritte le equazioni di Maxwell e ricordando la convenzione della cella di YEE si discretizzano le equazioni differenziali in rapporti incrementali, usando un algoritmo alle differenze finite centarate.

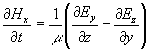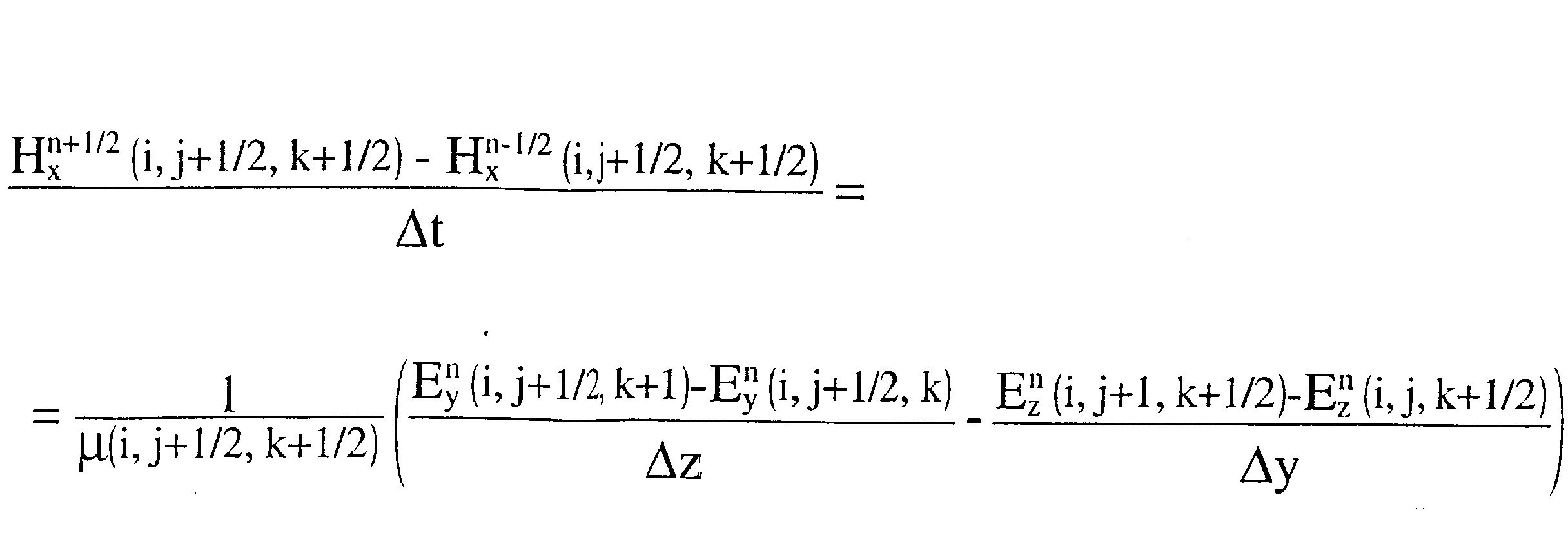
Allora il campo Hx diventa :

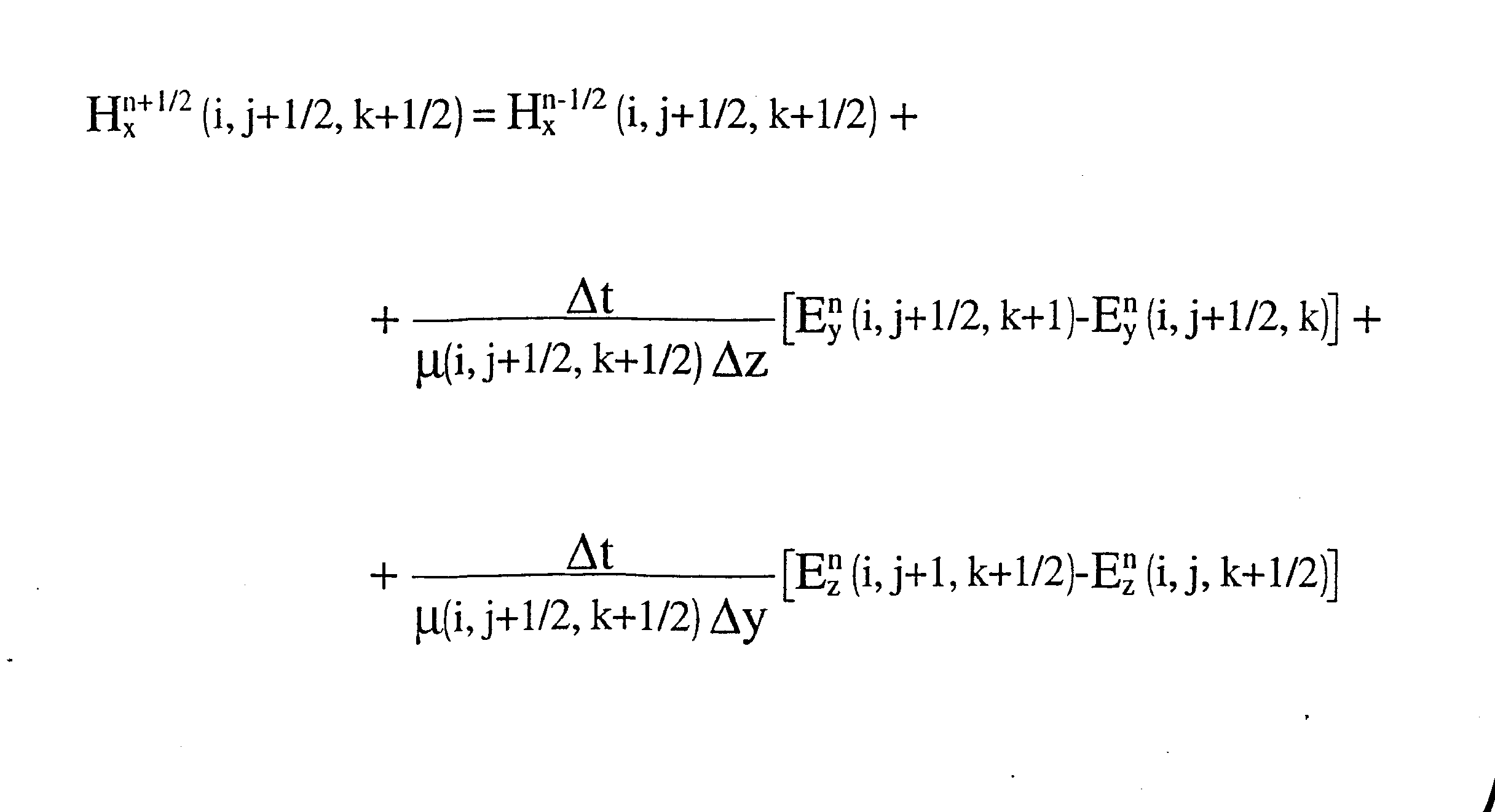
Nell’ implementazione al computer diventa

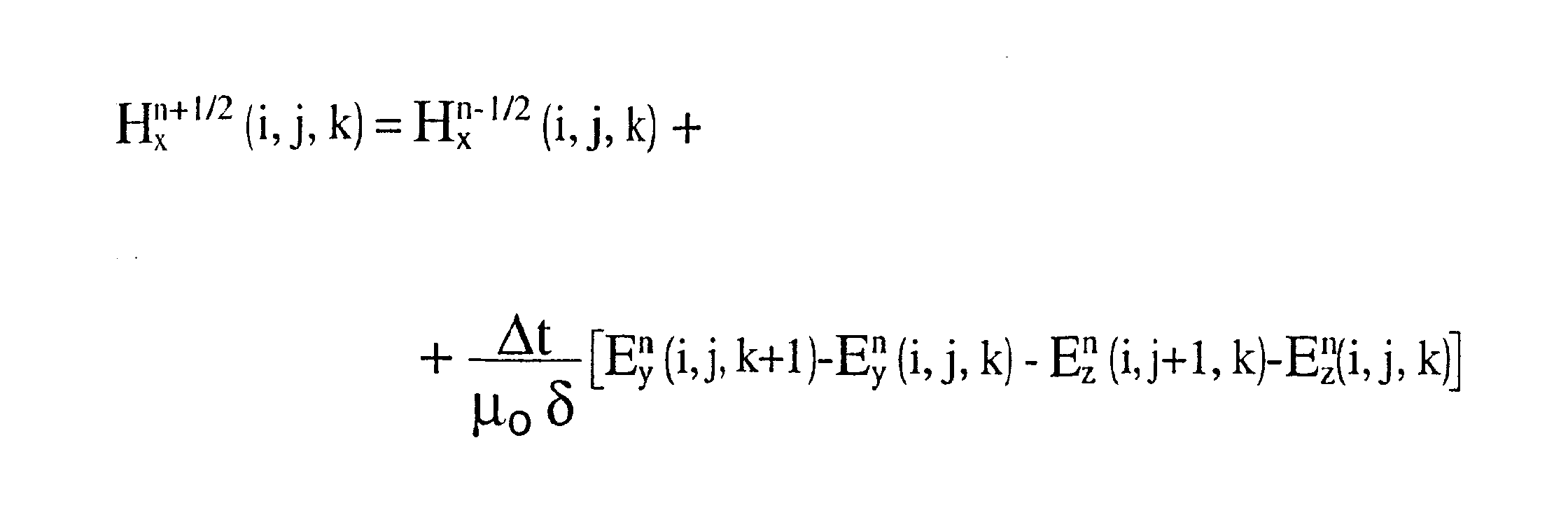
Condizioni importanti del metodo sono la stabilità e l’accuratezza che devono dare una risposta a tali quesiti:

1. Esiste una soluzione ? (stabilità)
   
2. E’ quella che si sta cercando? (accuratezza)

ACCURATEZZA:

Ci dice quanto la soluzione trovata si avvicina a quella vera.

Per avere una soluzione campionata in un numero sufficiente di punti dovrà essere:

Dal teorema di Shannon deriva che per evitare problemi di ‘aliasing’ è necessario scegliere almeno d £ l /2 .

Una scelta di è di solito ritenuta accettabile.

STABILITA’:

La soluzione non varia al crescere del tempo, per esempio, non deve crescere indefinitamente, ciò significa che se:

errore al passo n

deve essere:

Si avrà quindi una condizione che verifichi la stabilità se rispettata. Essa è la seguente:

CONDIZIONI DI STABILITA'

Le equazioni dell'algoritmo di Yee convergono ad una soluzione stabile se:

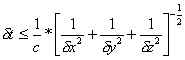
ad esempio con

con

Ovviamente come ogni soluzione numerica tale modo presenterà degli errori.

Questi sono:

- errori del modello (approssimazione della realtà)

- errori di troncamento (dovuti alla discretizzazione)

- errori di roundoff (dovuti alla precisione finita del computer)

Si riporta:

ERRORE CON LA DIMENSIONE DEL PASSO DI GRIGLIA

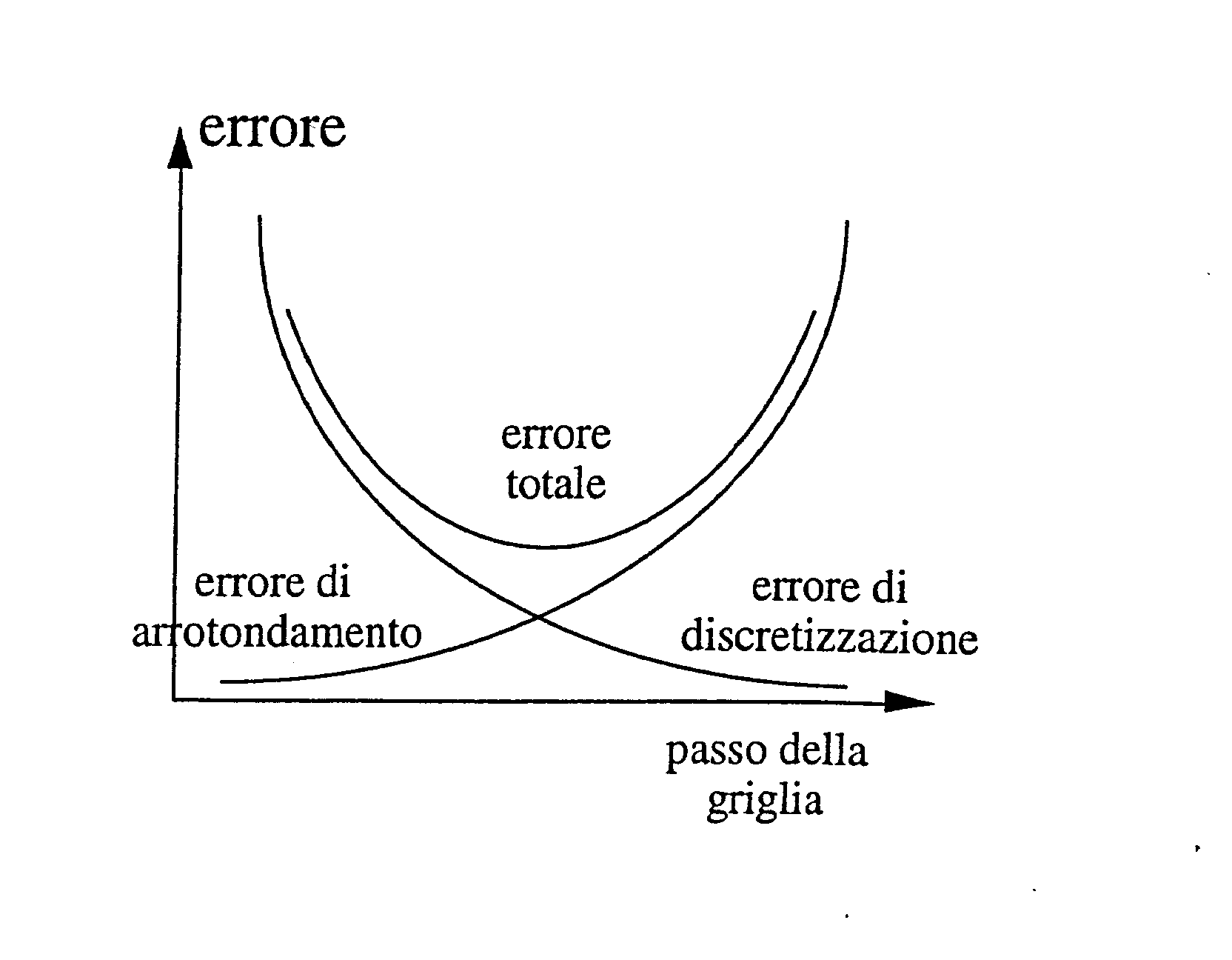
Si nota dagli andamenti degli errori e più in generale dell’errore totale che esiste un punto di ottimo da scegliere per la misura del passo della griglia. Tale punto è nel minimo dell’errore totale.

La discretizzazione dello spazio, oltre a generare degi errori, rende il mezzo dispersivo.
Per lo studio del modello è stato fissato un sistema di assi coordinati XYZ rispetto ai quali è stato campionato lo spazio.
Il campo elettromagnetico si propaga secondo una direzione generica
(vettore di propagazione), che forma rispetto al sistema coordinato un angolo a .
Dalla teoria della propagazione dei C.E.M. , deriva che la velocità di propagazione dell’onda e la relativa velocità di fase possono essere diverse, e la loro differenza dipende dall’angolo a .
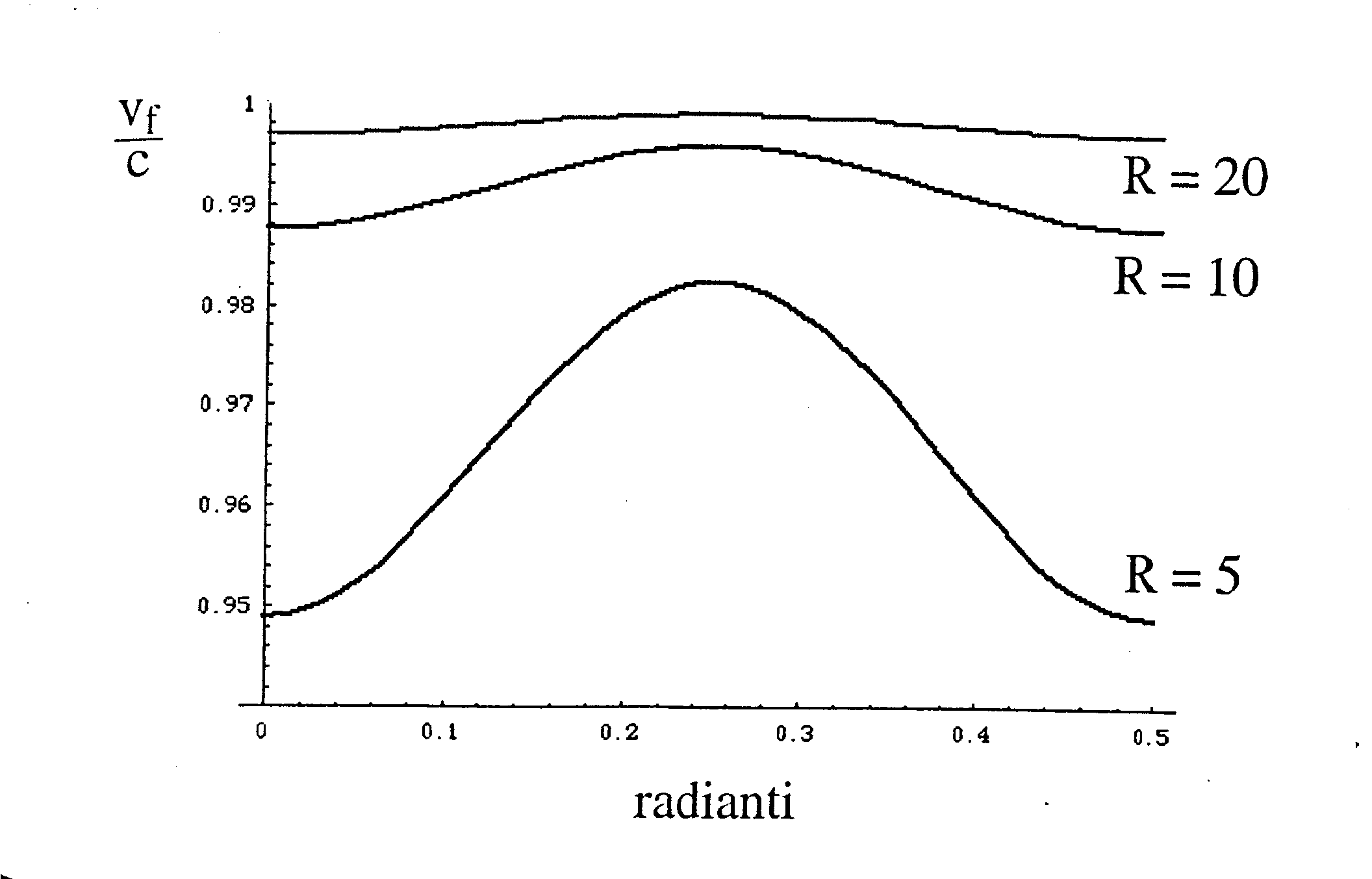
Il modello utilizzato sarà tanto migliore quanto più il rapporto tra la velocità di fase dell’onda (all’interno del materiale) nel modello e quella dell’onda reale nel vuoto tende a 1 al variare di come è rappresentato dal seguente grafico tenendo conto
che tale rapporto oltre che da dipende anche dal parametro (ove è il passo di discretizzazione):
La scelta di R è una seconda specifica da soddisfare nella scelta del passo di campionamento oltre a quella imposta dal teorema di Shannon.

Torna al menu precedente