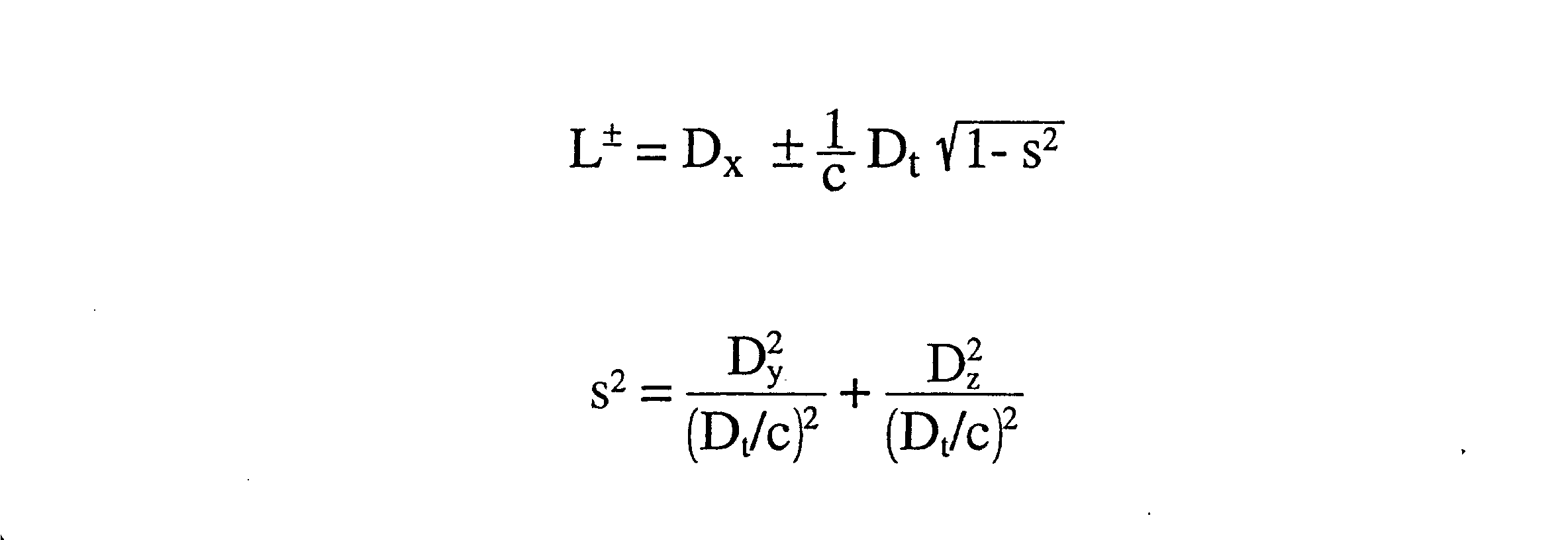
CONDIZIONI DI ASSORBIMENTO
Nello studio del modello si sono considerate condizioni di
propagazione nello spazio libero.
Se delimito le dimensioni di analisi in un certo spazio e non
calcolo le componenti di campo all’esterno è come se
considerassi delle componenti di campo nulle al di fuori dello
spazio di analisi; è l’equivalente di mettere ai bordi del
dominio delle pareti elettriche perfette e quindi avere una
riflessione totale. Dovrò quindi imporre determinate condizioni
al contorno in modo tale da simulare la propagazione nello
spazio libero. Sono queste le condizioni di Mur.(1981)
Dx,Dy,Dz,Dt sono operatori lineari e rappresentano le derivate
parziali rispetto a X,Y,Z,t.
L è un operatore lineare che applicato ad una generica
componente di un campo vettoriale fornisce l'equazione delle onde
(+ sta per onda progressiva o regressiva).
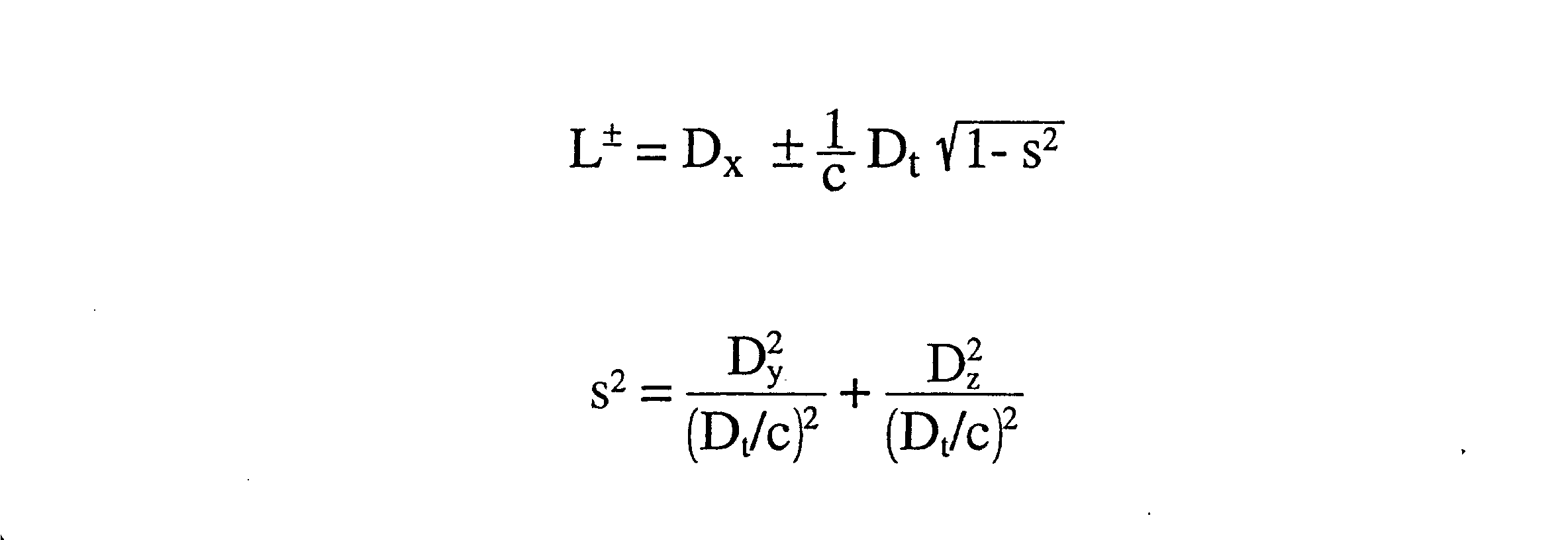
Se:
dove U è la
generica componente del campo.
allora l’equazione dell’onda ha come soluzione
un’onda regressiva. Quindi se si applica l’operatore 
alla funzione U in x=0
non si hanno riflessioni.
Mur 1° ordine:
Mur 2° ordine:
Le situazioni di studio sono prevalentemente tre:
- Campo lontano: approssimazione dell’ onda come localmente piana
- Campo vicino:
a) - dipolo a l /2 alimentato al centro (trasmettitori radio portatili)
b) - telefono cellulare
- Eccitazione in strutture guidanti
I possibili andamenti temporali delle eccitazioni sono:
VANTAGGI FDTD
Uno dei maggiori vantaggi di questo metodo è
l’occupazione di memoria sul computer in quanto è lineare
con il numero delle celle (N) cosa non possibile ad esempio con
il metodo dei momenti in cui l’incremento di memoria con il
numero delle celle è al meglio proporzionale ad NlogN.
In più si possono considerare geometrie comunque complesse con
poche modifiche e la possibilità di considerare sorgenti sia in
campo lontano che in campo vicino (antenne, applicatori per
ipertermia, impianti industriali, ecc.).
SVANTAGGI FDTD
Di contro si hanno i seguenti svantaggi: difficoltà a seguire correttamente i contorni curvilinei in quanto la cella base è a forma cubica, presenza di errori dovuti all’approssimazione per le condizioni di troncamento, attesa di condizioni stazionarie per ottenere i dati di uscita.
APPLICAZIONI NEL BIOELETTROMAGNETISMO
Gli ambiti di applicazione sono distinti in due categorie.
La prima, per la definizione dei livelli di pericolosità
relativi alle normative di sicurezza nelle due situazioni di
campo lontano e campo vicino.
La seconda per scopi terapeutici (monitoraggio per tecniche di
ipertermia o ricalcificazione ossea) e diagnostici.
Un valido esempio di applicazione del metodo FDTD è lo studio
dello scattering da sfera omogenea, per cui è nota la soluzione
analitica esatta che ci permette una verifica del modello.
Nella regione di campo diffusa si applicano le condizioni al
contorno di Mur.
L’esperimento è stato effettuato sotto le seguenti
condizioni:
1) si considera uno spazio di 51x51x51 centimetri cubici,
2) una dimensione della cella di d =3mm,
3) un eccitazione con onda piana uniforme alla frequenza di 2.5 GHz,
4) elemento scatterante una sfera omogenea di raggio 4.5 cm e costanti elettromagnetiche e =4, m =1, s =0.
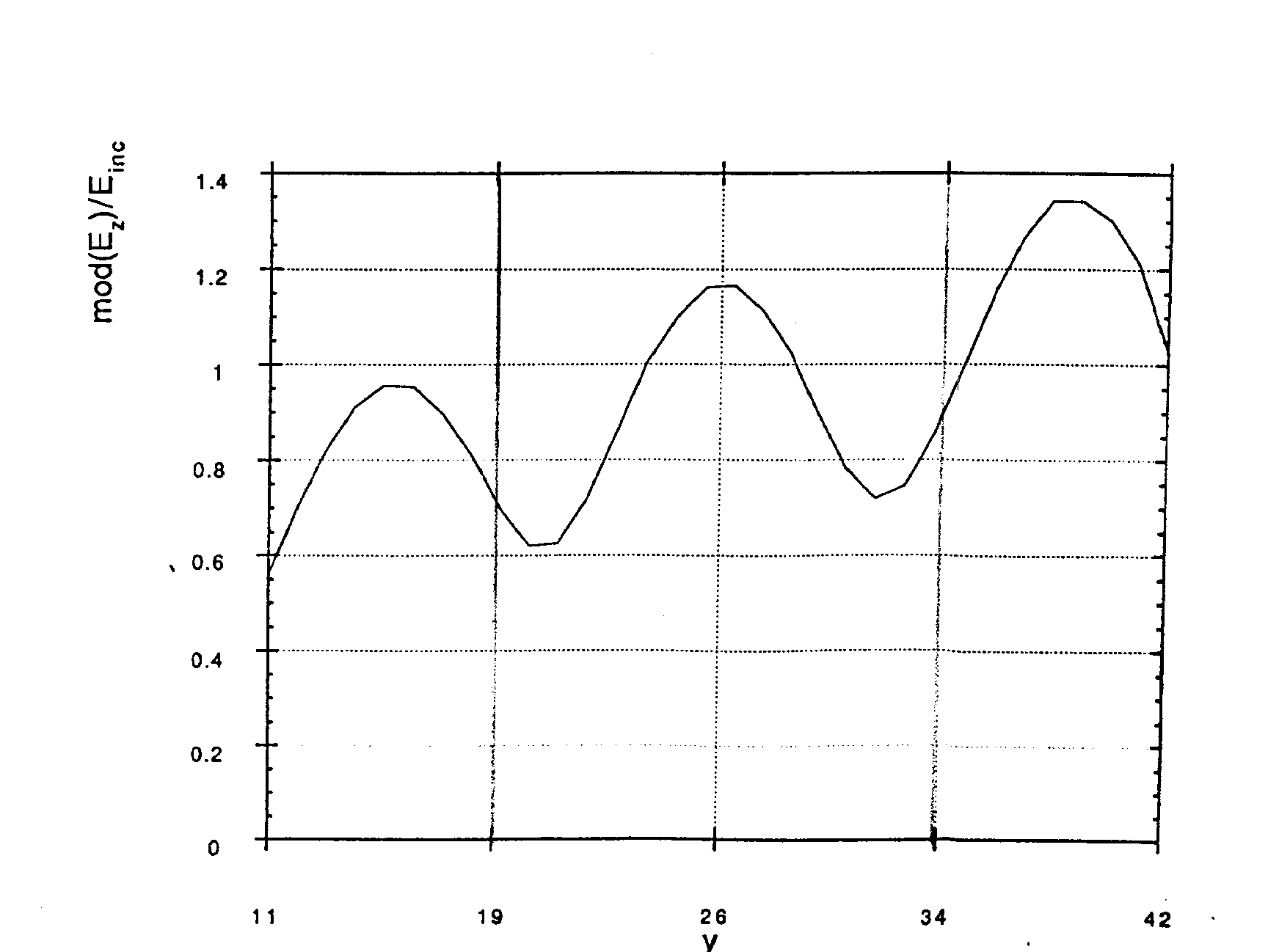
I risultati ottenuti sono descritti dal modulo del campo
elettrico polarizzato lungo z, normalizzato rispetto al campo
incidente. Sull’asse delle ascisse si ha la direzione di
propagazione y.
Si osserva un buon accordo con i risultati analitici sulla sfera
(Pagg. 17-18, Figg. 5.11-5.12).
CORRENTE DI PIEDE
Sempre rimanendo nel caso di esposizione in campo lontano,
possiamo considerare la situazione di esposizione ad un’onda
piana uniforme incidente su un modello di uomo considerato
"omogeneo".
La corrente di piede si definisce come: quella corrente che
fluisce attraverso un’uomo, sottoposto ad un c.e.m., verso
un piano di massa. E’ stata introdotta per la prima volta da
una normativa americana nel 1992
 |