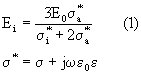
Analisi dell'accoppiamento EM sulla cellula
Le proprietà dielettriche dei tessuti biologici, consentono la diffusione delle onde EM negli esseri viventi, provocando effetti termici e non. Inoltre i campi EM di nostro interesse non riescono a produrre fenomeni di ionizzazione; ne consegue che per poter spiegare gli effetti non termici, si dovranno prevedere meccanismi di amplificazione del campo. Per dimostrare ciò è sufficiente analizzare cosa accade ad una cellula quando è sottoposta ad un segnale EM.
In una prima approssimazione schematizzeremo la cellula con un corpo dielettrico sferico di conducibilità s i e costante dielettrica e i immerso in un mezzo omogeneo con caratteristiche s a e e a, il tutto investito da un campo uniforme E0. Applicando l'equazione di Laplace, valida in condizioni quasi statiche (bassa frequenza), il campo all'interno della sfera risulterà essere dato da :
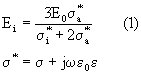
La validità della relazione (1) è confermata dal rispetto dell'ipotesi di costanti concentrate, fino a frequenze comprese tra i 10 ed i 100 GHz; infatti per queste frequenze la lunghezza d'onda è dell'ordine dei mm, cioè di due ordini di grandezza maggiore della dimensione della cellula (" 100 m m), ovvero l >Rsfera .
Se le proprietà dielettriche della sfera fossero quelle di un tessuto con elevato contenuto d'acqua (tessuto soffice) immerso in aria (e aria=e 0) si avrebbe che: ![]() ;
;
![]()
e la densità di corrente interna:
![]()
Si può osservare che se in quest'ultima relazione introducessimo un E0 a 10 Hz ed una ![]() si verrebbe ad avere un campo interno attenuato di sette ordini di grandezza rispetto a quello incidente esternamente sulla cellula.
si verrebbe ad avere un campo interno attenuato di sette ordini di grandezza rispetto a quello incidente esternamente sulla cellula.
Possiamo quindi affermare, nel caso di accoppiamento in aria che:
Il discorso si riporta parimenti qualora avessimo modellizzato la cellula invece che con una sfera omogenea con un ellissoide omogeneo.
Accoppiamento EM sulla membrana
A livello biologico la cellula sappiamo essere costituita: esternamente da un doppio strato di fosfolipidi, da una zona centrale ad alto contenuto d'acqua e quindi conduttiva ed infine da un nucleo interno.
Considerando il doppio strato fosfolipidico, che costituisce la membrana cellulare, come una sfera di raggio R, con una capacità Cm, nel momento in cui venisse applicato un campo elettrico esterno E, si verrebbe ad indurre un potenziale di membrana ![]() dove q è l'angolo tra il vettore relativo ad un punto sulla membrana e la direzione del campo E, R è il raggio della cellula e t è la costante di tempo associata al fenomeno di dispersione b .
dove q è l'angolo tra il vettore relativo ad un punto sulla membrana e la direzione del campo E, R è il raggio della cellula e t è la costante di tempo associata al fenomeno di dispersione b .
Massimizzando la Vm(q ) rispetto a q per w =0 si ha Vm=1.5 · E · R, valore che aumenta all'aumentare di R. E' inoltre importante rilevare che il potenziale Vm per frequenze basse assume il valore massimo. Il fatto che la tensione dipende dal raggio R, pone dei problemi in fase sperimentale. Infatti esponendo ad un campo E un gruppo di cellule di dimensioni diverse, si avranno valori diversi di campo, quindi i risultati non saranno uniformi.
Esempio: Se la d.d.p. tra interno ed esterno della membrana e di 40 mV a riposo, dalla ![]() , si ha che ai capi della membrana e quindi in uno spessore di 10 nm, il campo interno è nell'ordine dei MV/m, che è un valore molto elevato. Da ciò si deduce che i fosfolipidi sono degli ottimi isolanti.
, si ha che ai capi della membrana e quindi in uno spessore di 10 nm, il campo interno è nell'ordine dei MV/m, che è un valore molto elevato. Da ciò si deduce che i fosfolipidi sono degli ottimi isolanti.
Se cresciamo in frequenza, fino a superare il rilassamento b , l'espressione della Vm(q ) (potenziale di membrana) può essere approssimata come :
![]()
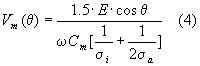
nella quale a differenza della Vm per frequenze minori della frequenza di rilassamento b , intervengono ora anche la s i, s a e la Cm.
Poichè si può schematizzare la membrana citoplasmatica come un condensatore è evidente che all'aumentare della frequenza del campo incidente essa presenterà via via impedenza minore fino a cortocircuitarsi, consentendo al campo interno di raggiungere valori sempre più significativi. Al contrario Vm assumerà valori tendenti a zero.
Esempio: Ad 1 GHz con una densità di corrente extracellulare di 10 A/mē si hanno potenziali dell'ordine dei microvolt.
Uguali considerazioni si applicano per calcolare il campo elettrico nel citoplasma. Il potenziale ai capi della cellula dall'equazione (3) è circa 3RE0. Questa è divisa fra la membrana ed il citoplasma; comunque c'è uno sfasamento di 90° a causa della reattanza capacitiva della membrana. Il campo Ei nel citoplasma è:
![]()
Dalla formula si nota inoltre come al crescere della frequenza potendo trascurare l'uno a denominatore, si ritrovi un campo interno 1.5 volte quello esterno.
Per fare in modo che la trattazione sia più completa ed esauriente, possiamo considerare un modello migliore della cellula considerandola equivalente ad una sfera di raggio R, contenente un nucleo anch'esso sferico di raggio Rn (con Rn << R), con corrispondenti frequenze di rilassamento t 1 e t 2. Supponendo la cellula, schematizzata come in figura, sottoposta ad un campo E ed applicando le formule (3), (4), (5) avremo:
a) potenziale indotto sulla membrana:
![]()
b) intensità del campo nel citoplasma:
![]()
c) potenziale indotto sulla membrana del nucleo:
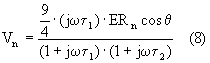
d) intensità del campo nel nucleo:
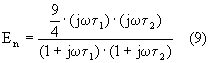
Poiché il rapporto t 1/t 2 è approssimativamente uguale al rapporto tra i raggi cellulari e quelli nucleari, le due frequenze di taglio associate possono differire di un fattore che va da 2 a 10. Le equazioni (6), (7), (8) e (9) evidenziano che al crescere della frequenza, i potenziali sulla membrana cellulare e nucleare tendono ad annullarsi; al contrario nel citoplasma e nel nucleo il campo subisce una amplificazione.
Tutto ciò conferma la validità della teoria svolta con la medellizzazione della cellula semplificata. Inoltre si può osservare come in alta frequenza le coppie di formule (6), (8) e (7), (9) coincidono se la conduttività del citoplasma e del contenuto del nucleo sono uguali.
Se la coincidenza fosse accertata avremmo anche una uguaglianza di impedenze di membrana. Possiamo quindi riaffermare che:
A livello sperimentale c'è un problema non evidenziato nella teoria finora svolta relativo al fatto che quando un gruppo di cellule viene investito da un campo elettromagnetico, se le stesse non sono di dimensioni confrontabili, sperimentano campi di valore diverso rendendo i risultati ottenuti con le (6), (7), (8) e (9) non generali. Globalmente possiamo comunque assumere la trattazione teorica esatta.
E' possibile riassumere i risultati sperimentali della teoria finora fatta in due grafici che rappresentano rispettivamente il campo nel nucleo, nel citoplasma nonché il potenziale all'esterno ed ai capi della membrana cellulare (figura 1).
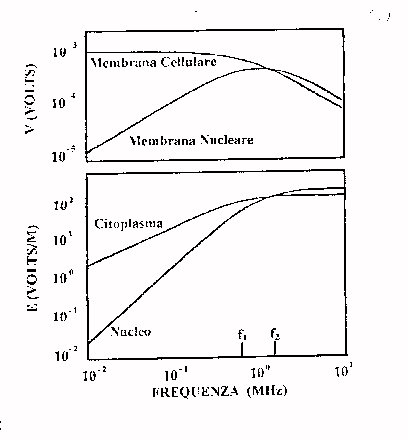
Prendendo come dimensioni standard della cellula R=10-5m e Rm=5·10-6m con frequenze di rilassamento b corrispondenti di 700 kHz e 1.6 MHz si osserva che :
Il campo nel nucleo è trascurabile per basse frequenze (schermaggio della membrana fino alla frequenza f1 della figura 1) così come i potenziali in gioco, anche se si possono sperimentare sulla membrana cellulare che è sottilissima campi elettrici molto elevati. Infatti un campo esterno di 100 V/m crea sulla membrana un potenziale di 10-3 V ed un campo sulla stessa di (10-3V/10-8V)=105V dove 10-8m è lo spessore della membrana.
Si può quindi affermare che è la membrana cellulare la parte della cellula più sensibile alle ELF.
Salendo in frequenza aumenta la caduta di tensione sul citoplasma e quindi sulla membrana nucleare, fino al punto in cui (f=f1 frequenza caratteristica del rilassamento di tipo b ) la membrana cellulare diventa quasi trasparente al campo esterno, provocando sul nucleo la massima tensione (f=f2). Infine anche la membrana nucleare diviene totalmente trasparente. A tal punto il campo interno cresce e riesce a penetrare nel nucleo. Il fatto che le curve relative al nucleo superino, ad alte frequenze, quelle relative alla membrana è dovuto all'amplificazione evidenziata nelle formule.
Nella tabella sottostante sono riassunti i risultati dell'analisi svolta su una cellula ipotetica con un determinato contenuto intracellulare.
|
|
f<f0a (~1MHz) |
f0<f<f0b |
f>f0 (~10MHz) |
|
Cellula Membrana Interno(proteine,ecc.) |
Polarizzato Doppiam.schermato |
Non polarizzato Schermato |
Non polarizzato Esposto |
|
Organelli Membrana Interno(acidi nucleici) |
Non polarizzato Doppiam.schermato |
Non polarizzato Doppiam.schermato |
Non polarizzato Esposto |
|
Organelli connettanti Membrana Interno |
Polarizzato Nonesposto |
Non polarizzato Esposto |
Non polarizzato Esposto |
|
*f0a : Frequenza di dispersione b sulla membrana cellulare |
|||
|
**f0b : Frequenza di dispersione b degli organelli |
|||
Le due maggiori conclusioni che si possono trarre sono:
Le considerazioni suddette suggeriscono che i campi locali nei tessuti risultanti dall'applicazione di campi esterni variano con la frequenza. Questa variazione è anche trovata, in minor grado, in soluzioni omogenee nelle quali i campi locali che agiscono sulle singole molecole sono funzione delle proprietà dielettriche del mezzo e della frequenza. Le membrane cellulari portano a fattori di accoppiamento che presentano una risposta passabanda nei quali il potenziale sviluppato all'interno di una cellula presentano un picco alla frequenza che è intermedia tra la dispersione b della membrana cellulare esterna e quella degli organelli. Questi picchi saranno abbastanza ampi, anche in sospensioni omogenee di cellule e saranno ancora più vasti in tessuti che presentano una grande eterogeneità strutturale.
![]()
Interazione di campi a RF con materia vivente : Risultati sperimentali