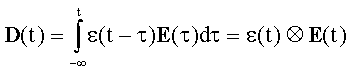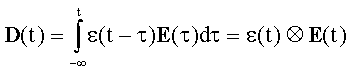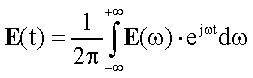Cap4 Equazioni di Maxwell
Espressioni delle equazioni di Maxwell
nel dominio del tempo.
Per la valutazione dei campi si ricorre ovviamente alle:
EQUAZIONI DI MAXWELL NEL TEMPO
m1) Ñ´E(t)=-¶B(t)/¶t
m2) Ñ´H(t)=¶D(t)/¶t
m3) Ñ×B(t)=0
m4) Ñ×D(t)=r(t)
Equazioni dimensionali :
E = [ V/m ] ; H = [ A/m ]
; D = [ Coulomb/m2 ] ;
J = [ A/m2 ]
B = [ Weber/m2 ] = [ Tesla ]
Equazioni costitutive :
D(t) = eE(t) ;
B(t) = mH(t) ;
J(t) = sE(t)
nelle quali sono state introdotte le seguenti grandezze :
e (permittività dielettrica) = [
F/m ]
m (permittività magnetica) = [ H/m ]
s (conducibilità elettrica) = [ S/m
]
r (densità di carica elettrica) = [ Coulomb/m3
]
Dalla prima equazione costitutiva si può considerare anche un
fenomeno di polarizzazione:
D(t) = e0E(t) +
P(t) = e0erE(t)
= eE(t)
dalla quale si ha:
P(t) = e0(er
- 1)E(t) = e0cE(t)
e dualmente:
B(t) = m0H(t) +
M(t) = m0mrH(t)
= mH(t)
Indice del Capitolo 4
Caratteristiche del mezzo
Linearità, omogeneità e isotropia
Caratterizzazione delle grandezze e,
m e s in
base al tipo di mezzo che si considera:
- mezzo non omogeneo Þ
e, m e
s sono funzioni di punto.
- mezzo anisotropo
Þ e, m
e s sono tensori
- mezzo non lineare
Þ e, m
e s sono funzioni di E ed H.
- Se il materiale è non omogeneo, i suoi parametri caratteristici
(e,
m,
s) sono funzioni di punto; ad esempio, nell’uomo, c’è una
disomogeneità tra le caratteristiche della pelle e quelle dei muscoli.
- Se il mezzo è anisotropo, i suoi parametri caratteristici (e,
m,
s) sono dei tensori, cioè sono funzione della direzione (le
ossa possono essere considerate un mezzo anisotropo).
- Se il materiale è non lineare, e,
m e
s sono funzioni di E ed H.
- Se il mezzo è temporalmente dispersivo, c’è un legame causa
effetto tra segnale di ingresso e risposta del sistema(integrale di convoluzione);
ad esempio, un tessuto biologico è polarizzabile fino a certe frequenze
(le molecole d’acqua seguono le variazioni del campo fino a certe frequenze),
quindi i suoi parametri caratteristici (e,
m,
s) saranno funzioni di w e quindi
saranno grandezze complesse (nel dominio della frequenza).
Se, quindi,
il mezzo è temporalmente
dispersivo.
Indice del Capitolo 4
Espressione
delle equazioni di Maxwell nel dominio della frequenza.
Ponendo:
le equazioni di Maxwell diventano:
Ñ´E(w)
= -jwB(w)
Ñ´H(w)
= +jwD(w)
+ J(w)
per mezzi isotropi, lineari, tempo invarianti
e non dispersivi si ha:
D(w)
= eE(w)
; B(w)
= mH(w)
; J(w)
= sE(w)
per mezzi temporalmente dispersivi si
ha:
D(w)
= e(w)E(w)
; B(w)
= m(w)H(w)
; J(w)
= s(w)E(w)
dove e,
m e
s sono grandezze complesse.
Dalle equazioni di Maxwell si nota
che una variazione di campo magnetico crea un campo elettrico e viceversa.
Nell’approccio quasi-statico (basse frequenze, ELF) è possibile
separare campo elettrico e campo magnetico ed ottenere quindi delle semplificazioni
nelle equazioni di Maxwell.
Indice del Capitolo 4
Permittività dielettrica
e e magnetica m.
La relazione di maggiore interesse
è quella tra il vettore spostamento D e il vettore campo
elettrico E; infatti, dalla D(t) = eE(t)
è possibile ricavare la permittività dielettrica e
che è quella che caratterizza il materiale biologico. Si potrebbero
fare le stesse considerazioni per la permittività magnetica m
ma i materiali biologici
hanno una mr
»
1 (permittività magnetica
relativa del mezzo, che è legata alla permittività assoluta
del mezzo dalla relazione: m
= m0
mr
, nella quale m0
è la permittività
magnetica del vuoto); ad esempio l’uomo, dal punto di vista magnetico è
trasparente e quindi la sua presenza non è influente per la misurazione
del campo magnetico prodotto da una sorgente puramente magnetica. Questa
considerazione approssima bene la realtà, anche se, recenti studi
hanno rilevato la presenza di materiale ferromagnetico all’interno dei
tessuti biologici, cioè alcune cellule (1/109) hanno dei piccoli
"magnetini" al loro interno; ad esempio i piccioni, i quali hanno all’interno
della testa del materiale ferromagnetico, riescono ad orientarsi seguendo
il campo magnetico terrestre. Queste considerazioni potrebbero apportare
delle variazioni allo studio dei materiali dal punto di vista biologico
ma, macroscopicamente non si hanno cambiamenti della mr.
La composizione chimica dei tessuti
biologici (costituiti sostanzialmente da acqua e sali) rende il loro comportamento
elettrico ben più complesso di quello magnetico; la presenza di
ioni rende, infatti, il materiale conduttore e c’è inoltre la possibilità
di avere accumuli di cariche all’interfaccia tra due materiali diversi.
Si caratterizzerà quindi
il materiale dal punto di vista dielettrico:
- Se il mezzo non è polarizzabile,
cioè se cambiando il campo il mezzo non cambia le sue caratteristiche,
esso si comporta come il vuoto (e =
e0
cioè er
= 1).
- Se il materiale è polarizzabile
avremo er
> 1; er
è, quindi, una misura di quanto il materiale è
in grado di reagire ad un campo elettromagnetico esterno.
Oltre a trovare i valori della
er per i materiali
in esame sarà interessante capire perché la er
ha un determinato andamento; ci si chiede cioè quali sono i fenomeni
fisici che stanno a monte di questo comportamento.
Lo studio della polarizzazione di
un tessuto biologico può essere condotto sia nel dominio del tempo,
sia nel dominio della frequenza (funzione di trasferimento). In prima approssimazione
è possibile considerare mezzi isotropi, lineari, tempo invarianti.
Indice del Capitolo 4
Homepage tesina 1
Indice generale tesina 1
