In questa tecnica si suddivide il volume di interesse in celle a forma di parallelepipedo :
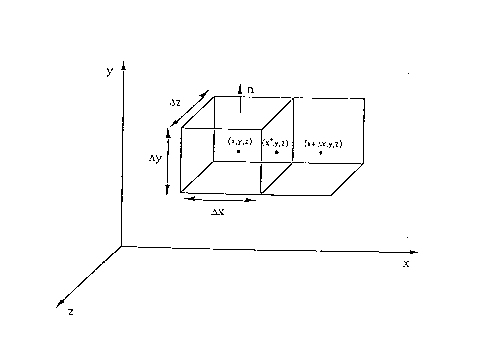
Fig.1
Per valutare la distribuzione del potenziale all' interno
del corpo del soggetto stimolato usiamo una tecnica detta metodo delle
ammettenze o MEAM.
In questa tecnica si suddivide il volume di interesse
in celle a forma di parallelepipedo :

Fig.1
Per ciascuna cella si considera la seconda equazione di Maxwell
( 1 ) ![]()
Nel sistema di riferimento cartesiano considerato , il tensore della conducibilità può essere espresso nella forma
( 2 ) 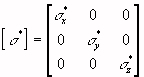
Nell'equazione (1), il campo elettrico (CE), può essere espresso in termini del potenziale scalare (V) e del potenziale vettore complesso (A) come segue
( 3 ) ![]()
Introducendo la (3) nella (1) , integrando sul volume della cella ed applicando il teorema della divergenza otteniamo
( 4 ) ![]()
a questo punto approssimiamo la derivazione in (4) con il corrispondente rapporto incrementale ottenendo
( 5 ) 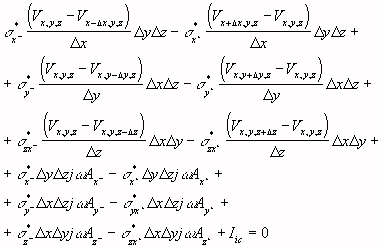
dove Iie rappresenta la corrente impressa
al nodo (x,y,z) positiva quando esce dalla cella. Gli apici + o - nella
espressione indicano che la quantità è valutata su di una
specifica faccia della cella . per esempio s *x+
rappresenta la conducibilità complessa sulla faccia compresa tra
le celle centrate in x e x+D x ( Vedi fig.1). considerando la resistività
complessa r *x+ sulla faccia x+ come la
resistività media fra x e x+ D x noi possiamo introdurre l' ammettenza
( 6 ) 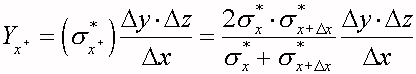
Ammettenze simili possono essere ottenute nelle altre
direzioni. Con questa sostituzione la (5) diviene l' equazione di Kirchoff
per le correnti di un circuito elettrico composto da una stella tridimensionale
di ammettenze e generatori di corrente. La fig.2 mostra il circuito nel
caso bidimensionale .
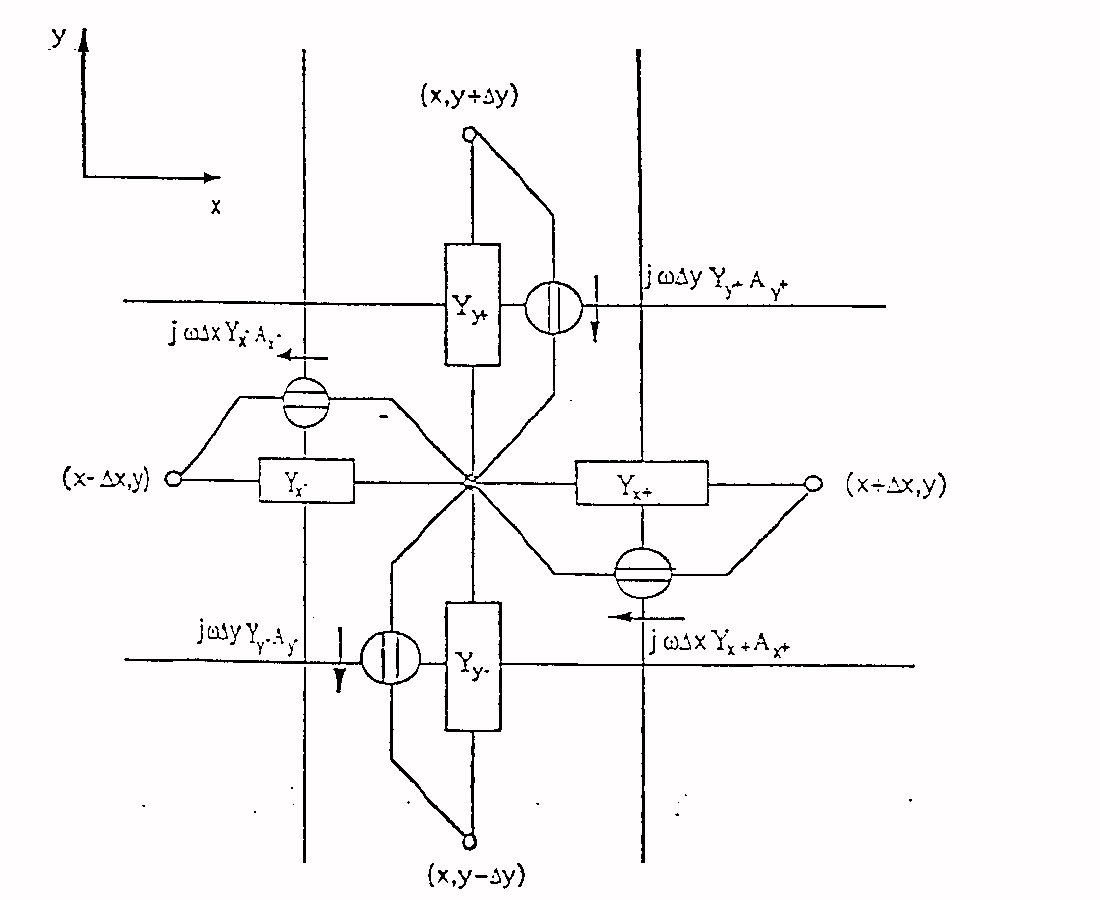
Fig. 2 Rappresentazione bidimensionale del circuito di
base.
Sia per una stimolazione di corrente elettrica applicata
ai nodi direttamente , che per una magnetica applicata attraverso una bobina
esterna , la distribuzione del potenziale nel volume di interesse può
essere valutata risolvendo un sistema di equazioni, una per nodo
( 7 ) 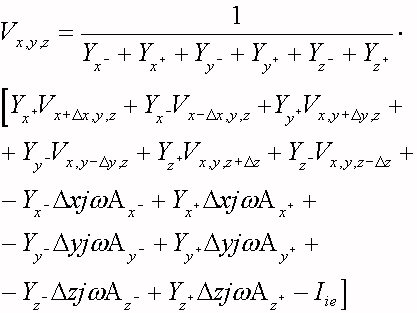
Questo sistema di equazioni è risolto adoperando
un metodo iterativo detto del sovrarilassamento [Ralston & Rabinowitz,1975]
( 8 ) ![]()
![]()
Questa tecnica calcola stime successive del potenziale a partire dalla stima precedente a cui viene sommato un termine correttivo al fine di accelerare la convergenza della soluzione . a è un parametro che può assumere valori compresi fra 1 e 2 ; più elevato è a maggiore sarà la velocità di convergenza anche se per valori prossimi a 2 possono verificarsi fenomeni di oscillazione.
Il procedimento si arresterà quando risulterà verificato il seguente criterio
( 9 ) 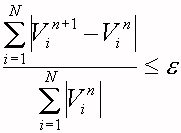
dove N è il numero totale delle celle [Veltink et al., 1989].
Nella stimolazione magnetica occorre preliminarmente
valutare il potenziale vettore sulle facce delle celle a partire dalla
posizione e dalla corrente della bobina. Come riportato in Polk [1990],per
le frequenze , conducibilità e distanze di interesse (1-106
Hz ; 0.013-0.5 S/m ; 1-100 mm), possiamo applicare le ipotesi di quasi
staticità che ci permette di considerare indipendenti dalla
frequenza le conducibilità delle celle, di trascurare il campo magnetico
generato dalle correnti indotte nel tessuto e di esprimere il potenziale
vettore con la formula:
( 10 ) 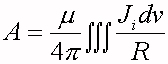
dove Ji rappresenta la densità di corrente volumetrica che fluisce nella bobina e che genera il campo magnetico (CM). Il potenziale vettore nel punto centrale di una faccia di un cella è valutato approssimando la bobina con un poligono a 64 lati e sommando i contributi di ciascun lato [Roth & Basser,1990]. A partire dal valore del potenziale vettore sulle facce è possibile calcolare la intensità di corrente dei generatori (vedi fig. 2). Infine l'equazione ( 7 ) è iterata verso la convergenza.
Supponendo il nervo orientato lungo la direzione dell'asse z le grandezze di maggior interesse saranno la componente lungo z del campo elettrico e la sua derivata spaziale che saranno espresse dalle formule
( 11 ) 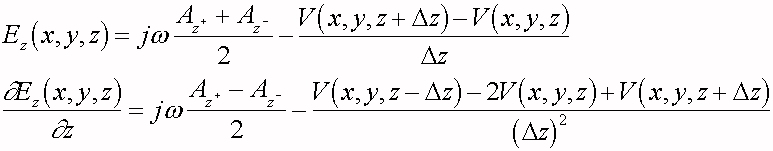
|
|
Il problema principale della stimolazione magnetica è la focalizzazione dello stimolo stesso. Infatti bisogna evitare di stimolare altri nervi o addirittura di iperpolarizzare il nervo desiderato tra il punto di stimolazione e la connessione con il muscolo. Inoltre per una data tensione è importante riuscire ad ottenere la stimolazione massima.
Il problema della focalizzazione è strettamente legato alla forma geometrica della bobina.
Tra le varie forme utilizzate ricordiamo :
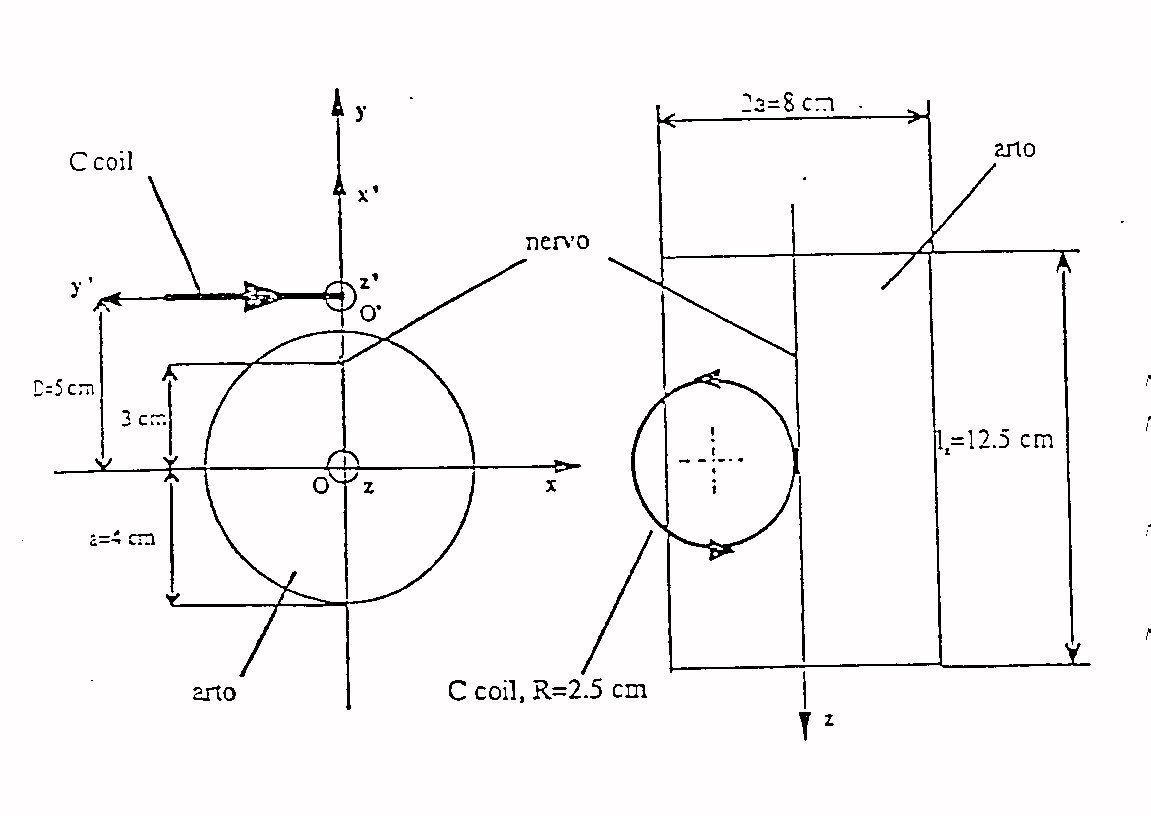
Fig.18 bobina circolare
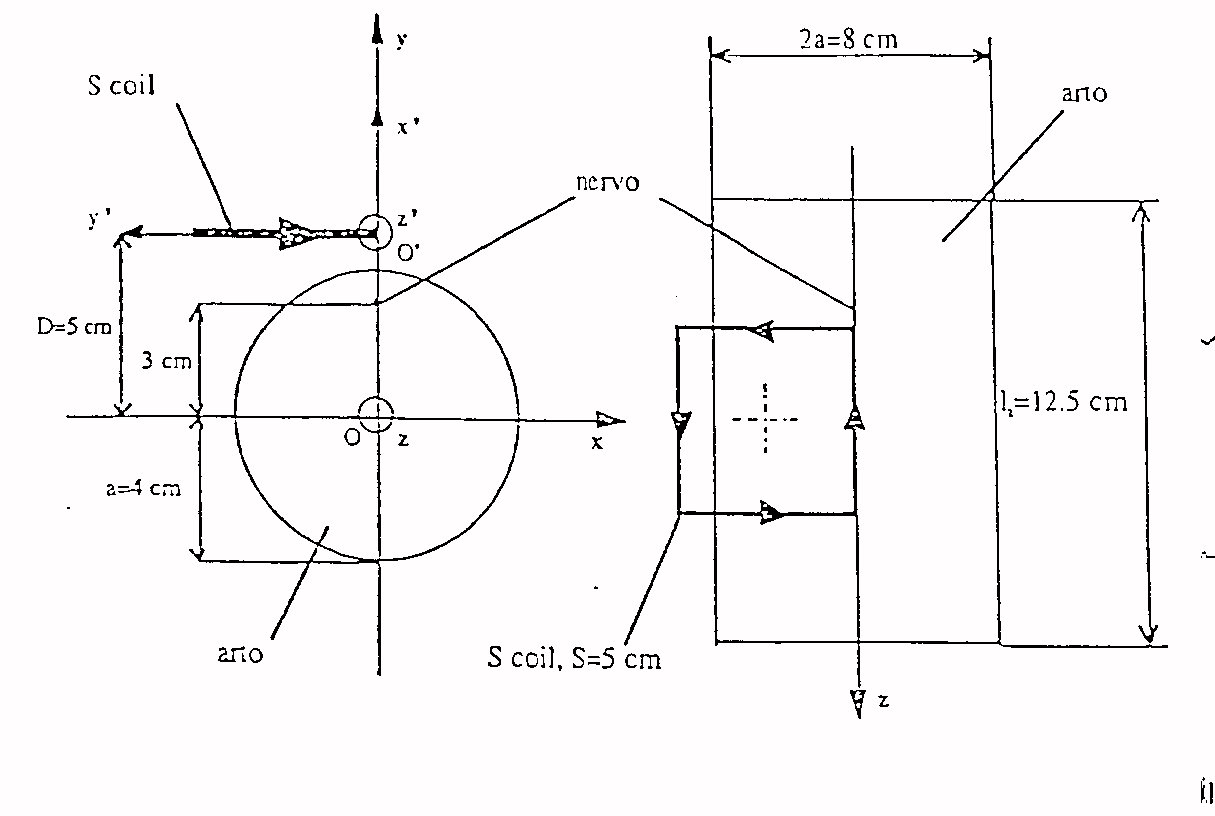
Fig.19 bobina quadrata
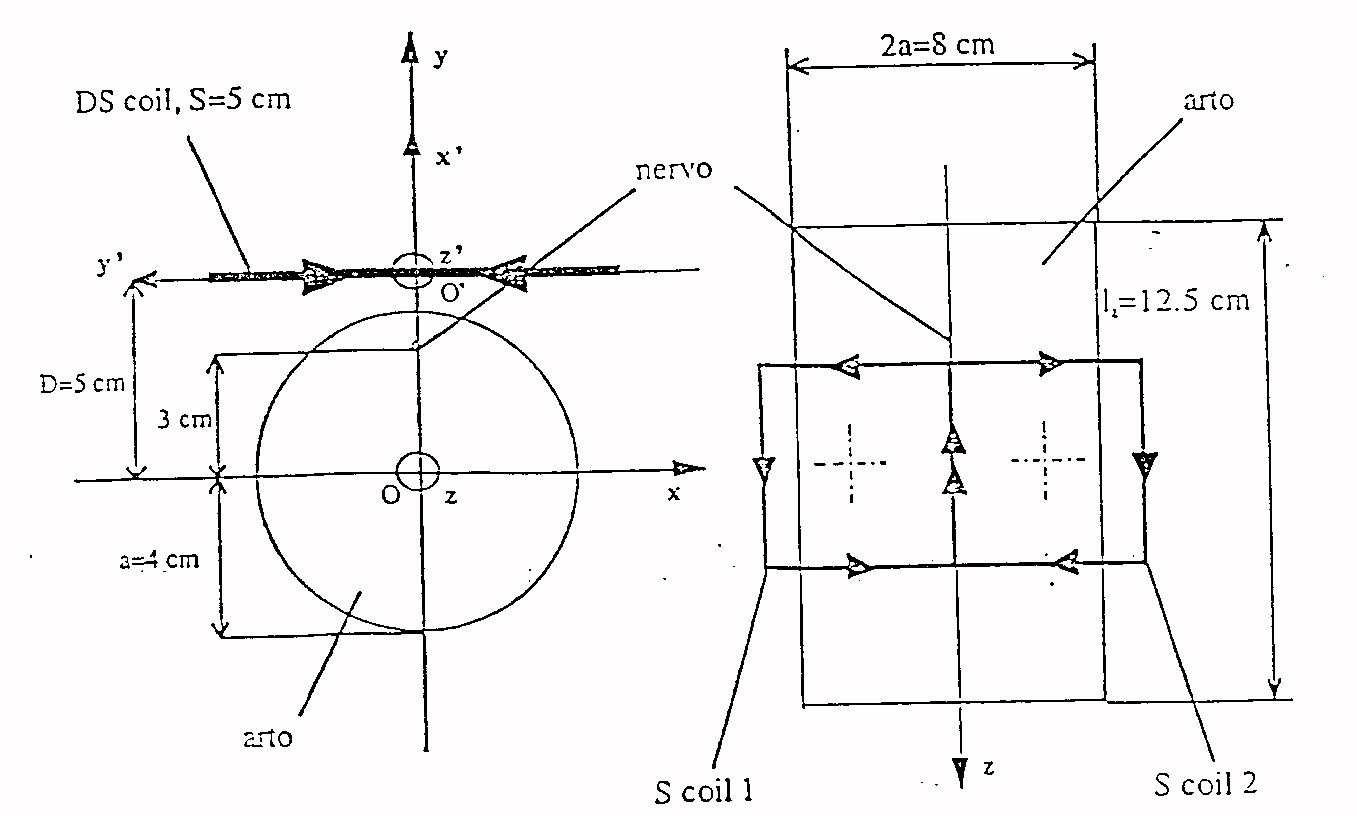
Fig.20 bobina doppio quadrata
Della doppia quadrata esiste anche la versione inclinata
( la cosiddetta " tilded " ) che consente una ulteriore focalizzazione
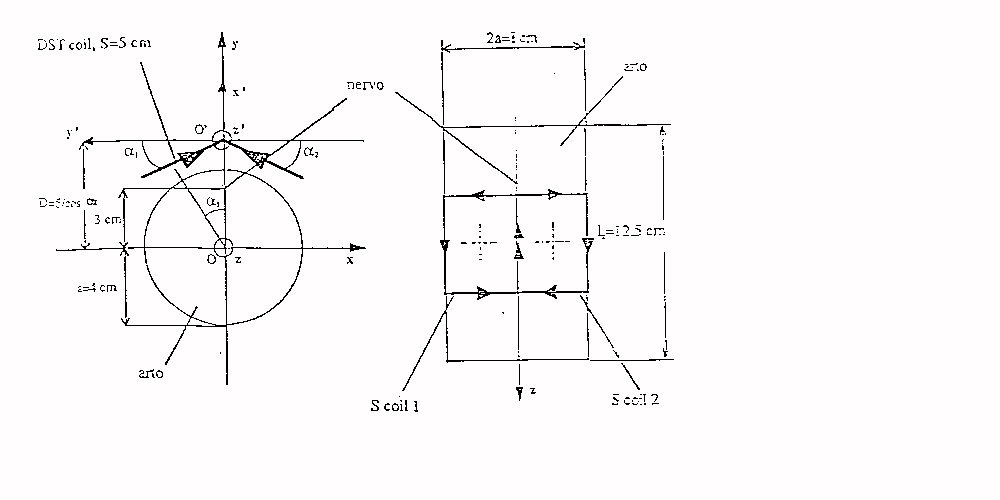
Fig.21 doppia quadrata tilded
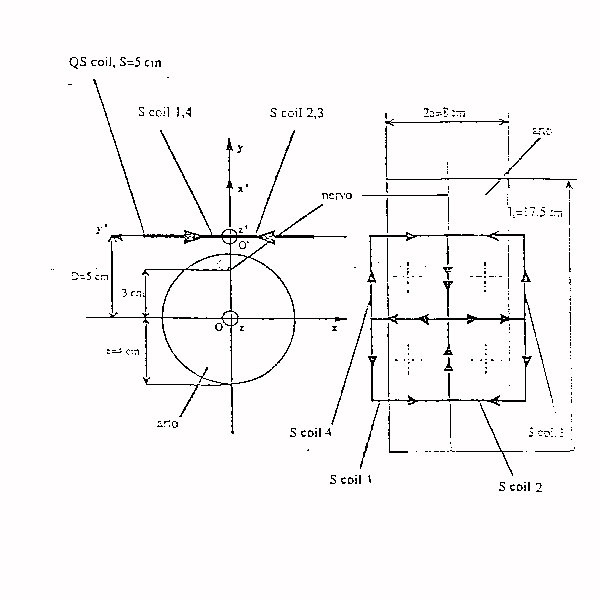
Fig.22 quadrupla quadrata
Un ulteriore versione è la QSTS che consiste in
due doppie quadrate affiancate e inclinate fra loro
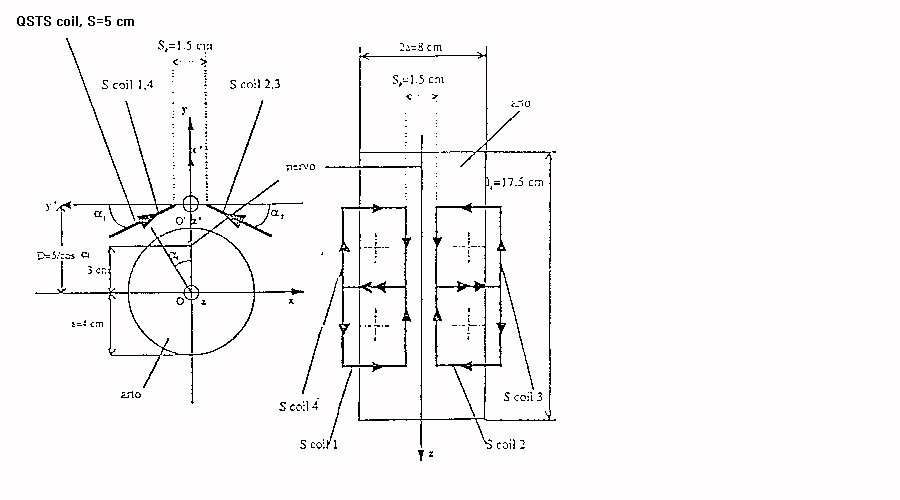
Fig.23 QSTS
Nel caso più semplice della bobina circolare si può esaminare l’andamento della componente Ez del campo lungo la direzione del nervo e quello della funzione di attivazione dEz/dz al variare del raggio .I risultati nel dominio della frequenza sono riportati nelle figure seguenti :
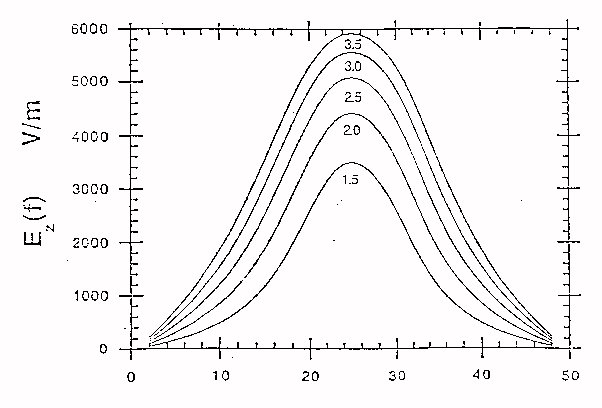
Fig.24
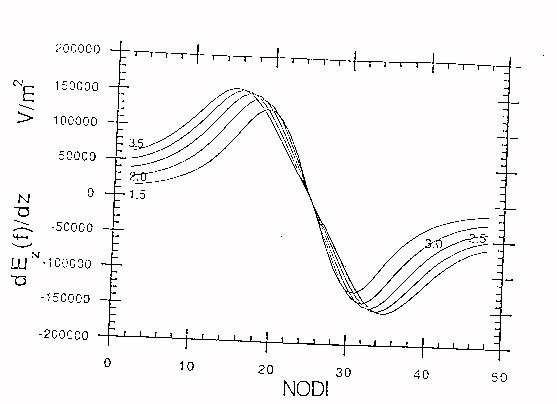
Fig.25
Da tali grafici si può vedere come all’aumentare del raggio aumentino le intensità di entrambe le grandezze considerate ; ciò indurrebbe a scegliere valori elevati per il raggio ma bisogna considerare che oltre ad ovvi problemi di carattere pratico aumentando il raggio aumentano anche l’induttanza e la resistenza della bobina, e quindi per ottenere l’eccitazione del nervo è necessaria una tensione sul condensatore maggiore al crescere del raggio.
Conclusioni
Il metodo sviluppato ci consente di valutare a partire
dalle caratteristiche dello stimolatore la dinamica dell’eccitazione
nervosa nel caso della stimolazione periferica .In particolare riusciamo
a calcolare la distribuzione della funzione di attivazione lungo la fibra,
e quindi a determinare il nodo ove questa funzione è massima.
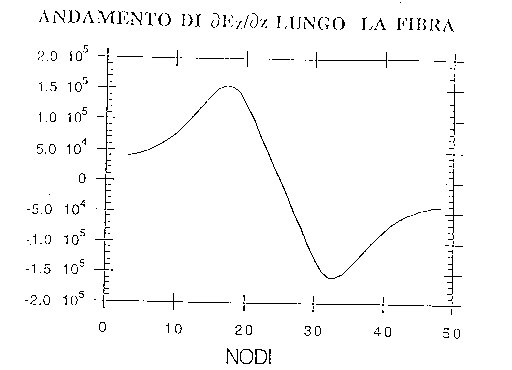
Fig. 26
Per questo nodo è poi possibile determinare l’andamento
della funzione d’attivazione nel dominio del tempo
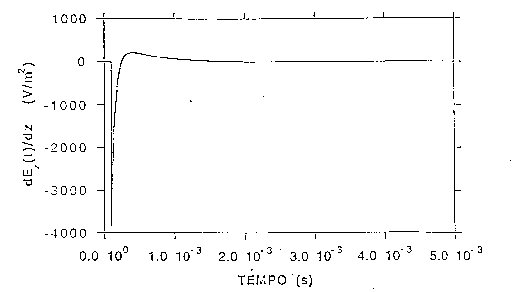
Fig.27
Tale nodo sarà il primo ad attivarsi ; il tempo
di attivazione degli altri nodi sarà poi determinato dalla propagazione
dell’impulso lungo la fibra piuttosto che dallo stimolo esterno ed avrà
l’andamento riportato in figura
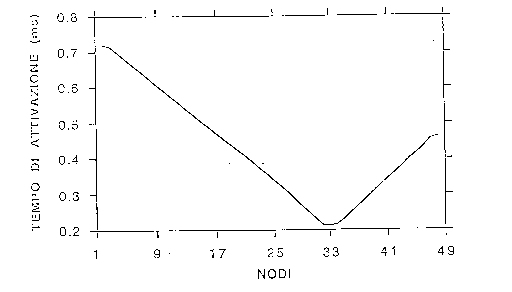
Fig.28.
| INDIETRO | AVANTI |
| TORNA ALL'INDICE |