di
materiale omogeneo (
=
costante, 
=
costante ) tali che al loro interno il campo elettromagnetico sia uniforme.
CAPITOLO 3
DOSIMETRIA SPERIMENTALE
In questo capitolo ci proponiamo di spiegare l'iter percorso dai ricercatori per misurare il SAR su fantocci esposti alle radiazioni emesse da un telefono cellulare in diverse condizioni di esposizione.
Si vuole valutare la potenza elettromagnetica dissipata nel tessuto biologico, nei vari punti e globalmente, quando il mezzo è investito da un campo elettromagnetico incidente.
Si considera una massa M di materiale biologico non omogeneo che occupa
un volume totale V suddiviso in N volumetti di
materiale omogeneo (=
costante, =
costante ) tali che al loro interno il campo elettromagnetico sia uniforme.
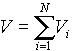(3.1)
Se si chiama 
la
potenza assorbita in 
e
cioè
(3.2)
e si indica la massa contenuta in 
con 
si
definisce SAR la quantità
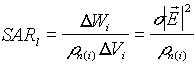[W/Kg]
(3.3)
che fornisce la distribuzione con cui si deposita localmente la potenza elettromagnetica (SAR puntuale, o locale).
Tornando al volume V, si definisce SAR medio il rapporto tra la potenza assorbita nel volume V
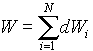(3.4)
e la massa del volume V
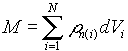(3.5)
sempre misurato in W/Kg. Esso dà un'idea della quantità immessa nell'intero organismo e della sollecitazione alla quale è sottoposto il sistema termoregolatorio.
Dalla linearità delle equazioni del campo elettromagnetico e
dalla proporzionalità tra il SAR e la potenza, se ad una certa densità
di potenza 
nota
si conosce il corrispondente 
,
allora a qualsiasi altra densità di potenza 
nota
il corrispondente 
è
dato dalla seguente relazione
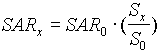(3.6)
Il SAR medio dipende dalla frequenza e dalla polarizzazione del campo elettromagnetico.
L'effetto di focalizzazioni del campo elettromagnetico all'interno di un sistema biologico è dovuto alla rifrazione e riflessione alle interfacce dei diversi tessuti e dipende dalla curvatura del mezzo e dalle proprietà dielettriche dei tessuti stessi.
Una volta definita la grandezza di interesse, il SAR, si passa alla sua valutazione con misure numeriche o sperimentali; ci proponiamo, per ora, di fare un'analisi sperimentale.
Nella dosimetria sperimentale si utilizza un'altra relazione per la misura dei valori di SAR, di più facile applicazione, ottenuta da una forma semplificata ,perché si sono trascurati i termini di 2° grado, dell'equazione di trasferimento del calore; infatti, trascurando i processi di conduzione termica e gli eventuali processi di termoregolazione e limitandosi ad effettuare un'analisi puntuale, si può ottenere la seguente relazione
(3.7)
Essa stabilisce che la potenza assorbita nell'unità di volume è proporzionale all'incremento di temperatura nell'unità di tempo, attraverso una costante k. Poiché k è inversamente proporzionale al calore specifico c ed alla densità di massa r si può scrivere che
(3.8)
Con questa relazione si ha un modo diretto per calcolare il valore di SAR: noto il calore specifico relativo al sistema in esame, conosciamo subito il valore di SAR nel punto considerato se si è in grado di misurare l'incremento di temperatura in un intervallo di tempo limitato. Avendo a disposizione dispositivi termometrici è più facile misurare un incremento di temperatura piuttosto che il campo elettrico interno al tessuto.
Il problema della dosimetria sperimentale è legato alle norme esistenti, nazionali ed internazionali, sui livelli di esposizione a radiazioni RF ed a microonde. In particolare, all'interno di tali norme, le grandezze di riferimento sono il SAR (grandezza base) e le grandezze da esso derivate, quali l'intensità del campo elettrico e del campo magnetico e la densità di potenza esterni al corpo.
Lo scopo delle norme è quello di fissare una soglia per evitare effetti dannosi sul sistema biologico e, quindi, sull'individuo
Le linee guida a cui facciamo riferimento sono
• IRPA/INIRC NRP-GS 11 (1988) [per frequenze da 10 MHz a 300 GHz]
|
|
 (su
6 minuti) mediato su 100 g in corrispondenza delle estremità |
(su
6 minuti) mediato su 100 g in corrispondenza delle altre parti del corpo |
|
| lavoratori | 0.4 W/Kg | 2 W/Kg | 1 W/Kg |
• ANSI/IEEE C95.1 (1992) [standard per frequenze tra 10 KHz e 6 GHz]
|
|
|
(su
6 minuti) mediato su 10 g in corrispondenza delle estremità |
|
| ambienti controllati | 0.4 W/Kg | 8 W/Kg | 20 W/Kg |
| ambienti non controllati | 0.08 W/Kg | 1.6 W/Kg | 4 W/Kg |
• CENELEC (1995) [prestandard europeo per frequenze da 10 KHz a 300
GHz]
|
|
|
(su
6 minuti) mediato su 10 g in corrispondenza delle estremità |
|
| lavoratori | 0.4 W/Kg | 10 W/Kg | 20 W/Kg |
| popolazione | 0.08 W/Kg | 2 W/Kg | 4 W/Kg |
In tali normative non vi è alcun richiamo esplicito ai telefoni cellulari, l'unica cosa che si trova è una regola di esclusione, presente nella normativa ANSI/IEEE, che stabilisce che è possibile, per quei dispositivi che emettono a 900 MHz una potenza di 700 mW, se tenuti ad una distanza di 2.5 cm dal corpo (nel nostro caso dalla testa), eccedere i limiti di massima esposizione forniti.
Se si analizzano i limiti fissati da tali standards si notano forti differenze. Mentre il SAR totale, mediato sull'intero organismo per un tempo di esposizione di 6 minuti, è lo stesso per tutte le normative, il SAR di picco assume valori diversi. Tale discrepanza è dovuta alla diversa scelta di quantità di tessuto su cui si deve mediare.
Nella normativa ANSI/IEEE, ad esempio, si è deciso di mediare su un cubetto di 1 g di tessuto, mentre nel prestandard CENELEC si media su 10 g e nella normativa IRPA si media su 100 g. Ci si deve assicurare, quando si mettono in relazione diversi risultati sperimentali, di considerare gli stessi limiti standard.
Se si confrontano i risultati ottenuti in laboratori diversi ci si deve assicurare che tutti abbiano adottato le stesse procedure di misura in maniera rigorosa. E' necessario, inoltre, fare un'analisi approfondita dell'errore, poiché ogni misura è caratterizzata da un'incertezza che quantifica il discostamento dal valore vero.
I primi studi su fantocci antropomorfi ed omogenei risalgono al 1978.
La difficoltà della dosimetria sperimentale è legata alla rappresentazione delle forme e delle dimensioni di un essere umano, ma soprattutto alla realizzazione di tessuti artificiali con costanti dielettriche pari a quelle dei tessuti reali.
Negli ultimi anni si è scelto di costruire fantocci non più antropomorfi, ma di forma semplice, per problemi legati alla definizione di uno standard nella misura, in modo da realizzare una base comune, per effettuare diversi confronti. Sempre in questa ottica ci si riferisce a modelli sperimentali che realizzino una situazione di "caso peggiore" (worst case); in tal modo si è sicuri di misurare, nel caso reale, un valore di SAR minore di quello trovato sperimentalmente.
Analizziamo, in particolare, il sistema espositivo costruito nei laboratori dell' E.N.E.A., a Casaccia, presso Roma.
Si considera un fantoccio cubico riempito di materiale che, dal punto di vista dielettrico, simula il cervello. Si fa riferimento ad un dipolo che irradia una certa potenza all'interno del fantoccio ed è alimentato da un alimentatore. Il dipolo è del tipo standard commerciale e, quindi, è perfettamente noto il suo diagramma di irradiazione. L'accoppiatore differenziale misura, con un apposito misuratore, la potenza che si sta fornendo alla sorgente. Il sensore viene mosso da un sistema di scansione rappresentato da una struttura mobile in grado di posizionare la sonda in maniera del tutto automatica, in qualsiasi punto del fantoccio.
figura 3.1 - strumentazione del banco di misura
La tensione in uscita dal sensore si misura con un voltmetro; un computer gestisce il posizionamento e l'acquisizione dei dati.
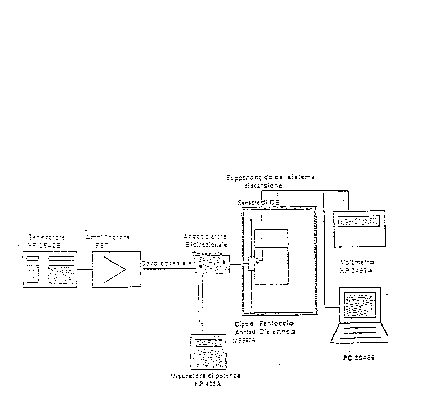
figura 3.2 - schema a blocchi del banco di misura
La situazione reale viene simulata con l'esposizione al telefono cellulare, come si vede nella figura 3.3 .
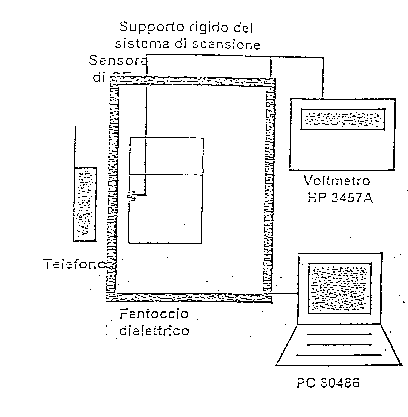
figura 3.3 - schema a blocchi del banco di misura
Il telefono portatile, messo a disposizione da TELECOM ITALIA S.p.A., si trova a lavorare in modalità TEST, cioè è in grado di emettere una potenza costante pari a 0.6 W.
Andiamo ad esaminare i singoli componenti del sistema espositivo preso in esame.
3.2.2 Fantocci dielettrici
I fantocci realizzati nel laboratorio dell' E.N.E.A. sono di forma cilindrica e cubica ed hanno le dimensioni ripotate nella figura 3.4. Il materiale che li riempie è del tipo cervello-equivalente a 900 MHz, costruito con la ricetta, riportata in tabella 3.4, in cui sono evidenti le percentuali in peso dei singoli componenti il fantoccio,fornita nel 1987 da Hartsgrove.ricetta, visibile nella tabella 3.4, in cui sono evidenti le percentuali in peso dei singoli componenti il fantoccio, fornita nel 1987 da
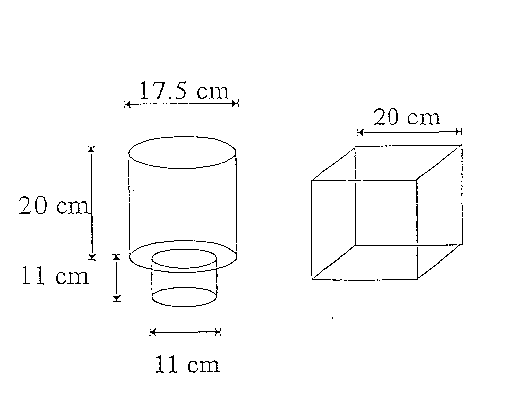
figura 3.4 - fantocci dielettrici
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| e' | s [S/m] | c [cal/g °C] | |
| valori dati da Hartsgrove | 41.2 | 1.22 | |
| valori misurati | 36.73 +/- 1.20 | 0.98 +/- 0.024 | 0.6 |
Si sono verificate due importanti proprietà:
a) partendo dalla realizzazione di un fantoccio con le percentuali in peso defigura i vari componenti forniti da Hartsgrove si sono misurate le costanti dielettriche, come evidenziato in figura 3.5.
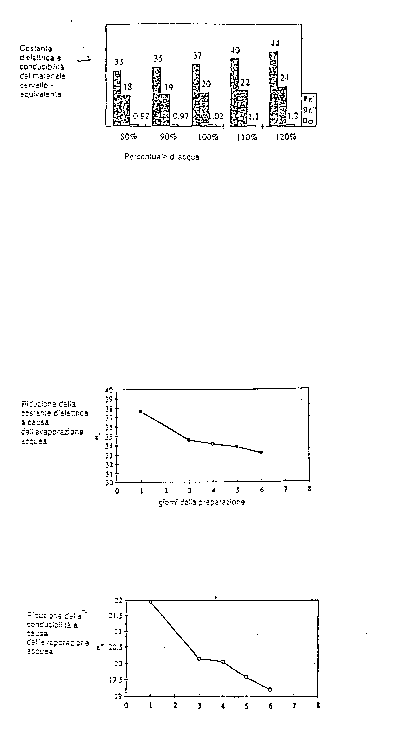
figura 3.5 - proprietà dielettriche del materiale cervello-equivalente
figura 3.6 - riduzione della costante dielettrica con il tempo
figura 3.7 - riduzione della conducibilità con il tempo
Si è notato che aumentando o diminuendo la percentuale di acqua le costanti dielettriche e' ed e" e la conducibilità s variavano in maniera evidente.
b) nei giorni successivi alla preparazione del fantoccio, circa una settimana, si è riscontrata una sensibile diminuzione dei valori di e e s , imputata all'evaporazione dell'acqua.
E' importante, quindi, sottolineare la necessità di ripristinare le stesse condizioni di acqua, ogni volta che si effettua una misura.
3.2.3 Sorgenti
Come abbiamo già modo di dire, le sorgenti usate sono un dipolo commerciale, capace di emettere un campo standard, ed un telefono cellulare che funziona in modalità TEST.
figura 3.8 - sorgenti utilizzate: dipolo commerciale e telefono cellulare
In figura 3.9 viene riportata la schematizzazione del dipolo: esso è costituito da due baffi metallici separati da un gap di una certa dimensione e da un cortocircuito mobile, necessario per l'adattamento del dipolo. La posizione relativa del cortocircuito mobile, così come la dimensione dei baffi, dipende dalla frequenza di lavoro.
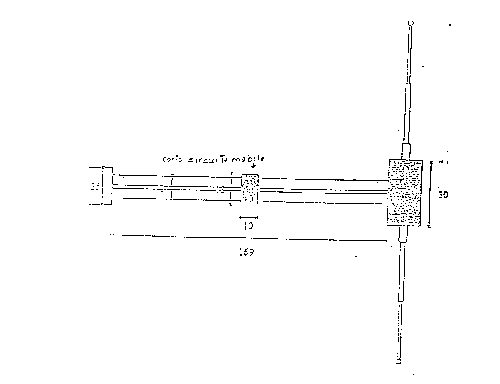
figura 3.9 - schematizzazione del dipolo (le misure sono in mm)
3.2.4 Il sensore
Il sensore è costituito, di solito, da un dipolo di dimensione 0.5 cm. Si utilizza una rete per trasferire il segnale generato ai capi del dipolo ad un detector, elemento atto a rivelare dei segnali. Dopo un filtro passa-basso c'è una linea di trasmissione che fa transitare il segnale in ingresso alla strumentazione di misura.
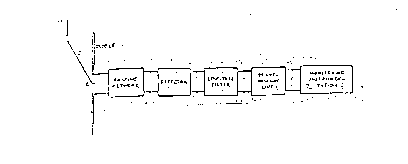
figura 3.10 - schema a blocchi del sistema di acquisizione del segnale
La realizzazione fisica, insieme al circuito elettrico equivalente, del sensore viene rappresentata in figura 3.11.
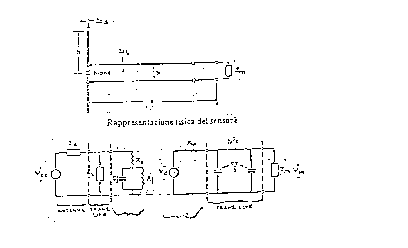
figura 3.11 - (a) rappresentazione fisica del sensore
In corrispondenza del gap del dipolo viene posizionato un diodo Schottky
che rende inutile la rete correttrice, la rete, cioè, che permette
di migliorare le caratteristiche trasmissive della linea, insieme alle
caratteristiche dell'impedenza di linea. Le linee ad alta impedenza trasmettono
il segnale allo strumento di misura, un voltmetro, rappresentato con la
sua impedenza di ingresso, 
.
Secondo le leggi che regolano il funzionamento del dipolo, la tensione che si sviluppa in prossimità del suo gap è proporzionale al valore del campo elettromagnetico presente nel punto in cui si effettua a misura, secondo una costante di proporzionalità, pari alla metà dell'altezza del dipolo, indicata, come si vede in figura 3.11(b), con h.
Il diodo Schottky, a causa della non linearità della sua caratteristica, "vede" ai suoi capi una tensione data dalla somma di una serie di armoniche a frequenze superiori a quella di lavoro, 900 MHz, e di una componente continua; quest'ultima è proporzionale al quadrato della tensione presente al suo ingresso (pari proprio alla tensione del gap del dipolo), quindi proporzionale al quadrato del campo elettromagnetico.
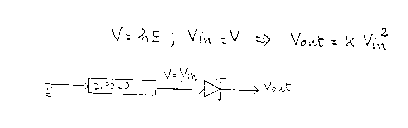
figura 3.12 - funzionamento del diodo Schottky
Il sensore, quindi, invece di leggere il campo elettrico che lo "investe", legge una tensione proporzionale al suo quadrato. La relazione tensione-campo elettrico è la seguente
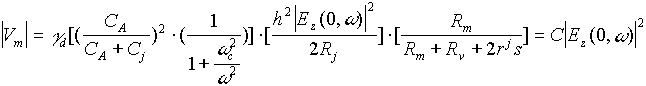(3.9)
Il primo fattore rappresenta il partitore della tensione, cioè la tensione del dipolo tra la resistenza del diodo e la resistenza dell'antenna. La dipendenza dalla frequenza è dovuta al termine capacitivo del diodo Schottky.
Il secondo fattore indica la potenza che viene dissipata nella resistenza 
del
diodo.
Il terzo fattore, infine, rappresenta il partitore della tensione in continua in uscita dal diodo, tra la resistenza di ingresso allo strumento, quella di uscita del diodo in bassa frequenza e la parte relativa alle linee ad alta impedenza.
La validità della (3.9) è rimarcata dalla conoscenza della calibrazione del sensore, C. La gestione del posizionamento e della acquisizione computerizzata dei dati si effettua automaticamente: a tale scopo si utilizza il pacchetto applicativo LABWIEV TM, in grado di acquisire il dato, già opportunamente elaborato, e presentarlo all'utente sul video del computer, simulando non solo il layout del dispostivo di misura, ma anche la sua completa gestione.
3.3 Procedure di calibrazione del sensore
3.3.1 Calibrazione termica
Spesso nella dosimetria sperimentale si usa la calibrazione termica, che si basa sul legame tra il SAR e l'incremento di temperatura. Spieghiamo, ora, come è stata condotta la calibrazione termica, nel caso in esame.
In figura 3.13 è rappresentato lo schema a blocchi dell'apparecchiatura usata per la calibrazione del sensore: in questo caso, poiché si ha bisogno di una potenza piuttosto elevata, circa 50 W (onde ottenere un immediato riscaldamento ed eliminare l'insorgenza di fenomeni convettivi al momento della misura), si utilizza come radiatore un applicatore da ipertermia. Il sensore viene posizionato all'interno del fantoccio, nelle immediate vicinanze, a circa 0.5 cm, della parete su cui, esternamente, viene posto l'applicatore.
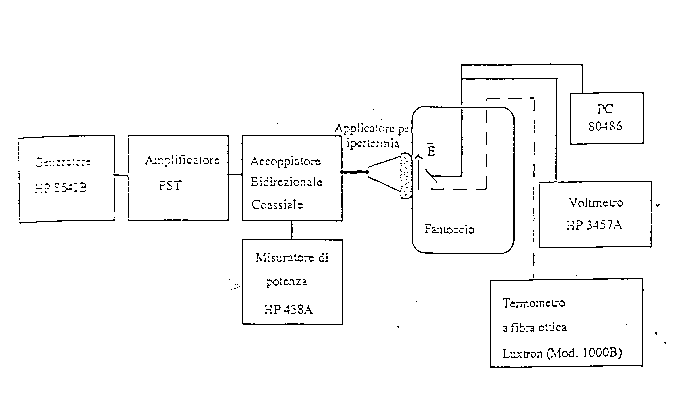
figura 3.13 - schema a blocchi del sistema di calibrazione termica di un sensore
Fornendo differenti valori di potenza e misurando le relative tensioni sul sensore, si realizza la curva rappresentata in figura 3.14.
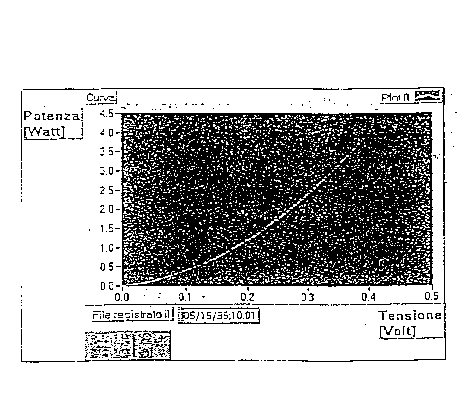
figura 3.14 - andamento della potenza impressa in funzione della tensione letta sul sensore
Nello stesso punto in cui è stato posizionato il sensore si misura, con un sensore di temperatura (da qui il termine termica) la temperatura durante un intervallo temporale di 1 minuto, levando, poi, il segnale.
Poiché il legame tra l'incremento di temperatura ed il SAR è noto ed è dato dalla
(3.10)
si può calcolare il valore del SAR nel punto di misura, se è noto anche il calore specifico c, attraverso la
(3.11)
per potenza incidente di 50 W.
Dalla linearità del legame tra SAR e potenza,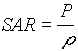 
,
se è noto il valore del SAR a 50 W, si può estrapolare il
valore del SAR a tutte le potenze usate per ottenere la curva di figura
3.14. In questo modo si determina la curva di calibrazione SAR - tensione,
illustrata in figura 3.15.
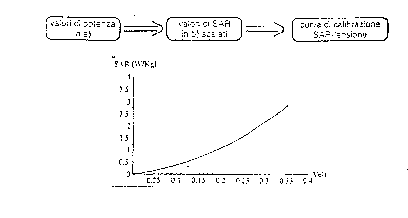
figura 3.15 - curva di calibrazione SAR - tensione
3.3.2 Calibrazione aria - mezzo
Questo tipo di calibrazione utilizza la cella TEM, ossia un tratto di linea in cui può propagarsi un modo Trasverso ElettroMagnetico. Essa è, esternamente, metallica e presenta una sezione rettangolare o quadrata. Poiché per trasportare un modo TEM si ha bisogno di due conduttori, la cella TEM presenta un conduttore centrale, isolato dalle pareti superiori.
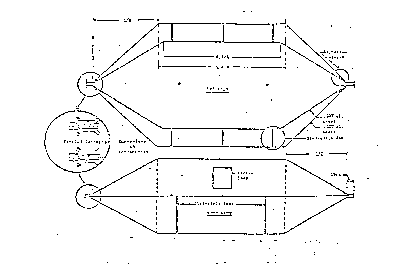
figura 3.16 - cella TEM
Le zone rastremate della cella TEM servono ad adattare l'impedenza del cavo coassiale che la alimenta, 50 W, al corpo della struttura a 3 piatti.
Al centro della cella il campo elettrico è noto ed è dato
dalla relazione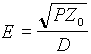 
,
che lega la potenza P con cui si alimenta la cella all'impedenza caratteristica
del cavo coassiale (Z0 circa 50 W),
che alimenta la cella stessa, e la distanza D tra il setto ed il piano
superiore. Il suddetto campo al centro della cella viene utilizzato per
la calibrazione in aria.
Si inserisce, da un'apposita apertura, il sensore nella cella TEM e si misura il campo elettrico; dal confronto tra il valore teorico di campo e quello misurato si ottiene il coefficiente di calibrazione in aria.
Le eventuali deformazioni del campo elettrico nella cella TEM, provocate dall'inserimento di un oggetto, possono essere limitate rispettando alcune relazioni tra le dimensioni dell'oggetto e quelle della cella stessa. In ogni caso, un termine di errore terrà in debito conto queste, seppur piccole, deformazioni.
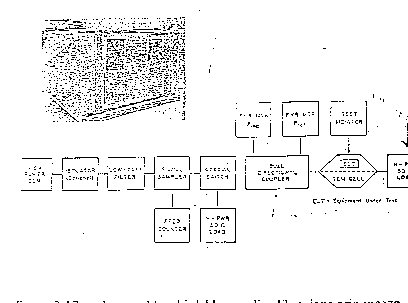
figura 3.17 - schema a blocchi del banco di calibrazione aria-mezzo
Con il sensore sotto esame si misura il campo elettrico all'interno della cella TEM; per determinare il coefficiente di calibrazione in aria, bisogna calcolare il rapporto tra il campo elettrico teorico e quello misurato, cioè
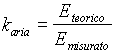(3.12)
Nel mezzo, come è noto, la lunghezza d'onda diminuisce, rispetto
al suo valore in aria, del fattore 
.
In prima approssimazione si fa una scalatura al mezzo utilizzando come
fattore di correzione proprio il fattore di diminuzione della lunghezza
d'onda appena scritto.
Il coefficiente di calibrazione nel mezzo sarà, allora, dato dalla
(3.13)
Poiché si conosce il valore della tensione V misurata in ogni
punto del fantoccio, dalla relazione 
,
precedentemente commentata, si può ricavare il valore del campo
elettrico, utile a determinare il SAR locale, attraverso la ben nota (3.3).
3.3.3 Calibrazione nel mezzo
Questo metodo permette di calibrare direttamente la sonda nel mezzo. Esso prevede l'utilizzo di una guida d'onda rettangolare alimentata, nel caso che descriveremo, a 2.45 GHz. Ovviamente l'esperimento si può ripetere ad ogni valore di frequenza, previo un opportuno dimensionamento del banco di calibrazione.
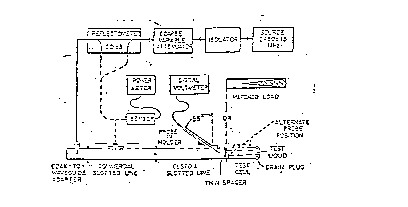
figura 3.18 - schema a blocchi di un banco di calibrazione nel mezzo
Misurando esattamente la potenza che entra nella guida, con un misuratore di potenza, e conoscendo l'impedenza e le dimensioni della guida stessa, si può calcolare, in modo puramente analitico, la distribuzione del campo elettrico all'interno della guida. La guida d'onda viene alimentata da un'estremità ed adattata ad un carico dall'altra; con il sensore posto all'interno della guida si può ottenere il coefficiente di calibrazione in aria. A questo punto si toglie il carico adattato e lo si sostituisce con una cella contenente il mezzo di interesse, nel quale si vuole conoscere il coefficiente di calibrazione del sensore. Tra la cella e la guida sarà presente un setto di separazione.
Si effettuano, ora, due misure ai due lati del setto: la prima misura dal lato dell'aria, la seconda da quello del mezzo. Dalla conservazione della componente tangenziale del campo elettrico tra due mezzi diversi si ottiene che il campo elettrico misurato in aria è uguale a quello misurato nel mezzo. Si possono scrivere, allora, le seguenti relazioni
(3.14)
(3.15)
dove 
,
la tensione del mezzo, e 
,
sono note in quanto misurate e 
è
il fattore di calibrazione già calcolato in precedenza. Si ottiene,
allora,
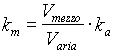(3.16)
La complicazione di questo metodo può consistere nel posizionamento del sensore vicino al setto; infatti, dal punto di vista teorico, le relazioni appena viste valgono solo all'interfaccia tra aria e mezzo.
In realtà, a causa delle dimensioni fisiche del sensore, la misura viene effettuata nelle vicinanze dell'interfaccia.
Si può, quindi, compiere la misura ad una certa distanza dal setto, per poi estrapolare il risultato all'interfaccia facendo tendere la distanza dal setto a zero.
3.4 Confronto tra le procedure di calibrazione
Prima di dare i risultati del confronto tra le tecniche di calibrazione termica ed aria-mezzo, illustriamo due importanti concetti, quello di accuratezza e ripetibilità.
L'accuratezza è il parametro che caratterizza la dispersione dei dati sperimentali intorno al valore vero.
La ripetibilità dà una valutazione sulla possibilità
di ritrovare lo stesso valore della grandezza in esame, a parità
di condizioni sperimentali di partenza.
| Calibrazione termica | Calibrazione termica | Calibrazione aria- mezzo | Calibrazione aria-mezzo | |
| Errore percentuale | Errore in dB | Errore percentuale | Errore in dB | |
| Accuratezza | 19.3 % | 1.53 dB | 25.4 % | 1.96 dB |
| Ripetibilità | 12.5 % | 1.02 dB |
In tabella 3.5 vengono riportati dei valori di accuratezza e ripetibilità su calibrazioni termica ed aria-mezzo: si sono effettuate misure partendo da determinate condizioni iniziali. Dopo alcuni giorni sono state fatte altre misure, ripartendo dalle stesse condizioni iniziali; per la calibrazione termica si è riscontrato un'incertezza percentuale, sulla ripetibilità, del 12.5%.
Passando all'accuratezza, si sono assunte, in prima approssimazione, queste relazioni:
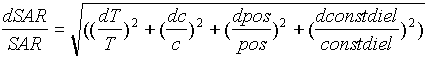(3.17)
e si ottiene 
.
La (3.17) lega la varianza del SAR alle varianze dei singoli termini da cui dipende la misura del SAR; esso dipende: in maniera analitica da calore specifico c e dalla temperatura T, in maniera indiretta dal posizionamento nello spazio del sensore (pos) e dalla misura dei valori di costante dielettrica (constdiel).
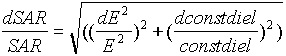(3.18)
da cui si ottiene 
.
Più rigorosamente, la varianza del valore finale di SAR dovrebbe essere legata, mediante opportuni coefficienti di sensibilità, alle varianze dei singoli elementi.
Le misure che sono state effettuate si riferiscono a 3 casi di esposizione:
• a : dipolo accoppiato con cilindro;
• b : dipolo accoppiato con cubo;
• c : telefono cellulare accoppiato con cubo,
come si può vedere dalla figura 3.19 sottostante.
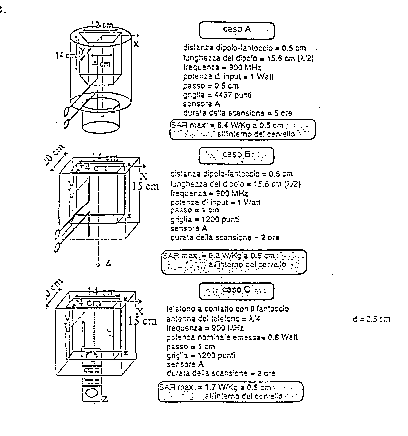
figura 3.19 - misure sperimentali effettuate
Si è calcolata la distribuzione di SAR, ma si è riportata solamente la condizione di SAR massimo.
Le differenze tra i valori di SAR massimo così trovati, e riportati in figura 3.19, sono imputabili alla maggiore potenza di alimentazione del dipolo rispetto a quella del telefono cellulare. In particolare, il SAR massimo riscontrato nel caso del telefono cellulare sembra rientrare nei limiti di sicurezza suggeriti dalle normative.
Nelle figure 3.20 e 3.21 vengono riportati i confronti tra i valori di SAR determinati sperimentalmente e quelli calcolati con il metodo alle differenze finite (FDTD), nel caso c (accoppiamento telefono - cubo).
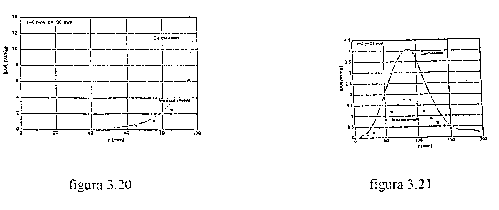
figura 3.20 - figura 3.21
- confronto tra i valori di SAR ottenuti sperimentalmente e da simulazioni numeriche
Si può notare che gli andamenti sono simili, ma c'è una grossa discordanza tra i rispettivi valori assoluti.
Sebbene nella dosimetria, in generale, si siano fatti progressi, ci sono ancora importanti questioni da risolvere:
• il grande disaccordo nei valori limite di esposizione fissati dalle linee guida;
• la mancanza di una definizione rigorosa di misura, tale da costituire uno standard per test di conformità di apprecchi radiomobili;
• la grande variabilità dei risultati ottenuti dai diversi gruppi
di ricerca nella valutazione di casi canonici di esposizione (dipolo+sfera;
dipolo+cubo) ha portato a grandi differenze nei risultati conseguenti all'applicazione
di metodi numerici.
(su 6 minuti)
