• 3.2.1 Modelli di tessuto sferici

3.2.2 Modelli di tessuto sferoidali allungati

Corpi di rivoluzione

Sebbene la profondità di penetrazione ed i dati di riflessione e trasmissione per strutture di tessuto planari forniscano una considerevole interpretazione fisica sull'accoppiamento e la distribuzione di energia delle onde radio e delle microonde, i corpi biologici generalmente hanno una forma più complessa e presentano una notevole curvatura che può modificare la trasmissione e la riflessione dell'energia delle onde suddette. Per corpi con forma complessa, le caratteristiche di propagazione dipendono in modo critico dalla polarizzazione e dalla orientazione dell'onda incidente rispetto al corpo oltre che dal rapporto tra la dimensione del corpo e la lunghezza d'onda. Queste complicazioni pongono severi limiti ai calcoli della riflessione e della trasmissione per corpi di forma arbitraria e permettività complessa. La parte seguente presenta una sintesi dei risultati analitici/numerici che sono stati ottenuti per modelli omogenei e multistrati basati su corpi di rivoluzione che approssimano le strutture di tessuto dei mammiferi.
 

Modelli di tessuto sferici.

La distribuzione entro una sfera dielettrica omogenea del campo elettrico indotto da un'onda piana propagantesi lungo la direzione delle z positive e polarizzata lungo l'asse x è data da

dove a_n^t e b_n^t denotano rispettivamente i modi di oscillazione magnetici ed elettrici entro la sfera ed m_01n ed n_e1n sono due soluzioni indipendenti dette "funzioni vettore d'onda sferica". Esse sono tutte funzioni della lunghezza d'onda, della costante dielettrica, della conducibilità e della dimensione della sfera. La serie infinita dell'eq. 3.5 è facilmente adattabile al calcolo mediante computer usando i valori numerici della permettività dielettrica e della conduttività di interesse. La potenza assorbita è ancora una volta data dall'equazione
 

ed il tasso totale di variazione dell'assorbimento di energia è ottenuto da

 

dove N²=e_r, k₀=2p/l₀, e m₀ e l₀ sono la permettività e la lunghezza d'onda nel vuoto, rispettivamente; j_n ed h_n sono le funzioni di Bessel sferiche ed a è il raggio della sfera.

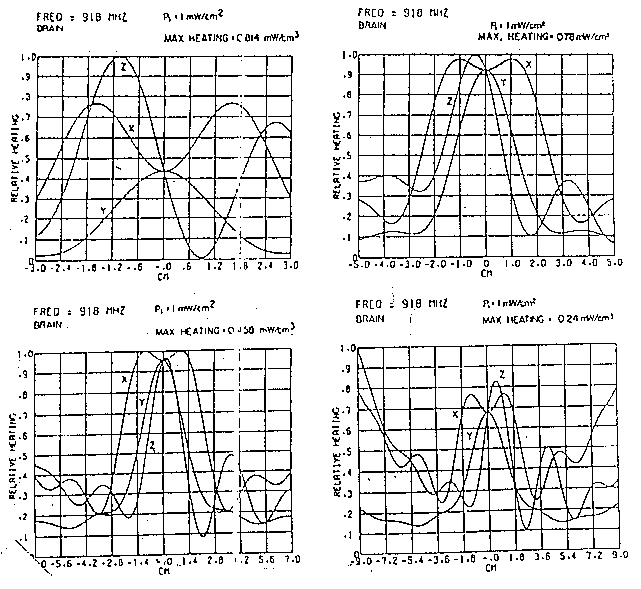
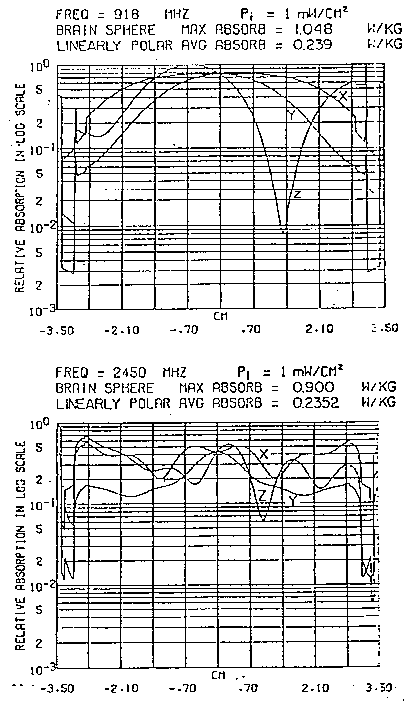
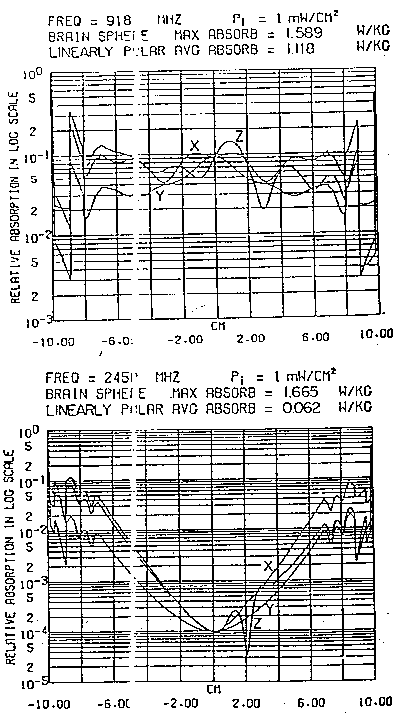
In fig. 3.9 sono mostrati alcuni calcoli rappresentativi del SAR per due modelli a 918 e 2450 MHz (Johnson e Guy, 1972; Lin et al., 1973b). La sfera di 6 cm di diametro approssima le dimensioni del cervello di un gatto o di una scimmia rhesus (Macacus Rhesus: tipo di scimmia antropomorfa) mentre la sfera di 14 cm di diametro è più tipica di un cervello di essere umano adulto. La testa è molto importante per l'alto contenuto d'acqua dei suoi tessuti; in particolare l'occhio ed il cervello. Per essa il modello sferico è un modello accettabile. La fig. 3.9 rappresenta la distribuzione lungo i tre assi coordinati cartesiani l'origine dei quali coincide con il centro della sfera. L'attenuazione è diversa per i tre assi perché è diversa l'orientazione del campo e.m. Siamo sempre in condizioni di campo lontano, cioè abbiamo un'onda piana incidente. E' assunta una densità di potenza dell'onda piana incidente di 10 W/m². 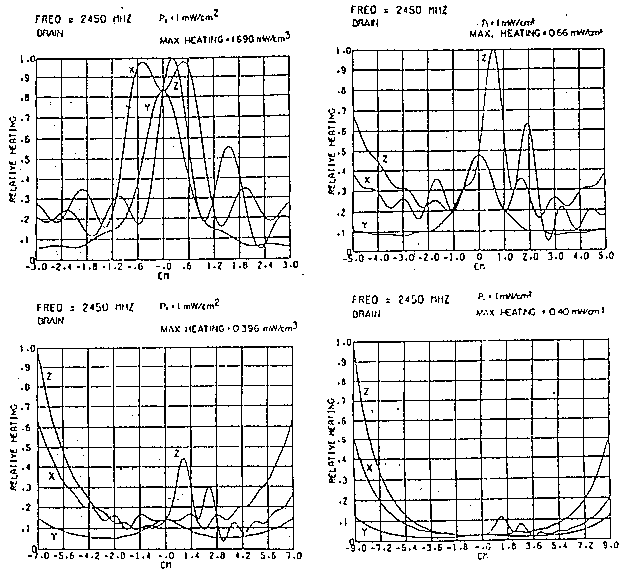Si è visto che a 918 MHz, l'assorbimento massimo si presenta vicino al centro di entrambe le sfere. Quando la frequenza è incrementata a 2450 MHz, la posizione del SAR massimo per la sfera delle dimensioni di un cervello di gatto rimane vicino al centro, mentre per la sfera delle dimensioni di un cervello umano il picco del SAR è ora in una posizione anteriore.
In generale si osservano configurazioni di onde stazionarie con molte oscillazioni. Il valore della frequenza è stato scelto appunto con il criterio che per questi valori si potesse avere risonanza. Si noti che a 918 MHz le curve del SAR nel cervello di gatto sono più larghe di un fattore 2 rispetto a quello umano e che per 2450 MHz l'assorbimento massimo è 4 volte più grande nel cervello di gatto che nel cervello umano. Un confronto tra vari studi disponibili (Shapiro et al., 1971; Kritikos e Schwan, 1972; Lin et al., 1973b; Ho e Guy, 1975) indica che l'assorbimento massimo può essere fino a 5 volte più grande della media e che l'aumento vicino al centro di questi modelli di cervello può essere due o tre ordini di grandezza più grande di quello osservato nei modelli di tessuto planari. Gli aumenti dell'assorbimento sono dovuti ad una combinazione della elevata costante dielettrica e della curvatura del modello, la quale produce una forte focalizzazione di energia verso l'interno della sfera che compensa oltre modo le perdite di trasmissione attraverso il tessuto.
 

Se il diametro più esterno della sfera rimane lo stesso, mentre si ammette che la composizione degli strati di tessuto possa essere sia stratificata che omogenea, i SAR massimi e medi mostrano variazioni molto piccole eccetto quando il raggio della testa sferica è tra 0.1 e 1.0 volte la lunghezza d'onda in aria. I SAR di picco e medi per modelli stratificati possono essere molto più grandi che per i modelli omogenei. L'aumento è apparentemente il risultato di un accoppiamento risonante di energia nella sfera da parte degli strati di tessuto più esterni.

Si potrebbe accennare al fatto che le caratteristiche calcolate dell'assorbimento sono altamente sensibili alla costante dielettrica ed alla conduttività. In letteratura ci sono due tabelle discordanti di costante dielettrica e di conducibilità per il cervello. A seconda dei particolari valori scelti per queste quantità, la valutazione del rischio relativo ai 2450 MHz è variato da un valore minimo a più volte questo valore. La conclusione che 2450 MHz rappresenti una frequenza altamente rischiosa per gli esseri umani deriva più probabilmente dal fatto che nei calcoli è stata usata una costante dielettrica eccessivamente alta (almeno il doppio del suo reale valore) (Lin, 1975; Lin et al., 1975; Schwan e Foster, 1980).
E' stato anche effettuato uno studio sull'interazione di onde piane e.m. polarizzate circolarmente con modelli sferici a sei strati della testa di mammifero (Lin, 1976). L'approccio è di tipo classico; le equazioni di Mie come sono state riportate nelle eqq. 3.5 e 3.9-3.10, vengono modificate per tener conto delle due polarizzazioni che sono ortogonali nello spazio.

Nelle figg. 3.13 e 3.14 sono mostrate due serie di calcoli rappresentativi rispettivamente per 918 e 2450 MHz. La sfera di 7 cm di diametro rappresenta una testa di un gatto o di una scimmia mentre la sfera di 20 cm di diametro è tipica di una testa di un essere umano adulto. In ogni caso, la distribuzione di potenza assorbita è normalizzata al massimo lungo l'asse z. Viene considerata ancora una densità di potenza incidente di 10 W/m².

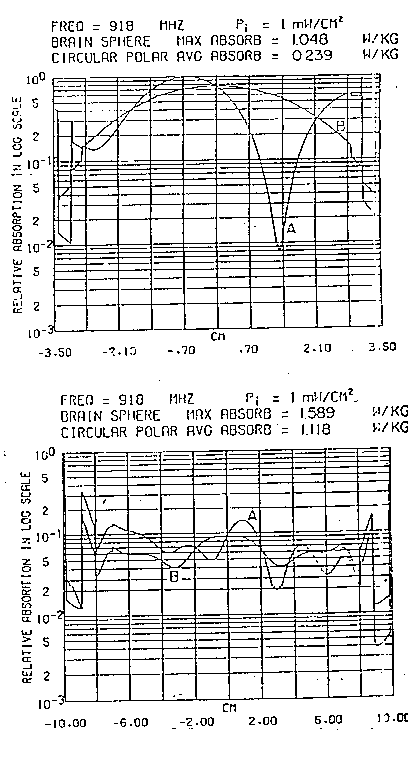
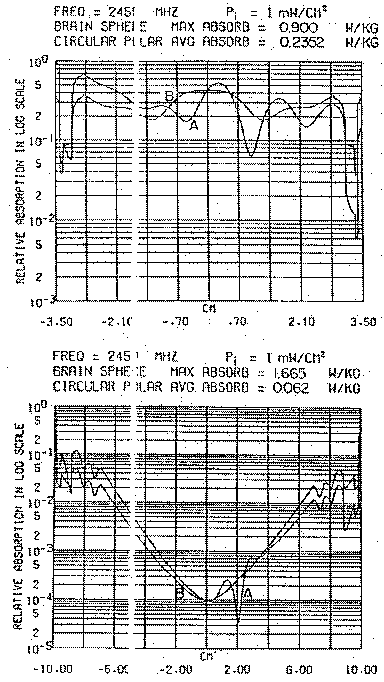
Come per il caso di onde piane polarizzate linearmente, l'assorbimento massimo per 918 MHz si ha vicino al centro per una testa di gatto, mentre per una testa umana è sulla superficie. A 2450 MHz, la posizione dell'assorbimento massimo per entrambe le sfere si sposta alla superficie conduttrice.
La distribuzione dell'energia assorbita per le onde polarizzate circolarmente è risultata più uniforme per il caso di polarizzazione lineare. Infatti, la distribuzione di energia assorbita nei piani ortogonali alla direzione di propagazione è a simmetria cilindrica, cioè essa è indipendente dalla variazione angolare (vedere le curve B). Si noti anche che l'energia massima assorbita nei modelli di testa sferici varia solo leggermente tra le due frequenze studiate. Tuttavia nella sfera più interna (rappresentante il cervello di una testa umana) è rilasciata una maggiore quantità di energia per la radiazione a 918 MHz che per quella a 2450 MHz.
Per alcune ricerche sono state usate sfere di muscolo, come approssimazione del primo ordine, per l'estrapolazione agli esseri umani dei risultati ottenuti da animali di laboratorio  e  come indice  dell'assorbimento  dell'intero corpo dell'energia e.m. in funzione della frequenza. Il modello sferico è interessante poiché possono essere ottenute soluzioni esatte riguardo l'energia assorbita per tutte le frequenze e per tutte le dimensioni del corpo.
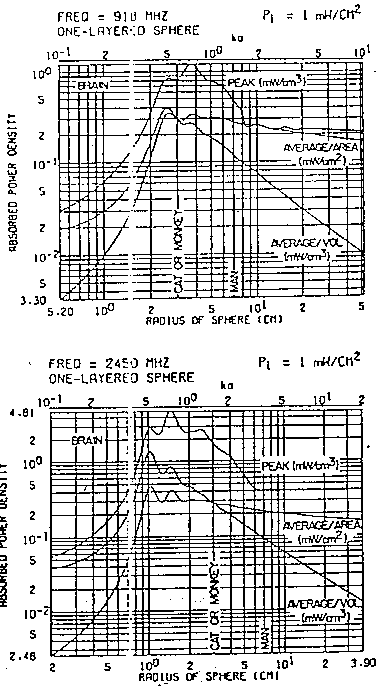
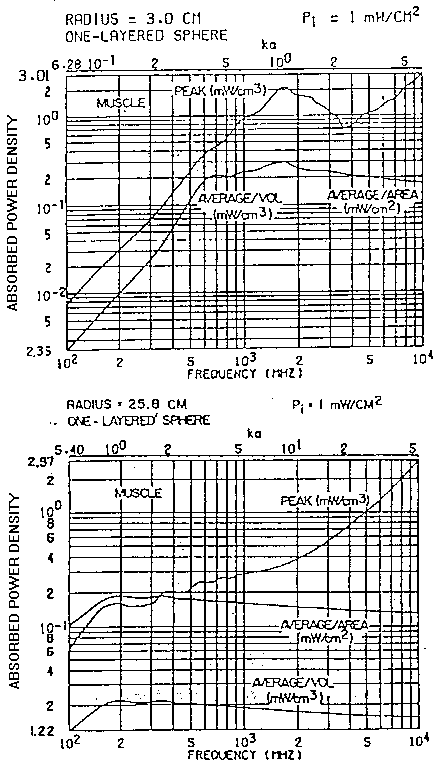
In fig. 3.15 sono riportati gli assorbimenti per le sfere omogenee di muscolo, il cui volume corrisponde a piccoli animali come un ratto oppure ad un uomo standard, calcolati in funzione della frequenza. Mentre in questo caso l'assorbimento massimo non è di grande utilità, l'assorbimento medio per area di superficie unitaria è legato al tempo ed alla potenza richiesta per sovraccaricare la capacità termoregolatrice di un soggetto esposto. Da notare che per frequenze maggiori ai 500 MHz l'assorbimento medio per il modello di ratto è almeno dieci volte più elevato che per una sfera di muscolo rappresentante un corpo umano. Gli assorbimenti in entrambi i casi crescono rapidamente con la frequenza fino a che il diametro della sfera non si avvicina alla lunghezza d'onda nello spazio libero della radiazione incidente.

Un certo numero di oscillazioni risonanti sembra che contribuisca a far crescere la quantità e la non uniformità dell'energia assorbita. Oltre questo intervallo l'assorbimento diminuisce lentamente, indicando che le caratteristiche della curvatura della superficie del corpo sono insignificanti.
Fino ad ora abbiamo affrontato principalmente situazioni ove il diametro della sfera è comparabile o più grande della lunghezza d'onda nell'aria. Quando la sfera è piccola rispetto alla lunghezza d'onda, la distribuzione di energia assorbita varia quasi come il quadrato del raggio o della distanza dall'asse magnetico (l'asse parallelo alla direzione del vettore campo magnetico) come mostrato in fig. 3.16.
 

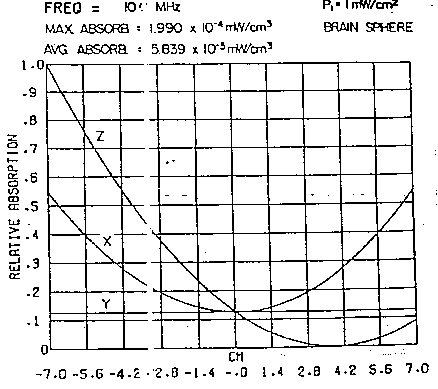
Se la sfera è notevolmente più piccola rispetto alla lunghezza d'onda, la distribuzione di energia assorbita diventa quasi uniforme nelle direzioni x ed y ma decresce continuamente con la distanza dalla superficie esposta (vedi fig. 3.17).

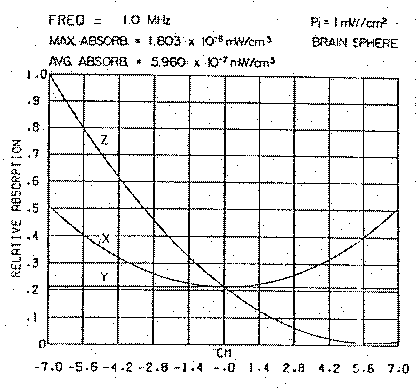
Questo andamento può essere spiegato dalla teoria dei campi quasi statici. Similmente, per un'onda piana polarizzata nella direzione x che si propaga nella direzione z, il campo elettrico indotto entro la sfera dielettrica è dato da:
 
 
 

La componente del campo elettrico dell'onda piana incidente si accoppia all'oggetto nello stesso modo di un campo elettrostatico. Ciò dà luogo ad un campo elettrico costante entro la sfera che ha la stessa direzione ma è ridotto di 3/e rispetto al campo elettrico applicato per i materiali biologici ed è indipendente dalla dimensione della sfera. Similmente, il campo elettrico indotto magneticamente entro il corpo è identico alla soluzione quasi statica la cui ampiezza è data da E=pfmrH, ove f è la frequenza, m è la permeabilità, r è il raggio ed H è la componente del campo magnetico. Così, la componente del campo magnetico dell'onda piana incidente produce un campo elettrico interno che varia direttamente con la distanza dall'asse centrale del corpo e proporzionalmente con la frequenza.
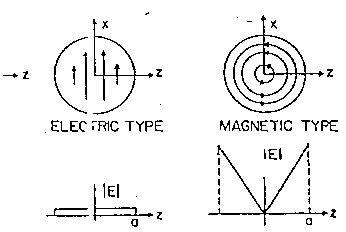
La fig. 3.18 descrive come i campi elettrici indotti si combinano entro la sfera. Il campo elettrico indotto magneticamente circonda l'asse y (asse magnetico) e dà luogo ad una corrente parassita la cui ampiezza cresce con la distanza dall'asse y. Ciò indica che mentre l'assorbimento di energia indotta-H in un topo o un animale più grosso è molto più grande di quello relativo alla componente indotta-E, l'assorbimento indotto elettricamente e magneticamente può essere ugualmente significativo anche in animali più piccoli alle frequenze più basse (sotto i 30 MHz). Inoltre, per un piccolo insetto o crisalide il campo elettrico sarà il fattore dominante.

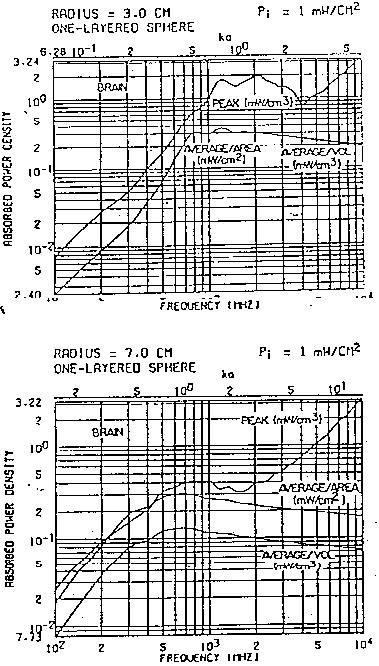
In fig. 3.19 è illustrata la variazione dell'assorbimento medio e massimo dell'energia con la frequenza per una sfera delle dimensioni umane. Nell'intervallo di frequenza tra 1 e 10.000 MHz, la misura dell'assorbimento massimo è solo tra i 10^-6 ed i 10^-3 W/kg per W/m² della potenza incidente. L'analisi della misura dell'assorbimento massimo indotto da un'onda piana, da un campo elettrico quasistatico e da un campo magnetico quasistatico mostra che l'assorbimento nell'intervallo di frequenza da 1 a 20 MHz è principalmente dovuto all'induzione magnetica ed è caratterizzato da una dipendenza dal quadrato della frequenza. La dipendenza approssimata dalla frequenza dell'assorbimento medio o totale dell'energia durante tutto l'intervallo di frequenza tra 1 MHz e 10 GHz è indicata dalla linea tratteggiata.

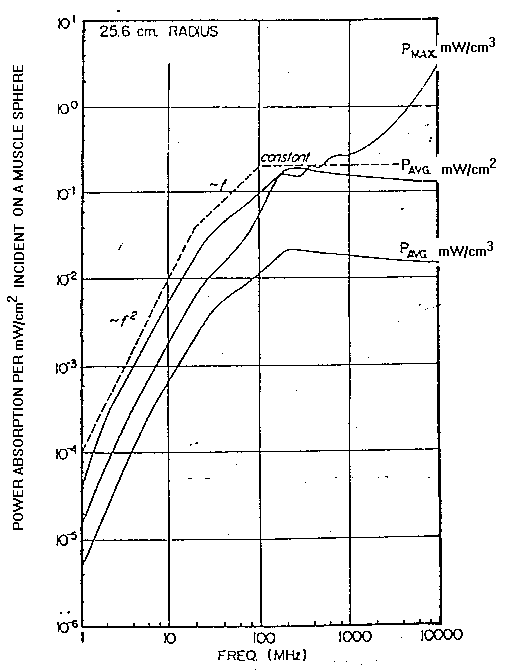
Per le frequenze tra 1 e 20 MHz, l'assorbimento medio varia come il quadrato della frequenza. Nell'intervallo di frequenza 20-200 MHz, l'assorbimento medio è direttamente proporzionale alla frequenza e raggiunge un massimo di circa 2*10^-3 W/kg per W/m² della potenza incidente a 200 MHz. La misura dell'assorbimento medio rimane abbastanza costante con il crescere della frequenza [in realtà è inversamente proporzionale alla frequenza per le frequenze più alte]. Non c'è così alcun dubbio che l'assorbimento dell'energia elettromagnetica vari sia con la frequenza che con la dimensione del corpo, ed in un modo prevedibile.