• 3.2.1 Modelli di tessuto sferici

3.2.2 Modelli di tessuto sferoidali allungati

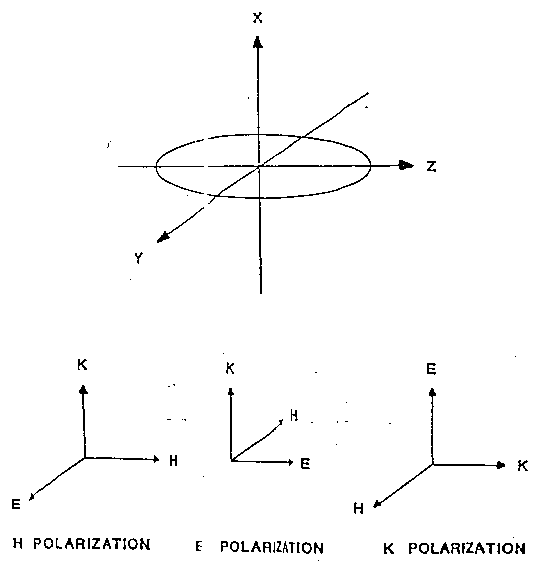
Modelli di tessuto sferoidali allungati.

Poiché i corpi degli esseri umani e degli animali da laboratorio raramente possono essere considerati sferici, abbiamo bisogno di un modello più appropriato per descrivere analiticamente e numericamente i campi indotti e l'energia assorbita. Uno sferoide allungato approssima meglio la forma dei corpi della totalità dei mammiferi, ma la maggior parte degli studi sono stati ristretti ai modelli omogenei per gli esseri umani e per gli animali da laboratorio. L'approccio di base (Asano e Yamamoto, 1975) è quello di espandere i campi elettrici incidenti, scatterati e trasmessi in termini di funzioni d'onda vettoriali in coordinate sferoidali. I coefficienti di espansione sono determinati dalle condizioni al contorno richiedenti che le componenti tangenziali dei campi siano continue attraverso la superficie dello sferoide. La potenza assorbita è ottenuta dall'equazione (P_a =1/2 sE²) e gli assorbimenti medi sono calcolati con relazioni simili alle equazioni viste precedentemente.
Inoltre, alle frequenze inferiori a quella di risonanza (la risonanza è definita come la condizione di massimo assorbimento) per ottenere informazioni sull'assorbimento sono state usate le trattazioni sulle onde lunghe (Durney et al., 1975; Massoudi et al., 1977) e le approssimazioni quasi statiche (Lin, 1980). Più recentemente sono state sviluppate le approssimazioni ottico-geometriche per il calcolo delle caratteristiche di assorbimento nei modelli sferoidali allungati di esseri umani, per le frequenze le cui corrispondenti lunghezze d'onda sono piccole rispetto alla dimensione del corpo (Rowlandson e Barber, 1979).
Anche in questo caso possono essere distinte tre orientazioni dell'onda piana incidente rispetto al corpo (vedi fig. 3.20): la polarizzazione E nella quale il campo elettrico è parallelo all'asse maggiore dello sferoide, la polarizzazione H nella quale il vettore campo magnetico è parallelo all'asse maggiore, e la polarizzazione K nella quale entrambi i vettori campo elettrico e magnetico sono ortogonali all'asse maggiore dello sferoide. In generale, la polarizzazione E produce l'assorbimento di energia più alto per le frequenze superiori o comunque poco al di sopra della regione risonante.

I campi elettrici indotti entro uno sferoide dielettrico allungato (a, semiasse maggiore; b, semiasse minore) investito da un'onda piana e.m. con lunghezza d'onda l>a può essere rappresentato da

per la polarizzazione E e
 

per la polarizzazione H.
La misura dell'assorbimento di energia dell'intero corpo è generalmente data da

dove s=we₀e'' è la conduttività elettrica ed E* indica il complesso coniugato del campo E indotto all'interno del corpo. Le misure dell'energia assorbita dall'intero corpo sono ricavate sostituendo le eqq. 3.13 e 3.14 nella 3.15

per la polarizzazione E e
 

per la polarizzazione H.

Le costanti C₁ e C₂ sono date da

 

Poiché C₁ e C₂ non dipendono da variabili spaziali, i campi indotti entro lo sferoide sono uniformi ed indipendenti dalla dimensione quando il campo esterno è uniforme. Per e'>1, il campo entro lo sferoide è più debole del campo applicato. Inoltre l'assorbimento di energia dell'intero corpo dipende non solo dall'intensità dei campi impressi, ma anche dall'orientazione del campo rispetto all'asse maggiore del corpo.
Come nel caso dei modelli sferici, l'assorbimento è prodotto da una corrente indotta elettricamente nella direzione del vettore campo E applicato, associata ad una corrente circolante indotta dal campo H incidente. E' naturale aspettarsi perciò che l'assorbimento indotto elettricamente sia uniforme, mentre l'assorbimento dovuto alla corrente parassita circolante sia zero al centro e cresca come il quadrato della distanza dal centro.
Le misurazioni dell'energia assorbita in funzione della frequenza e della dimensione del corpo sono state fatte usando materiale muscolare omogeneo sia come indice del SAR nei mammiferi e sia come guida per i dati estrapolati da animali da laboratorio verso gli esseri umani, con particolare riguardo alle medie dell'energia assorbita (Durney et al., 1980).
La fig. 3.21 mostra la dipendenza dalla frequenza calcolata teoricamente dell'energia assorbita per l'uomo e per ratti di laboratorio. Si noti che per una data orientazione del campo incidente il SAR medio per gli esseri umani, dipendendo dalla frequenza, può essere sia più alto che più basso rispetto ai ratti.

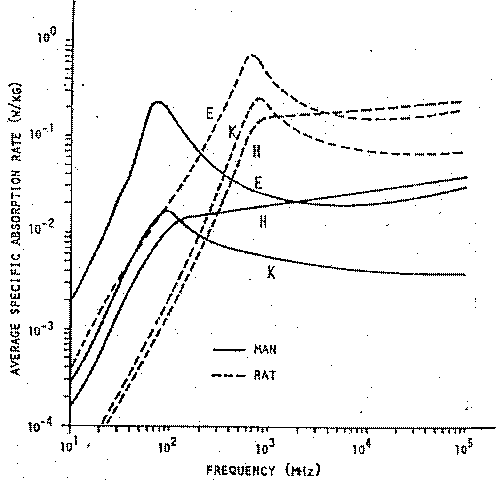
Per esempio, a 70 MHz, il SAR medio è più alto per l'uomo, avendo un valore di 0.25 W/kg per una densità di potenza incidente di 10 W/m²; il SAR medio del ratto è solo 0.0125 W/kg. Al contrario, il SAR medio di 0.8 W/kg a 700 MHz è più alto per i ratti; il corrispondente valore per l'uomo è minore di un 25-esimo. Di questo fatto si deve sempre tener conto quando si ricava una qualsiasi relazione tra gli effetti biologici che sorgono in laboratorio ed i corrispondenti effetti che potrebbero manifestarsi nell'uomo per una data densità di potenza incidente.
La frequenza di assorbimento massimo (frequenza di risonanza) dipende dal soggetto e dalla sua orientazione rispetto al campo incidente. In generale, più basso è il soggetto, più alta è la frequenza di risonanza e viceversa. Inoltre, la dipendenza dalla frequenza dell'intero corpo o l'assorbimento medio può essere suddiviso in tre regioni. Ciò può essere mostrato usando l'orientazione che è più efficace nell'accoppiamento di energia, la polarizzazione E.
La fig. 3.22 fornisce i dati di assorbimento dell'intero corpo per un modello sferoidale allungato di ratto irradiato con onde piane nello spazio libero. Per frequenze ben al di sotto della risonanza tali che il rapporto tra la dimensione maggiore del corpo (L) e la lunghezza d'onda nello spazio libero (l) è minore di 0.2, il SAR medio è caratterizzato da una dipendenza come f². L'assorbimento medio passa per una risonanza nella regione ove 0.2<L/l<1. In questo caso, il SAR medio cresce rapidamente verso un massimo vicino ad L/l=0.4 e quindi diminuisce come 1/f. Alle frequenze per le quali L/l>1.0, l'assorbimento dell'intero corpo decresce leggermente ma approssima asintoticamente il limite dell'ottica geometrica di circa metà della potenza incidente (1 - il coefficiente di riflessione della potenza).

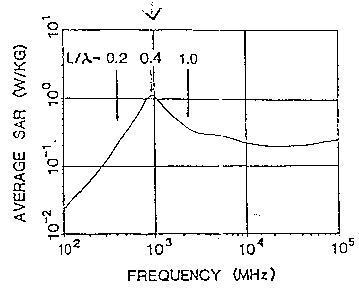
Si potrebbe notare che la lunghezza d'onda di 0.4l dell'assorbimento risonante è in buon accordo con i risultati ottenuti nella teoria delle antenne. D'altro canto, gli assorbimenti dell'intero corpo per le polarizzazioni H e K sono totalmente differenti. Le risonanze non sono così ben definite come per la polarizzazione E. Infatti, la curva di assorbimento dell'intero corpo per la polarizzazione H raggiunge gradualmente un plateau e rimane lì per le frequenze più alte.
La distribuzione dell'energia assorbita in un modello sferoidale allungato le cui dimensioni siano piccole rispetto alla lunghezza d'onda è mostrata in fig. 3.23 per le tre distinte polarizzazioni. L'altezza dello sferoide allungato è di 1.75 m con un rapporto asse maggiore/asse minore di 6.34 e 70 kg di massa corrispondente ad un corpo umano. La costante dielettrica e la conduttività sono quelle per un tessuto muscolare a 10 MHz. Questi grafici sono qualitativamente simili a quelli per i modelli sferici. Come ci si aspettava, l'energia assorbita è più alta per la polarizzazione E. Infatti c'è approssimativamente un ordine di grandezza di differenza nella misura del picco dell'energia assorbita, a seconda della polarizzazione.

 

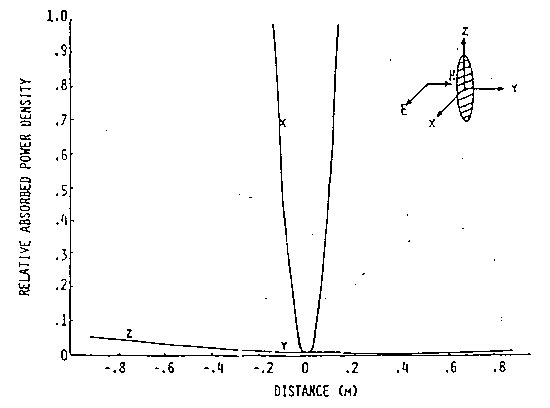
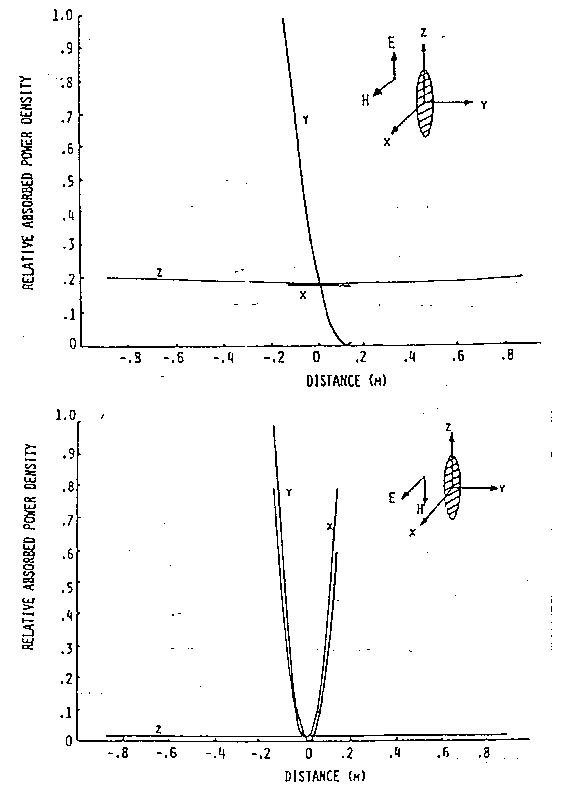
Per la polarizzazione H la corrente indotta elettricamente fluisce lungo l'asse x (direzione del campo E incidente) ed il campo della corrente parassita circonda l'asse z (direzione del campo H incidente). La potenza relativamente bassa sull'asse z proviene unicamente dal campo elettrico incidente. La combinazione delle componenti indotte E ed H genera una configurazione parabolica dell'assorbimento di energia spostata lungo entrambi gli assi x ed y. Chiaramente in questo caso predomina la corrente parassita indotta magneticamente e l'assorbimento è maggiore lungo la circonferenza trasversa passante per il centro dello sferoide allungato.

Per la polarizzazione K entrambe le componenti elettrica e magnetica del campo incidente sono ancora lungo l'asse minore dello sferoide. La corrente indotta elettricamente fluisce lungo l'asse x. Il campo magnetico incidente induce un campo elettrico di corrente parassita che circonda l'asse y e l'assorbimento è più basso sull'asse. Mentre in entrambi i casi di polarizzazione E ed H, l'assorbimento massimo si ha sulla superficie frontale dello sferoide (la superficie dello sferoide incontrata prima dall'onda piana incidente), ciò non avviene nel caso della polarizzazione K. L'assorbimento massimo appare in x=±b e l'energia assorbita varia parabolicamente lungo l'asse x. Ciò deriva dalla grande quantità di flusso magnetico intercettata dalla estesa sezione (e dalla concentrazione risultante della corrente parassita). Si fa notare che i risultati mostrati in fig. 3.23 concordano molto bene con le misurazioni sperimentali. Inoltre gli assorbimenti massimi possono essere anche due ordini di grandezza più elevati di quelli per le sfere dielettriche di uguale massa.

Nelle figg. 3.24 e 3.25 sono riportati gli andamenti della distribuzione di energia assorbita nei modelli sferoidali allungati prossimi alla risonanza per piccoli animali. Per questo caso sono mostrati i quadrati dei campi elettrici indotti; i SAR possono essere facilmente calcolati usando le equazioni viste e le proprietà dielettriche per il muscolo. I grafici in alto mostrano la distribuzione sul piano parallelo al vettore campo elettrico che passa per il centro. I grafici in basso danno la distribuzione sul piano parallelo al vettore campo magnetico che passa per il centro dello sferoide. In tutti i casi è evidente la natura non uniforme della distribuzione: ogni grafico mostra diversi picchi di assorbimento. I campi intensi nei modelli sferoidali allungati sono circa il 30% più alti di quelli previsti usando una sfera. La curva corrispondente per un oggetto sferoidale, normalmente passa poco sopra le curve per le polarizzazioni H e K e ben al di sotto della curva per la polarizzazione E, come d'altronde ci si aspetterebbe da considerazioni sulla simmetria.

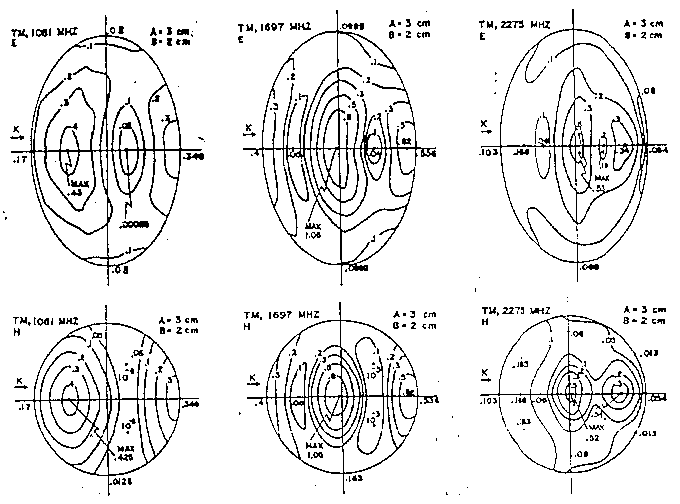
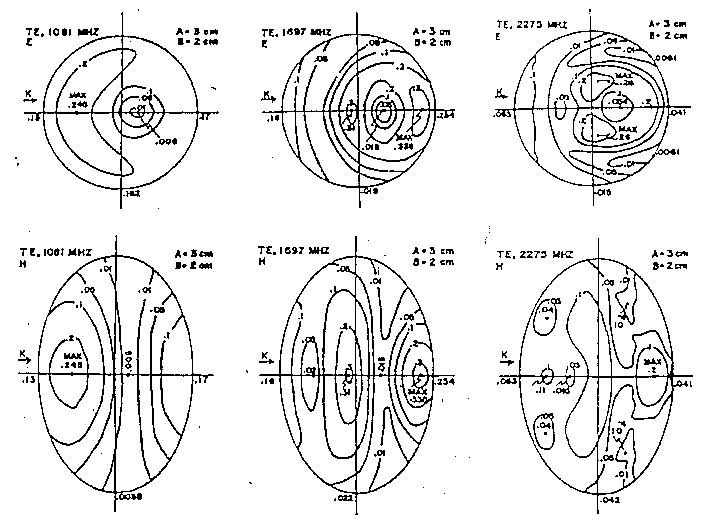
Rimandiamo per ulteriori approfondimenti al testo da cui è stata tratta questa parte:

- S. M. Michaelson & J. C. Lin, "Biological Effects and Health Implications of Radiofrequency Radiation", ed. Plenum Press.