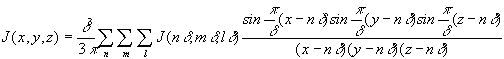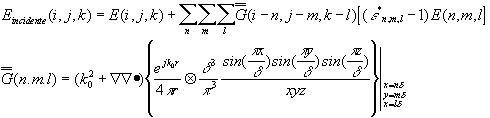METODO
DI MOMENTI (MOM)
E’ un metodo che risale al 1968. Il metodo FDTD
discretizza lo spazio in 4 dimensioni (x,y,z,t) utilizzando
le equazioni di Maxwell.
Il metodo MOM ha un approccio opposto in quanto va ad analizzare
il campo all’interno del mezzo in maniera
integrale, successivamente si discretizza.La procedura di
implementazione di tale metodo è la seguente:
considerando la relazione L(f)=g in
cui :
f è una funzione di tipo integrale o differenziale,
rappresenta la risposta del sistema alle sollecitazioni;
g è il termine noto, in particolare nei problemi
elettromagnetici è l' eccitazione ossia le sorgenti impresse
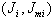 o campi primari.
o campi primari.
L è un operatore.
- Problema di analisi: sono noti g, L incognita f.
- Problema di sintesi: sono noti g, f incognito L.
In generale si cerca una procedura che risolva il problema di
analisi.
L(f)=g
Si opera un espansione in serie di f : 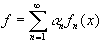
in cui le 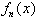 sono
le funzioni base.
sono
le funzioni base.
Approssimando all'ordine N si ottiene: 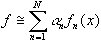
quindi :
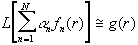
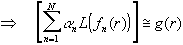
introducendo una serie di funzioni dette funzioni peso 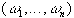 si costruisce un sistema
di N equazioni in N incognite:
si costruisce un sistema
di N equazioni in N incognite:
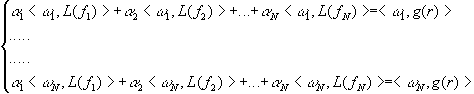
La matrice dei coefficienti del sistema sarà:
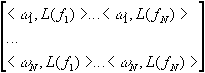
<a,b> rappresenta il prodotto scalare.
Le  devono
essere in grado di soddisfare le condizioni al contorno.
devono
essere in grado di soddisfare le condizioni al contorno.
Per migliorare l'accuratezza si possono scegliere  variabili nel dominio
d'interesse. Un'errata scelta delle
variabili nel dominio
d'interesse. Un'errata scelta delle
funzioni base  può
comportare una cattiva convergenza del procedimento di calcolo
numerico o addirittura
può
comportare una cattiva convergenza del procedimento di calcolo
numerico o addirittura
assenza di convergenza.
Consideriamo che il materiale sia:
- isotropo
- non magnetico
- inomogeneo
Il campo totale in un punto all’interno del materiale è
dato dalla somma del campo calcolato in quel punto, considerando
lo spazio libero (ossia senza materiale) più il campo dovuto al
contributo delle particelle del materiale calcolato come la somma
dei campi generati dalle singole particelle viste come sorgenti
infinitesime equivalenti (è’ un problema di scattering).
Sia:
 il campo
incidente la locazione all’interno del corpo nel punto r
considerando il corpo assente.
il campo
incidente la locazione all’interno del corpo nel punto r
considerando il corpo assente.
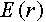 il campo totale
nel punto r.
il campo totale
nel punto r.
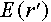 il campo nel
punto r’ all’interno del corpo.
il campo nel
punto r’ all’interno del corpo.
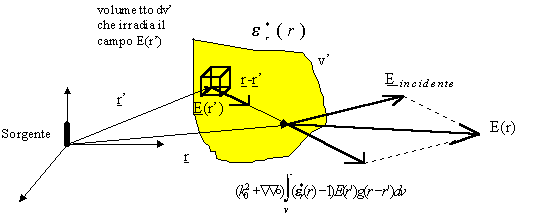
-r variabile corrente
di osservazione del campo
-variabile di posizione
della sorgente
si ha la Electric Field Integral Equation (EFIE):
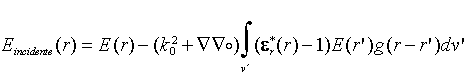
in cui l’integrale corrisponde al seguente prodotto di
convoluzione
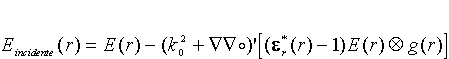
con
 numero
d’onda
numero
d’onda
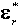 costante
dielettrica complessa alle varie locazioni
costante
dielettrica complessa alle varie locazioni
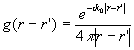 funzione di
Green in tre dimensioni nello spazio libero
funzione di
Green in tre dimensioni nello spazio libero
v’ volume del corpo.
Partendo da tale equazione e scomponendo lo spazio in N
cubetti si otterrà una matrice vettoriale N*N descrivente
l’accoppiamento tra le varie celle. La corrispondente
matrice scalare sarà ovviamente 3N*3N allora l’equazione in
forma matriciale risulta:
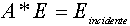
se conosco gli autovalori di A noto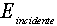 è facile poi trovare
è facile poi trovare 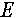
dove:
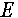 è un vettore
di 3N componenti non noto
è un vettore
di 3N componenti non noto
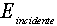 è un vettore
di 3N componenti incidenti le N celle in assenza di corpo.
è un vettore
di 3N componenti incidenti le N celle in assenza di corpo.
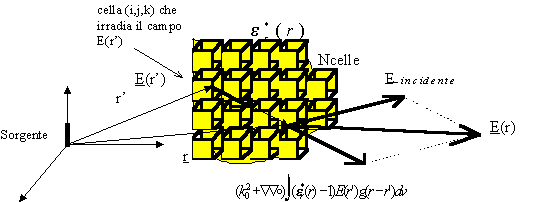
La soluzione dell’equazione matriciale, con il metodo
convenzionale dell’eliminazione di Gauss oppure con il
metodo del gradiente coniugato, richiede un ordine di
moltiplicazioni pari a  e un numero di passi computazionali tra
e un numero di passi computazionali tra  e
e 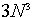 .
.
Questi ordini computazionali crescono rapidamente con
l’aumentare del numero di celle. Di conseguenza non è stato
possibile applicare il metodo tradizionale dei momenti alla
rappresentazione con il modello a blocchi per un numero N più
grande di 1132.
Poiché il prodotto di convoluzione nel dominio delle frequenze
diventa un prodotto sono stati sviluppati algoritmi iterativi
altamente efficienti con la FFT: Fast Fourier Transform.
FFT
La FFT ha permesso di operare su un modello non-omogeneo di
corpo umano costituito da 5607 celle.
Approssimando la sorgente di corrente di polarizzazione  con un espansione
finita si ha:
con un espansione
finita si ha:
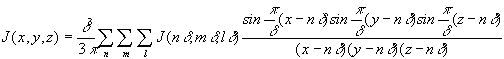
dove d è l'incremento di griglia.
Inserendo tale equazione nella EFIE e forzando l'uguaglianza
di quest'ultima nei punti di griglia si ottiene il sistema di
equazioni :
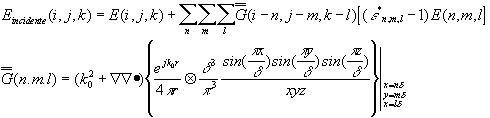
Poiché' la griglia è equispaziata questa equazione può
ereditare la forma di convoluzione dalla EFIE.
Questa forma può essere esplosa in modo tale da ridurre l'ordine
delle operazioni aritmetiche a  ,
,
inoltre, non è necessario memorizzare alcuna matrice dato che
sono richieste solo le componenti 3D di G relative
alle FFT.
Ciò dà un metodo efficiente per calcolare prodrotti matriciali 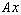 e
e 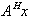 , dove A è la matrice
operatore implicito della equazione precedente (L'apice H indica
la matrice trasposta complessa coniugata), x è un vettore.
, dove A è la matrice
operatore implicito della equazione precedente (L'apice H indica
la matrice trasposta complessa coniugata), x è un vettore.
CGM
Per risolvere il sistema si è usato un metodo di calcolo di
prodotti matrici/vettori di tipo gradiente coniugato(CGM). Il CGM
è diventato recentemente molto diffuso come
mezzo di risoluzione dei sistemi ottenuti con il MOM.
La versione più usata di questo algoritmo fu ideata da Hestenes
e Stiefel e fu introdotta da Sarkar nei problemi
elettromagnetici. Sfortunatamente questo metodo spesso richiede
un grande numero di operazioni per convergere e ciò perché il
CGM si applica solo su matrici ermitiane definite positive.
Applicato a sistemi non ermitiani richiede preliminarmente una
"squadratura" del sistema originale con la matrice
trasposta coniugata, per dare le equazioni normali. Il CGM e'
quindi applicato al sistema ermitiano 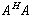 Poiché il numero di iterazioni
necessario per la convergenza è asintoticamente uguale alla
radice quadrata del numero di condizioni, questa procedura può
dare una lenta convergenza. Per superare questa difficoltà il
CGM è stato sostituito con il metodo del gradiente biconiugato
(BCGM) sviluppato da Fletcher, 1975. I1 BCGM si applica
direttamente a matrici non ermitiane senza la formazione di
equazioni normali ed e' stato verificato che converge con
velocità paragonabile al CGM applicato a matrici ermitiane delle
stesse dimensioni. Sono state fatte esperienze con tale metodo
che hanno dimostrato una drastica riduzione del numero di
iterazioni necessarie al CGM applicato a equazioni normali per
sistemi ottenuti dall'equazione EFIE. Dopo aver testato
l'accuratezza della nuova formulazione con sfere di prova,
contenenti materiale dielettrico con perdite, sia interamente
omogeneo, che omogeneo a cubetti, è stato usato un modello di
uomo con 5607 celle esposto ad onde piane a 30 e 100 MHz con e
senza messa a terra. Usando il CRAY II il tempo di calcolo è
all'incirca di 10 minuti. L'occupazione di memoria è
proporzionale al numero N di celle ed il tempo di calcolo è dato
da
Poiché il numero di iterazioni
necessario per la convergenza è asintoticamente uguale alla
radice quadrata del numero di condizioni, questa procedura può
dare una lenta convergenza. Per superare questa difficoltà il
CGM è stato sostituito con il metodo del gradiente biconiugato
(BCGM) sviluppato da Fletcher, 1975. I1 BCGM si applica
direttamente a matrici non ermitiane senza la formazione di
equazioni normali ed e' stato verificato che converge con
velocità paragonabile al CGM applicato a matrici ermitiane delle
stesse dimensioni. Sono state fatte esperienze con tale metodo
che hanno dimostrato una drastica riduzione del numero di
iterazioni necessarie al CGM applicato a equazioni normali per
sistemi ottenuti dall'equazione EFIE. Dopo aver testato
l'accuratezza della nuova formulazione con sfere di prova,
contenenti materiale dielettrico con perdite, sia interamente
omogeneo, che omogeneo a cubetti, è stato usato un modello di
uomo con 5607 celle esposto ad onde piane a 30 e 100 MHz con e
senza messa a terra. Usando il CRAY II il tempo di calcolo è
all'incirca di 10 minuti. L'occupazione di memoria è
proporzionale al numero N di celle ed il tempo di calcolo è dato
da 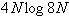 .
.
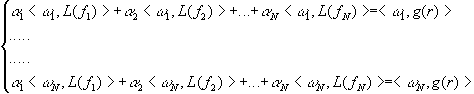
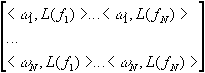

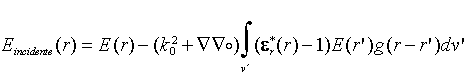
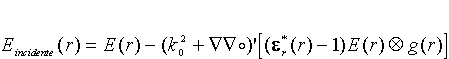
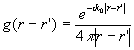 funzione di
Green in tre dimensioni nello spazio libero
funzione di
Green in tre dimensioni nello spazio libero