Per effettuare questa misura si utilizza il modello a linea di trasmissione.

Un primo metodo utile a caratterizzare la costante dielettrica di un campione di tessuto in un ampio range di frequenze consiste nel riempire una guida d’ onda coassiale con il dielettrico in esame; dacché, essendo il modo dominante di tipo TEM, si ha che l’ onda propagantesi nella struttura è pseudo-piana, pertanto  e  sono date dalle:

e 

ove  e sono rispettivamente il fattore di attenuazione e la costante di propagazione dell’ onda nella guida; infatti, essendo l’ onda piana propagantesi lungo l’ asse z della guida descrivibile tramite la:

poiché  si ha:

ove  e ; valendo inoltre per i tessuti biologici la  dalla precedente si può scrivere:

ipotizzando inoltre il tessuto biologico come dielettrico a bassa perdita vale la  da cui , pertanto:

come ulteriore ipotesi si può considerare il tessuto biologico (costituito in buona parte di acqua) buon conduttore nelle frequenze in cui viene effettuata la misura: in tale ipotesi  ovvero

trascurando infine la parte immaginaria (ipotesi di bassa perdita) si ha:

lo schema che si utilizza per la misura di  e  è il seguente:

 

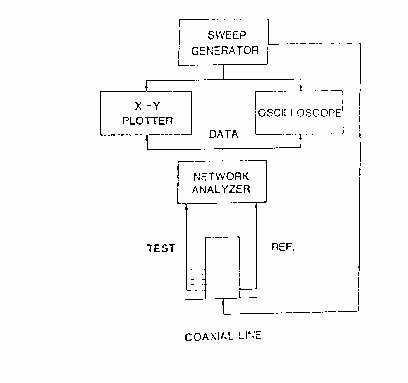
Tramite questa procedura di misura vengono stimati l’ attenuazione ed il fattore di fase. Lo sweep-generator genera un’ onda sinusoidale di frequenza variabile nel tempo, nel campo della radiofrequenza; l’onda viene convogliata nella linea coassiale ed il probe di riferimento (REF) ne rileva la forma che è del tipo . Altri probes vengono posti a distanza z_i (i = 1, 2,..., n) dal REF, in mododa campionare le  (i = 1, 2,..., n) che vengono stimate tramite un voltmetro vettoriale e l’oscilloscopio. Trovandoci in situazione di regime stazionario, i ritardi rappresentati dagli sfasamenti  ci forniscono direttamente una misura dei , pertanto effettuata la stima degli  e  si può diminuire l’ incertezza della stima effettuando una media degli stessi (e. g. media aritmetica: 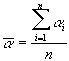 e 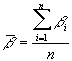). Infine ripetendo gli esperimenti al variare di  (e. g. per  tali che i = 1, 2, ..., s si posssieda uno standard) si possono ottenere le curve  e  interpolando i dati sperimentali con il metodo dei minimi quadrati, che consiste nella risoluzione del sistema

per l = 0, 1, 2, ..., g

con  = incertezze degli standard

e = incertezze della misura

(analogamente procedendo per la curva ). La scelta del grado g del polinomio interpolatore è un problema di ottimizzazione. Infine si vuole sottolineare che per ciò che concerne il,peso delle incertezze (,,) si è riportata una formulazione che prevede un’ incertezza rettangolare: spesso vengono utilizzate ellissi di incertezza.

Più moderne invece sono le tecniche di misura a microonde. In questo caso la guida è riempita di un dielettrico di cui si conoscono le caratteristiche ed il tessuto da misurare, che nel modello a linea di trasmissione rappresenta il carico, chiude la linea tramite opportuni piatti terminali:

 

Un primo tipo di schema è:

 

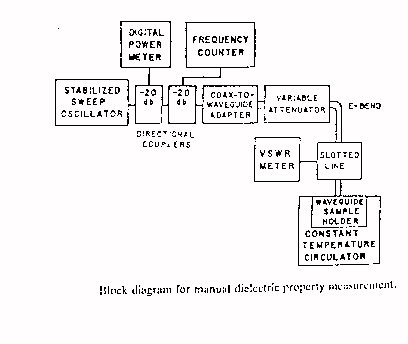
dalla misura del VSWR, della lunghezza d’ onda propagantesi nella struttura  della potenza inviata, delle posizioni ove il campo si annulla con e senza campione (P_a e P_s) e conoscendo la lunghezza d’onda di taglio della guida  si può ottenere  da cui estrarre  e :

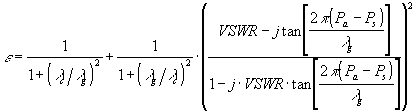
I tempi di misura con questa tecnica sono dell’ ordine dei decimi di secondo, mentre la classe di misura è 2 .

Qualora non sia possibile chiudere la guida tramite un piatto terminale (alloggiamento del campione stesso), la guida viene poggiata direttamente sul tessuto in esame secondo lo schema:

 

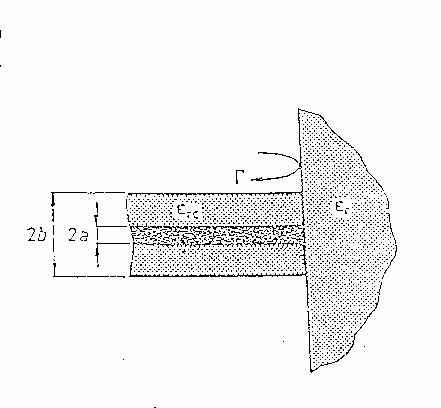
la guida coassiale di diametri 2a e 2b di cui si conosce a priori l’ impedenza caratteristica Z₀, viene chiusa dall’ oggetto della misura che nel caso in questione è un dielettrico di costante . Il circuito equivalente del sistema è pertanto:

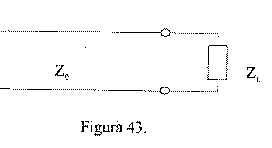
di qui dovrebbe essere immediato risalire ad  dopo la determinazione di Z_L, facilmente estrapolabile misurando il coefficiente di riflessione all’ interfaccia della sonda con il dielettrico. In realtà, non essendo l’oggetto della misura illimitato, una parte del campo si disperderà nel materiale, mentre un’altra si trasmetterà oltre:

 

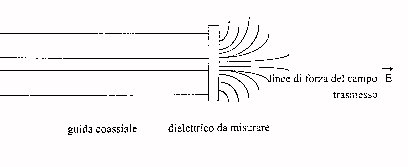
pertanto nella realizzazione della sonda si cerca di realizzare una geometria tale da far contenere all’ interno del dielettrico le linee di forza del campo (figura 45).

 

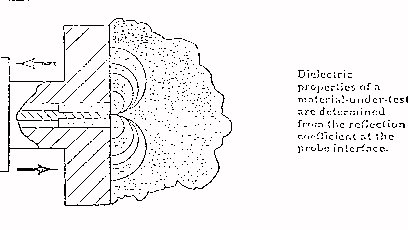
La sonda inoltre - non potendo essere l’aderenza del dielettrico interno alla guida coassiale con quella del dielettrico in esame perfetta - risentirà dell’ incertezza dovuta all’ effetto capacitivo tra il dielettrico da misurare e quello della guida stessa conseguentemente la misura di  perde in accuratezza in misura tanto maggiore quanto più le superfici di contatto non combaciano: tale errore ovviamente si propaga nella procedura di misura secondo la legge di propagazione degli errori; per questo motivo, spesso, nelle specifiche tecniche delle sonde, si trova la raccomandazione che la superficie del dielettrico - qualora esso sia solido - sia piatta e ben levigata:

 

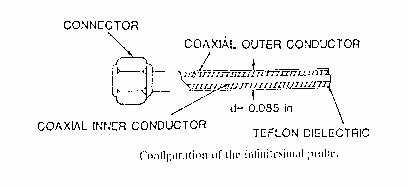
La tecnica sopra menzionata è utilizzata anche per misure in vivo; in tal caso le sonde - placcate d’ oro - sono di dimensioni molto contenute (d2.2mm.), pertanto la misura ha senso nel range di stimolazione .110 GHz:

 

Riferendoci ancora alla figura 42, supposto a, b <<, si può caratterizzare il seguente circuito equivalente:

 

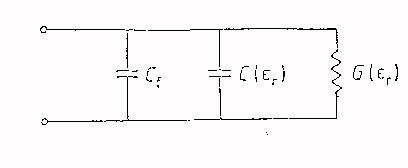
ove C_f è la capacità di bordo del campo interno alla sonda, C() quella dovuta all’ interfaccia con il dielettrico, mentre G() la conduttanza di radiazione; si noti che, oltre alle dipendenze specificate, i tre parametri sono funzione delle dimensioni della guida e nondimeno delle caratteristiche dielettriche del materiale interno alla guida stessa. Per minimizzare l’ errore sistematico si dovrà far sì che il coefficiente di riflessione all’interfaccia sonda-dielettrico_da_misurare abbia dipendenza trascurabile da C_f: operativamente ciò si ottiene facendo sì che C_f sia almeno di un ordine inferiore di C₀. Ciò premesso si invia il segnale al campione e, tramite la misura dei parametri di scattering (l’ analizzatore di spettro fornisce la conduttanza G e la suscettanza B associate al carico che si sta valutando), si risale ai valori di ; in prima approssimazione, trascurando C_f e G₀, si ha che non appena la sonda è posta in prossimità del campione l’ammettenza del carico varia, e la  può calcolarsi tramite la:

Y = G+jB = jC₀(’-j’’) = C₀’’+jC₀’ .

Vista la macchinosità della procedura di misurazione, l’ equipaggiamento di misura è solitamente automatizzato secondo uno schema del tipo:

 

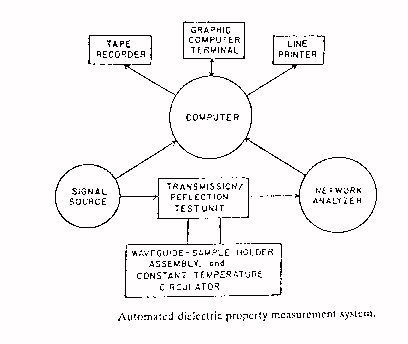
in cui - proprio al fine di standardizzare il processo - la temperatura è fissata (onde tenere conto della dipendenza del materiale dalla stessa) e tutte le geometrie sono predeterminate; in particolare il tessuto da caratterizzare, dopo essere stato accuratamente tagliato, viene incastonato in un contenitore(figura 40); successivamente si estrapolano soltanto i parametri di scattering S₁₁ ed S₁₂ (rispettivamente coefficiente di riflessione all’ interfaccia aria-dielettrico e coefficiente di trasmissione attraverso il materiale dielettrico) da cui:

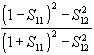Y =  = G+jB

e

 

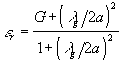
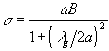
Il campo indotto dalla guida penetra nel campione approssimativamente per una profondità pari al raggio della guida stessa; al fine di farlo penetrare di meno - ovvero per misure superficiali - sono stati realizzati sensori che, tramite opportune lacune aumentano C₀:

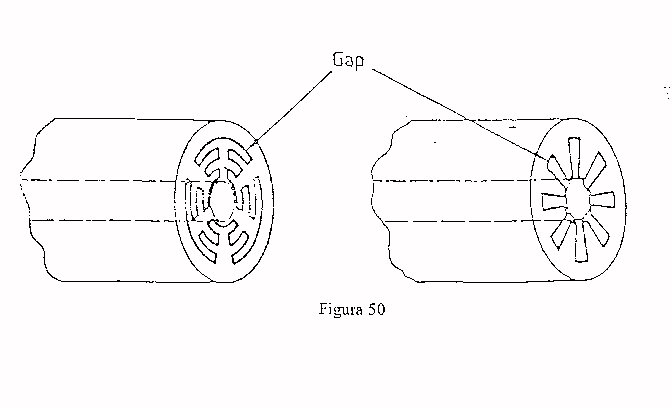
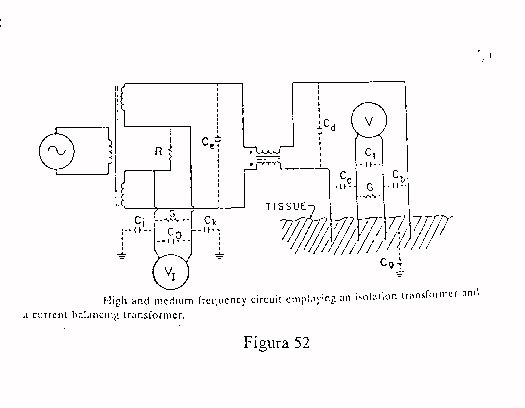
Infine menzioniamo la tecnica standard di misura dei materiali a quattro elettrodi:

 

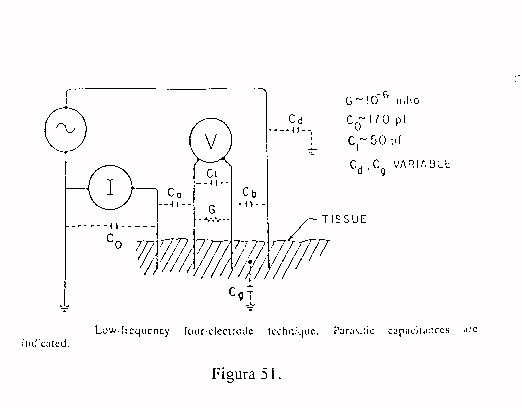
viene fatta scorrere la corrente negli elettrodi esterni e si misura direttamente il campo elettrico tramite il voltmetro; per frequenze medie ed alte il circuito va modificato come segue:

 

 HOME