1.L' acqua
1.3 - Proprieta' elettriche e dielettriche
Lo studio delle proprietà dielettriche dell'acqua e del ghiaccio
è stato a lungo fonte di problemi. Si pensi che verso la fine del
XIX secolo, a Kohlraush ed Heydweiler ci vollero anni per purificare l'acqua
abbastanza da poter stabilire che il limite superiore per la sua resistività
a circa 18 °C aveva il valore di 2,6*105
Wm. Oggi lo stesso risultato si può ottenere in poche ore12,
trovando come limite per la resistività a 25 °C il valore di
1,75*105 Wm, con un'energia d'attivazione
per la conducibilità di 9,7 kcal/mole (0,42 eV di banda proibita
dunque). Stabilire la resistività limite per il ghiaccio è
stato più difficile. E' stato comunque misurato un valore di 109
Wm, ma a causa di effetti di conduzione superficiale si pensa che sia un
valore sottostimato. Considerato che le strutture di acqua e ghiaccio hanno
molte caratteristiche in comune e che la mobilità dei protoni nel
ghiaccio è alcune centinaia di volte maggiore di quella in acqua,
l'alta resistività del ghiaccio sembrerebbe sorprendente, se confrontata
con quella dell'acqua. Ma si pensi che l'energia d'attivazione della conducibilità
per l'acqua pura è pari ad una volta e mezzo l'energia di dissociazione
necessaria per produrre gli ioni mobili H3O+
ed OH-; responsabili della conducibilità
nell'acqua, e quest'energia è dello stesso ordine di grandezza dell'energia
necessaria per rompere quattro legami idrogeno mantenendo la struttura
tetraedrica del ghiaccio già vista in fig. 7. La conducibilità
s può essere calcolata mediante la formula:
s =e( N+
m+ + N+ m
+ )
( 1.5 )
dove N+, N-,
m+, m-
sono le concentrazioni e le mobilità dei cationi e degli anioni.
Sostituendo i valori numerici si ha per l'acqua pura una conducibilità
pari a 6,4*10-6 S/m, in buon accordo con
i dati sperimentali. La differenza di conducibilità elettrica tra
ghiaccio ed acqua può avere implicazioni biologiche. Abbiamo visto
che l'acqua associata con i sistemi biomacromolecolari ha una struttura
tipo ghiaccio se paragonata alla normale acqua, e sembra plausibile che
le proprietà di isolamento elettrico di tale acqua strutturata aiutino
a mantenere gli alti campi elettrici, che sono dell'ordine di 107
Vm-1, e che esistono attraverso le membrane cellulari, riducendo la possibilità
di breakdown. Anche la comprensione delle proprietà dielettriche
dell'acqua e del ghiaccio ha presentato problemi Le caratteristiche di
dispersione e perdita dielettrica per il ghiaccio e l'acqua sono quelle
rappresentate in fig. 12.
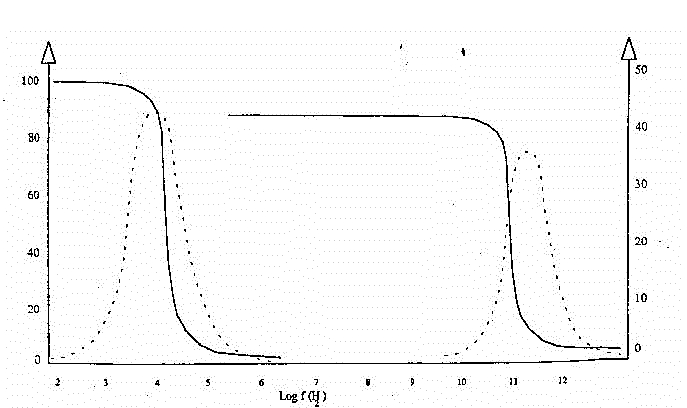Fig.12
L'acqua mostra un semplice spettro di rilassamento alla Debye. L'interpretazione
molecolare del tempo di rilassamento t, fu data,
per primo, da Debye relativamente alle molecole polari. I dipoli ruotano
per l'azione di una torsione T, causata dal campo elettrico applicato,
con una velocità angolare proporzionale alla stessa torsione, secondo
la formula:
T = xdq/dt
( 1.6 )
dove la costante di attrito molecolare x dipende
dalla forma della molecola e dalle interazioni con altri dipoli. Debye
considerò le molecole dipolari come sfere la cui rotazione era ostacolata
dalla viscosità del mezzo circostante. Assumendo allora per la formulazione
di Stokes, cioè:
x= 8pha3
( 1.7 )
dove si è indicato con a il raggio della sfera ed la viscosità
del fluido, Debye calcolò statisticamente tenendo conto delle opposte
influenze dei moti Browniani13
e dell'azione del campo, ottenendo l'espressione:
t = x
/ 2KT = 4pha3 / KT
( 1.8 )
Assumendo per il raggio della sfera un valore opportuno, si ottengono valori
che bene approssimano i risultati sperimentali. Questo è abbastanza
sorprendente, dal momento che il comportamento delle molecole dipolari
di acqua è abbastanza diverso da quello delle sfere in un liquido
non polare, a causa della presenza dei legami idrogeno. Il valore di a
sarà scelto ricordando che l'analisi effettuata è di tipo
statistico14 ed
inoltre, che le molecole d'acqua hanno la capacità di idratarsi,
a causa dei legami idrogeno, nello ione idronio, successivamente, nello
ione H9O4.
E' proprio a tale ione che ci si riferisce per la scelta del valore di
a15. E' da notare
che aumentare la temperatura fa sì che la viscosità del mezzo
diminuisca, con conseguente diminuzione del tempo di rilassamento t,
ossia un aumento cioè della frequenza di taglio del fenomeno; le
molecole sono cioè più libere di muoversi poiché posseggono
una maggiore energia termica, e riescono quindi a seguire più a
lungo il campo. La variazione con la temperatura del tempo di rilassamento
dielettrico indica che l'energia associata all'attivazione dl rilassamento
dipende dalla temperatura, come si può vedere dalla tabella 3.
|
75°C
|
3.7 kcal / mole |
|
25°C
|
4.5 kcal / mole |
|
30°C
|
11 kcal / mole |
Tab.3
Invece, l'energia per attivare il rilassamento dielettrico del ghiaccio,
rimane costante a 13,8 kcal per mole da -80 °C a 0 °C, e probabilmente
corrisponde ad un meccanismo di rilassamento che comporta la rottura di
tre legami idrogeno. Misure sui singoli cristalli di ghiaccio, poi, indicano
la presenza di anisotropia dielettrica. Misure più recenti indicano
poi l'esistenza di sei meccanismi di rilassamento che possono essere visti
dipendere da una polarizzazione intrinseca o da polarizzazioni che implicano
difetti nel cristallo e cariche elettroniche nello spazio. Finora abbiamo
considerato le proprietà dell'acqua pura, che non è un caso
rilevante nei sistemi biologici. La presenza di sali disciolti, poi, e
di altre molecole, modificherà la conducibilità e le proprietà
dielettriche osservate per l'acqua pura. La conducibilità dell'acqua
aumenta fortemente quando vi sono dei sali disciolti in soluzione. Ad esempio,
acqua contenente 0,1 mole/litro di NaCl ha una conducibilità di
1 S/m, un valore di circa cinque ordini di grandezza maggiore che per l'acqua
pura. Per soluzioni di amminoacidi, peptidi e proteine, le permettività
e delle soluzioni diluite sono date dalla:
e = e'
+ 2dc
( 1.9 )
con ' la permettività del solvente puro, c la concentrazione del
soluto e l'incremento dielettrico. Per soluzioni elettrolitiche si è
trovato che la permettività della soluzione è minore di quella
dell'acqua pura, così che d risulta essere
negativo ed è detto "decremento dielettrico". Per queste soluzioni
l'equazione precedente diviene:
e = e'
+ 2d'c
( 1.10 )
con :
d'
= ( d+
+ d- ) / 2
( 1.11 )
I valori dei decrementi elettrici per anioni e cationi di alcuni sali disciolti
in acqua sono tabellati qui di fianco, e valgono per concentrazioni c minori
di una mole per litro. Per stimare, ad esempio, di quanto l'aggiunta di
NaCl riduca la permettività statica dell'acqua, si sommano tra loro
i decrementi relativi a Na+ e Cl-,
ottenendo d = -11.
| Catione |
d+ ( ±1
) |
Anione |
d- ( ±1
) |
|
Na+
|
-8 |
Cl- |
-3 |
| K+ |
-8 |
F- |
-5 |
| Li+ |
-11 |
I- |
-7 |
| H+ |
-17 |
So2- |
-7 |
| Mg2+ |
-24 |
OH- |
-13 |
Tab.4
Quindi la permettività statica relativa per una concentrazione di
NaCl pari a 0,5 moli/litro avrà un valore d'ordine cinque volte
e mezza più basso che per l'acqua pura. Questa riduzione della permettività
è causata dalla sostituzione di molecole polari di acqua con atomi
non polari, combinato con l'effetto di orientamento da parte dell'elevato
campo elettrico intorno agli ioni solvati. I valori dei decrementi dielettrici
dei vari ioni riflettono le differenze dei raggi ionici e del numero di
molecole d'acqua orientate intorno a questi ioni. Questo strato di molecole
orientate non riuscirà a rispondere prontamente all'influenza di
un campo elettrico applicato esternamente e così l'effettiva polarizzabilità
della soluzione risulterà ridotta. La teoria di Debye e Hunkel sosteneva
che per soluzioni diluite, la permettività relativa di una soluzione
elettrolita sarebbe aumenta rispetto a quella del solvente acqua secondo
la radice quadrata della concentrazione dell'elettrolita. Questo fu dedotto
dalle proprietà di polarizzazione associate per cloridi disciolti
in acqua e metanolo. Per concentrazioni dell'ordine di 0,02 moli per litro,
la permettività relativa, per frequenze comprese tra i 5 ed i 20
MHz, risultava essere maggiore di quella del puro solvente. Per concentrazioni
maggiori, la permettività invece scendeva, in accordo stavolta con
tutte le precedenti misure riportate in letteratura. Fu presentata allora
una nuova teoria per tenere conto di questa diminuzione di permettività,
relativa alla "mancanza di polarizzazione cinetica". Secondo questa teoria,
il decremento dielettrico è legato a due effetti associati alla
migrazione degli ioni per la presenza di un campo elettrico applicato.
Un primo effetto è associato alla rotazione indotta dalle molecole
dipolari di solvente circostanti quando gli ioni si spostano, l'altro dipende
dal tempo finito necessario perché gli ioni raggiungano le loro
velocità d'equilibrio. La riduzione totale De
della permettività, dovuta a questi effetti si può determinare
con l'espressione:
De = ( es-e¥
)tss/e0es
( 1.12 )
dove es ed e¥
sono i valori limite per le basse e le alte frequenze relativamente al
solvente,t è il tempo di rilassamento
dielettrico del solvente puro e ss
è la conducibilità per basse frequenze della
soluzione elettrolita. Concordanze con la teoria sono state trovate per
soluzioni di metanolo, ma non per soluzioni acquose, probabilmente per
le troppe semplificazioni fatte. Oltre al cambiamento della permettività
delle soluzioni elettrolite in confronto al puro solvente, è stato
poi anche osservato un cambiamento per il valore del tempo di rilassamento
dielettrico. Per basse concentrazioni di elettrolita, infatti, il tempo
di rilassamento t varia linearmente con la concentrazione,
di solito diminuendo il suo valore. Si usa esprimere il decremento di t
mediante la lunghezza d'onda l corrispondente
alla frequenza ( 2pt )-1
cosicché:
l =l'
+ 2dlc,
( 1.13 )
dove
dl = ( dl++dl-
) / 2
( 1.14 )
Alcuni valori dei decrementi dell'onda per i vari ioni sono riportati in
tabella 5.
| Catione |
dl+ ( ±2
)*10-4m |
Anione |
dl- ( ±2
)*10-4m |
| H+ |
+4 |
OH- |
-2 |
| Li+ |
-3 |
Cl- |
-4 |
| Na+ |
-4 |
F- |
-4 |
| K+ |
-4 |
SO42- |
-11 |
| Mg2+ |
-4 |
I- |
-15 |
Tab.5
Si può pensare che il decremento del tempo di rilassamento rifletta
il grado di distruzione della struttura dell'acqua normale a causa degli
ioni solvati. Nel caso di acqua strutturata associata alle bioma-cromolecole
si ha dispersione dielettrica nella regione di frequenze comprese tra le
dispersioni relative al ghiaccio ed all'acqua. In effetti, Buchanan ed
altri hanno esaminato le proprietà dielettriche di soluzioni di
sei proteine alle frequenze comprese tra i 3 ed i 24 GHz. Estrapolando
i risultati per frequenze inferiori a quelle per cui si ha il rilassamento
dell'acqua normale, si notò come il valore della permettività
relativa fosse minore di quello dell'acqua normale. Questa differenza si
pensò che dipendesse dall'esistenza di acqua "irrotazionalmente
legata" alle molecole proteiche e, a seconda della forma di queste molecole,
la quantità di tale acqua legata fu valutata dell'ordine di 0,2-0,4
g di acqua per 1 g di proteine. Questi studi suggeriscono che una dispersione
dielettrica per l'acqua legata alle proteine avvenga a frequenze inferiori
a quelle relative all'acqua normale. Questa dispersione, indicata come
dispersione di tipo d, fu osservata da Schwan
per soluzioni di emoglobina e da Grant per soluzioni di albumina. La dispersione
d ha luogo per frequenze comprese tra il rilassamento
legato allo orientamento delle proteine (dispersione b
) e quello dell'acqua (dispersione g). In figura
13 abbiamo riportato lo spettro della dispersione dielettrica che si ha
per soluzioni acquose di proteine.
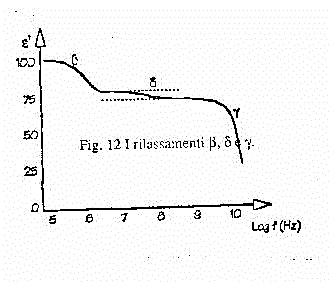Fig.13 - I rilassamenti
b,d e g
.
E' da notare che finora si sono considerate sempre proteine in polvere
piuttosto che in soluzione; questo per evitare le complicazioni relative
allo orientamento delle molecole proteiche così da poter studiare
più comodamente il comportamento delle molecole d'acqua. Attraverso
varie misure, condotte per frequenze comprese tra i 10 MHz ed i 25 GHz,
si sono trovati due centri distinti di dispersione, uno intorno ai 250
MHz, l'altro intorno ai 9,95 GHz. La prima dispersione la si associò
ad un primo monostrato fortemente legato di acqua assorbita, la seconda
ad un secondo strato d'idratazione meno fortemente legato; successive misure
confermarono il fatto che per le proteine idratate, la perdita dielettrica
per frequenze ai 10 GHz è associata all'acqua legata nei siti di
assorbimento secondari e, mediante studi sulle isoterme d'idratazione per
proteine a 9,95 GHz, si e' visto come la perdita dielettrica sia direttamente
proporzionale al contenuto d'acqua nelle zone d'idratazione secondaria.
Simili studi sono rilevanti anche per possibili applicazioni mediche,
riguardo, ad esempio, i pericoli legati a radiazioni a microonde o le ricerche
sui tumori. E' stato visto mediante N.M.R. che i tessuti tumorali mostrano
per il rilassamento associato agli spin dei protoni nel reticolo dell'acqua,
valori maggiori di quelli che si hanno per i normali tessuti. Inoltre le
cellule tumorali, normali o trasformate mediante virus, mostrano differenze
di assorbimento alle microonde. Oltre a questi studi sul rilassamento dielettrico
dell'acqua legata a molecole proteiche, posso considerare, accanto alle
proteine, altre molecole o polimeri; si è trovato che i tempi di
rilassamento per l'acqua legata a queste nuove biomolecole hanno valori
circa a metà tra quelli dell'acqua normale e quelli del ghiaccio
a 25 °C, con una tendenza ad avvicinarsi a quelli dell'acqua liquida.
Nella tabella 6 si hanno degli esempi relativi a quanto detto.
| Molecola |
t( sec.) |
Note |
| Emoglobina equina |
2*10-10 |
soluzione,22%, 25°C |
| Lisozoma |
5*10-10 |
polvere,33% H2O, 25°C |
| Albumina nel siero bovino |
1.6*10-9 |
soluzione1%, 25°C |
| Albumina nell'uovo |
5.3*10-10 |
soluzione1%, 25°C |
| Amido |
(a) 1*10-9
(b) 2*10-10 |
polvere,25°C
(a) 15% H2O,(b) 20% H2O |
| D-glucosio |
2*10-10 |
soluzione 2 moli, 5°C |
| Acqua liquida |
8.2*10-12 |
25°C |
| Ghiaccio |
2.810*-5
2.4*10-6 |
-3.8°C
estrapolato a 25°C |
| Prolina,idroxiprolina,acido e-amino-n-caproico |
~1*10-10 |
soluzione 2 moli, 20°C |
Tab.6
Note
12 - Utilizzando tecniche di purificazione
basate sull'esclusione di ioni per via elettroforetica.
13 - Il moto Browniano è un movimento
irregolare e casuale delle particelle di un generico fluido, conseguenza
dell'agitazione termica. Si propaga per fluttuazioni statistiche di pressione
alla superficie delle particelle.
14 - Dipenderà dunque dalle caratteristiche
della funzione di distribuzione utilizzata per l'analisi. Viene, in genere,
utilizzata la distribuzione gaussiana in quanto modella meglio questi fenomeni.
15 - Si sceglie quindi come valore per
a 2,76 Å .