2.5 - Tessuti a
medio contenuto di acqua : tessuti soffici
Il corpo umano è fondamentalmente composto da tessuti a medio
contenuto d'acqua, e cioè proprio da muscoli e tessuti soffici (gli
organi internidell'uomo possono essere tutti, in prima approssimazione,
messi in questa categoria). Ecco perché consideriamo due tipi di
per una medesima categoria. L'analisi è particolarmente importante
proprio perché s'inseriscono all'interno di questo gruppo anche
le cellule ed i tessuti tumorali. Un'approfondita conoscenza delle caratteristiche
dielettriche di questi tessuti può dunque permettere, in alcuni
casi, la messa a punto di tecniche di cura e di diagnosi.
2.5.1 - Dispersione alfa
Si ha un andamento analogo a quello della dispersione nel muscolo.
2.5.2 - Dispersione beta
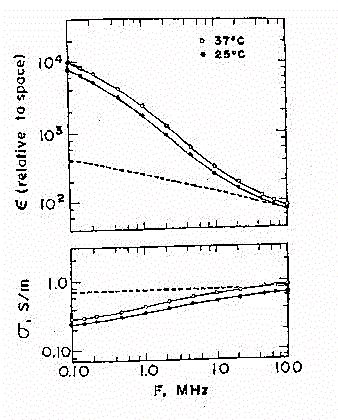Fig.34
Nella figura 34 e' illustrata la permittività e conducibilità
del pancreas di cane. La linea trattegiata dà le misure per il materiale
omogeneizzato. Si noti come il rilassamento sia meno pronunciato. I parametri
(in parentesi i valori a 37 °C) sono: eo
= 10,480 (12,960); e¥
= 41,3 (36,7); ss =
0,226 (0,268) S/m; fc = 230 (254) kHz;
a = 0,232 (0,228) Si osservi la figura 34. Sono
graficati i risultati di misure sperimentali a 25 °C e 37 °C sul
pancreas di un cane, trattando poi i risultati ottenuti con un fitting
alla Cole-Cole. La prima cosa che si nota è che non ci sono grandi
perdite, e quindi grandi variazioni, né per s
né per e . Il fenomeno di rilassamento,
e le perdite correlate, sono in questo caso dovute alla presenza delle
cellule. Le cellule presenti in questi tessuti hanno caratteristiche variegate,
e la loro diversità, soprattutto per le di dimensioni delle loro
membrane, genera l'ampia distribuzione del fenomeno, pari a circa tre decadi.
La linea tratteggiata rappresenta un tentativo di omogeneizzazione del
tessuto, in modo da lasciare inalterato il materiale dal punto di vista
dielettrico, ma facendo scomparire la struttura organizzativa cellulare.
Ciò significa tener conto della presenza dei diversi materiali,
ma supporre l'assenza totale di cellule. Avremo dunque valori molto più
bassi per le basse frequenze; è quindi qui che la membrana dà
il suo massimo contributo alle caratteristiche dielettriche del tessuto.
Quello che si ottiene è una discrepanza nei valori del materiale
omogeneizzato che diventa considerevole alle basse frequenze, dove la presenza
delle membrane cellulari è fondamentale. Il che porta a concludere
che questa dia un grosso contributo alla conducibilità ed alla permettività
a queste frequenze. Un'ulteriore conferma dell'influenza della membrana
si può averla andando ad osservare l'andamento alle frequenze intorno
ai 100 MHz. Qui, dove le membrane cellulari divengono trasparenti (usando
ancora l'analogia con i condensatori, sono "cortocircuitate"), si ha un
ottimo accordo con i dati sperimentali fittati alla Cole-Cole. La frequenza
di rilassamento è intorno ai 200 kHz. Il fenomeno è però
piuttosto distribuito in frequenza e non si ha dunque una sola costante
di tempo (alla Debye), ma svariate. Ciò ha condotto alla formulazione
del modello di Stoy:
e'r = Si
Dei / [ 1+ ( f / fci
)2 ] + e¥
( 2.6 )
In sostanza, quello che si fa, è spezzare il comportamento alla
Cole-Cole in tanti sotto fenomeni alla Debye. Si è inteso con e¥
il contributo dato dalle proteine in soluzione acquosa a 100 MHz, e con
Dei ed fci,
rispettivamente, l'aumento di permettività e la frequenza centrale
di rilassamento della i-ima struttura. Osservando dall'esterno, non si
riscontra un andamento netto, ma un allargamento di banda e fenomeni poco
definiti, ma separati; si preferisce allora studiare non il tutto nel suo
complesso, ma studiare separatamente e poi sommare i diversi contributi,
con una media pesata in cui si tenga conto della frazione di volume di
ognuno di questi.
| Struttura |
Raggio medio ( m ) |
% volume |
De |
fc ( MHz ) |
| Epatocito |
8.9*10-6 |
83% |
9400 |
0.72 |
| Nucleo |
3.9*10-6 |
5% |
470 |
1.6 |
| Mitocondrio23 |
5.0*10-7 |
22% |
277 |
13 |
| Reticolo endoplasmatico24 |
2.5*10-8 |
15% |
8 |
250 |
| Proteine25 |
|
16% |
100 |
3 |
Tab.9
Nella tabella 9 si vede come si procede operativamente alla suddivisione
del tessuto complessivo nei singoli contributi.
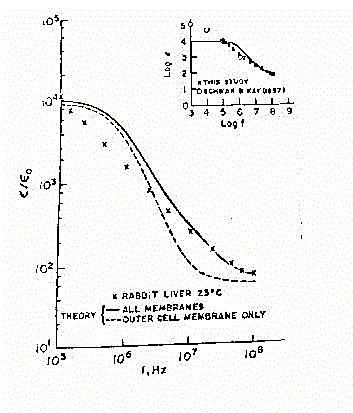Fig.35
In figura 35 e' illustrato l'andamento della permittivita' calcolata
e misurata per il fegato di coniglio.Si noti come i valori sperimentali
(le crocette) siano in buon accordo sperimentale, specie alle alte frequenze
con la teoria, in particolare se si considera l'intero sistema di membrane
invece che solo la membrana delle cellule esterne.Si noti inoltre come
la permittivita' totale predetta con l'utilizzo di questo semplice modello
aderisce bene ai risultati sperimentali intorno ad 1 MHz ed un po' meno
a frequenze minori. La linea tratteggiata indica la previsione tenendo
conto della sola parte esterna della membrana, mentre quella continua considera
la membrana interamente. Fisicamente, quello che accade è che, alle
basse frequenze la parte interna della cellula è schermata dal campo
elettrico esterno proprio dalla membrana, e quindi il materiale cellulare
al suo interno non contribuisce alla permettività totale. D'altra
parte, non contribuiscono nemmeno ad alte frequenze perché in quel
caso le membrane sono "cortocircuitate". Esiste dunque un intervallo piuttosto
limitato di frequenze in cui la carica della membrana subcellulare contribuisce
significativamente alla permettività del tessuto: dalla frequenza
di rilassamento b della cellula complessiva,
fino a quella del materiale intracellulare. Il rapporto di queste due frequenze
è funzione delle dimensioni delle membrane esterne e del singolo
materiale intracellulare.Anche se l'analisi di Stoy è molto approssimativa
conduce alle seguente conclusioni:
1 - La dispersione dielettrica nell'intervallo da 1 a 100 MHz rappresenta
la funzione in alta frequenza della dispersione di tipo b
delle cellule con tutti i suoi "organi" interni.
2 - La variabilità delle dimensioni delle strutture legate alle
membrane nel tessuto spiega l'ampio range della frequenza di rilassamento
osservato alle RF26.
3 - Il valore della permettività osservato al di sotto di 105
Hz (basse frequenze) è maggiore di quello che ci si attende considerando
la sola polarizzazione delle cellule.
4 - Il contributo delle proteine è, alle RF, piccolo in confronto
a quello della membrana.
2.5.3 - Dispersione gamma
Il contributo dell'acqua alla permettività può essere
rappresentato (alle frequenze delle microonde) al di sopra dei 5 GHz con
l'equazione di Debye assumendo la frequenza di rilassamento identica a
quella dell'acqua ( vedi figure 18 e 19 ) e scegliendo arbitrariamente
e¥ = 4.
Il valore che si ottiene dal fitting per es
(indicato con un pedice m in figura 31 ed in tabella 10) è
all'incirca uguale al contributo dell'acqua alla permettività
a frequenze al disotto di 1 GHz. I valori di conducibilità di questi
tessuti a 100 MHz approssimano quella del citoplasma in assenza della
membrana. I parametri riscontrati sono tutti riassunti
nella tabella 10.
2.5.4 - Dispersione delta
Il fenomeno di rilassamento, alle microonde, è molto più
esteso di quanto ci si aspettidalla sola acqua. La dispersione d
(senza "contare" l'acqua libera) si allarga fino alla regione delle RF.
Si è cercato di calcolare i parametri di alcuni tessuti sani e di
alcuni tessuti malati.
| Tessuto |
Simbolo riferito alla figura 37 |
Frazione di volume d'acqua
1-p |
Permittivita' estrapolata per le microonde
ems |
Conducibilita' a 0.1 GHz
s0.1
S/m |
Conducibilita'estrapolata per le microonde
s0.1 S/m |
| Materia grigia |
D |
0.84 |
44 |
0.70 |
1.13 |
| Materia bianca |
s |
0.74 |
34 |
0.48 |
0.75 |
| Ematoma splenico ( due campioni ) |
m
m |
0.86
0.795 |
47
47 |
0.92
0.85 |
1.60
1.30 |
| Muscolo |
n |
0.795 |
47 |
0.70 |
2.40 |
| Emangiopericitoma ( due campioni ) |
x
( |
0.91
0.92 |
53
58 |
1.16
1.37 |
2.90
3.60 |
| Grasso |
Ñ |
0.09 |
10 |
0.005 |
0.10 |
| Leiomiosarcome intestinale |
l |
0.87 |
53 |
1.05 |
2.30 |
| Fegato |
o |
0.795 |
43 |
0.67 |
2.30 |
| Fibroleiomioma vaginale |
; |
0.87 |
59 |
non misurato |
1.80 |
| Adenosarcoma papillare del polmone |
) |
0.84 |
51 |
non misurato |
1.40 |
| Lipoma |
t |
0.28 |
20 |
non misurato |
0.40 |
| Adenosarcoma tubolare del rene |
|
0.84 |
50 |
non misurato |
2.40 |
Tab.10
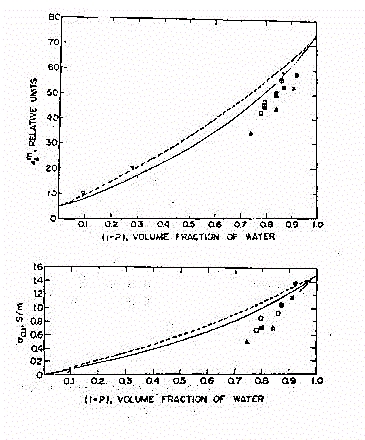Fig.36
Nella figura 36 possiamo vedere le caratteristiche dielettriche di
tessuti tumorali. I dati della permittività sono stati estrapolati
per tessuti tumorali e tessuti normali per frequenze oltre i 3 GHz, tramite
l'equazione di Dbye con una frequenza di rilassamento pari a quella dell'acqua.
Quelli sulla conducibilità sono stati ottenuti per una frequenza
di 100 MHz. Nei grafici riportati in figura 36 ci sono i valori previsti
per es e s
al variare della frazione di volume d'acqua. La linea tratteggiata indica
le previsioni della teoria di Maxwell-Fricke (sfere sospese in soluzione);
la linea continua quelle della teoria di ellissoidi con rapporto assiale
5:1 in sospensione. I diversi simboli indicano i valori di es
e s (a 100 MHz) dei diversi tessuti già
riportati in tabella. E' necessario provare a dare una definizione di cosa
s'intenda con "tessuti malati". Stiamo parlando di tessuti e cellule tumorali
e si tratterà di definire quale possano essere effettivamente le
differenze tra queste cellule e delle cellule sane. Il tumore è
una malattia causata da una crescita incontrollata delle cellule, la cui
causa è il risultato di interazioni con fattori ambientali, genetici,
metabolici. Le peculiarità di una cellula tumorale sono riassumibili
in quattro punti:
1. Clonalità: da un'unica cellula mutata si hanno, per clonazione,
molte cellule mutate;
2. Autonomia: la crescita è indipendente, in numero e modalità,
dai normali processi biochimici ed ambientali;
3. Anaplasia: non si presenta una differenziazione cellulare coordinata;
4. Metastasi: è indubbiamente il passo più pericoloso
per l'uomo, ed è la capacità delle cellule tumorali di avere
una crescita
disomogenea ed una proliferazione anche a distanza, in distretti dell'organismo
diversi da quelli in cui si verifica la trasformazione della cellula originale.
Ciò che si sa certamente, è che le cellule tumorali tendono
a ritenere al loro interno una grossa quantità d'acqua. Questo comporta
caratteristiche dielettriche diverse rispetto ai tessuti sani, soprattutto
alle basse frequenze.
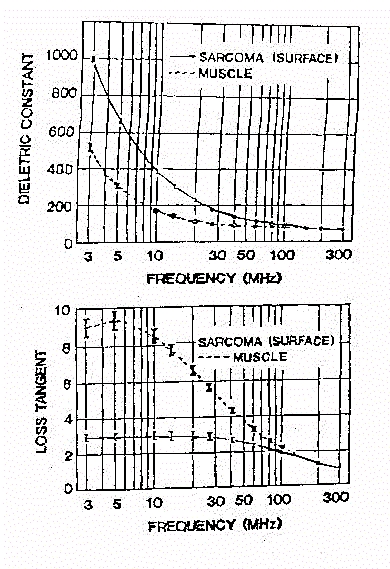Fig.37
Si vede, dalla figura 37 il diverso comportamento del muscolo rispetto
al sarcoma (forma tumorale) localizzabile maggiormente alle basse frequenze.
A 10 MHz abbiamo per le cellule tumorali un valore di e'
doppio rispetto al muscolo. La diversità tra i due tessuti può
essere messa in evidenza anche in termini di tangente di perdita, mostrando
come la conducibilità di questi tessuti
tumorali sia notevolmente maggiore di quella del muscolo in condizioni
normali. Ciò permette un facile scorrimento della
corrente all'interno delle cellule.Si è poi scoperto che le
cellule tumorali sono molto sensibili a temperature piuttosto elevate,
mentre lo sono meno alle variazioni di temperatura. Sperimentalmente è
stato visto che, un tessuto sano a 43 °C, risente meno di uno malato
ed è più resistente. Queste considerazioni sono alla base
dello sviluppo dell'ipertermia. Scaldando tutto il tessuto alla frequenza
delle microonde, infatti, la parte malata sente maggiormente gli effetti,
e la terapia è indubbiamente più localizzata. Un'altra tecnica
nota è l'elettroterapia, che utilizza l'elevata conducibilità
e la scarsa resistenza al calore nel tentativo di curare i tumori. Si usano
due elettrodi e con una modalità leggermente invasiva si fa scorrere
della corrente che, per effetto Joule, riscalda i tessuti ed insidia maggiormente
quelli malati. I risultati sembrano essere buoni. La conoscenza delle caratteristiche
dielettriche può essere sfruttata anche nel campo della diagnostica
per rilevare la presenza di tumori. Si usano delle antenne all'esterno
del soggetto, s'invia un segnale e si analizzano i valori di costante dielettriche
e di sfasamento che si riscontrano, ripetendo il processo con segnali ed
antenne con angolazioni diverse. In questa maniera si cerca di determinare
se nella zona in esame siano o meno presenti delle cellule con un comportamento
differente da quelle sane. Si cerca, in sostanza, di risalire dalle informazioni
sulle riflessioni alla natura della cellula usando tecniche di telerilevamento.
Il problema è che nel telerilevamento ci si trova di fronte a superfici,
mentre qui si ha a che fare con volumi e si hanno quindi problemi tecnici
non indifferenti. Obbiettivi da raggiungere sono:
- Una buona focalizzazione del campo per poter circoscrivere l'azione
curativa della tecnica;
- Elevata risoluzione per la diagnosi di eventuali cellule tumorali.
Avremmo dunque bisogno di lavorare con piccole lunghezze d'onda e quindi
alte frequenze. Però:
- Alle alte frequenze gran parte della potenza del segnale non penetra
nel tessuto ma resta in superficie, e quindi la diagnosi o la cura in questo
caso funzionano se il tumore non è profondo (come può essere
il melanoma della pelle)
- In questo range le differenze di comportamento fra tessuto sano e
cellule tumorali s'attenuano notevolmente e quindi la tecnica è
di difficile applicazione.
Note
23 - I mitocondri sono di forma cilindrica,
di diametri 2,4 e 0.6 mm.Il raggio medio e'
stato calcolato come quello di una sfera equivalente in volume
24 - Il raggio medio e' stato preso pari
alla meta' dell'ampiezza media del "contenitore" del reticolo
25 - Si e' supposto che il tessuto proteico
abbia una permittivita' statica ed una frequenza di rilassamento tipica
della maggior parte delle proteine globulari. E sebbene questi valori non
siano certi per la maggior parte dei tessuti proteici fibrosi, ad ogni
modo il loro contributo all'incremento dielettrico complessivo e' probabilmente
minore, a tutte le frequenze, di quello dovuto alla polarizzazione della
membrana.
26 - RF sta per Radio Frequenze, ovvero
le frequenze comprese tra 100 kHz e 300 MHz, generalmenta usate per radiocomunicazioni.