2.Materiali biologici

Indice Capitolo2


2.1 - Generalita'

La presenza dell'acqua nei tessuti biologici dà luogo a proprietàcaratteristiche che possono essere messe in evidenza in vari
modi. Consideriamo ad esempio le conducibilità dei vari tessutibiologici riportate in tabella; si può vedere come i valori siano fortemente diversi tra materiale e materiale. Si vedrà poi come e quanto le differenze dipendano proprio dalle diverse percentuali d'acqua contenute nel materiale che si prende in considerazione (i valori sono considerati ad una frequenza di 100 MHz e 3 GHz).
 

f ( Mhz ) Muscolo Fegato Polmoni Milza Rene Materia bianca Materia grigia Osso Sangue Grasso
100 0.9 -0.08 0.7 0.53 0.75 0.68 0.45 0.7 0.0574 1.0 0.02
3000 2.8 2.8 - 2.7 2.3 1.5 2.0 0.16 2.7 0.04
Tab.7

L'importanza di quest'aspetto nello studio dell'interazione tra campi elettromagnetici e tessuti biologici è messa poi in evidenza anche dalle differenze che si riscontrano con misure tramite il modello a 180 celle utilizzato con la tecnica FDTD qualora le celle vengano considerate omogenee per caratteristiche dielettriche, o vengano piuttosto valutate con le loro effettive costanti, a seconda del materiale maggiormente presente nella porzione di "corpo" simulato dalla cella.
 



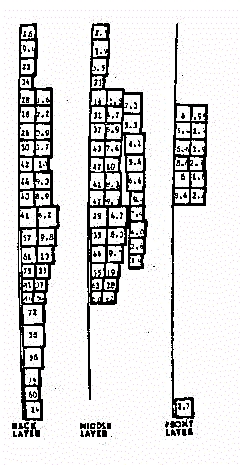
Fig.14 - Modello a 180 celle disomogeneo


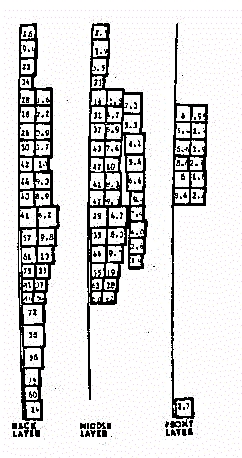
Fig. 15 - Modello a 180 celle omogeneo

 
Nel primo modello si ha una migliore caratterizzazione dei tessuti in quanto ad ogni cella vengono assegnate le caratteristichedielettriche del materiale percentualmente più determinante. Si noti ad esempio come ci siano maggiori dislivelli nei valori di SAR a livello della coscia, dove, nella prima modellizzazione si e' tenuto conto della maggiore presenza di tessutomuscolare, rispetto al resto della gamba, dove predomina la presenza dell'osso.
Guardando i risultati sia sperimentali che tramite modelli si vede come, aldilà di eventuali fenomeni di risonanza, la maggiore potenza assorbita si ha nei tessuti a più alto contenuto d'acqua, secondo lo schema di fondo :

CONTENUTO DI H2O Þ MAGGIORE CONDUCIBILITÀ Þ MAGGIORE POTENZA DISSIPATA ALL'INTERNO.

2.2 - Proprietà dielettriche dei materiali biologici

Procediamo dunque ad una suddivisione in tre gruppi principali. Tutti i materiali all'interno di uno stesso gruppo sono caratterizzati da una simile percentuale d'acqua e quindi l'andamento della permittività e della conducibilità è analogo.
 
Contenuto d'acqua Caratteristiche
Maggiore dell'80%  In questa categoria sono inclusi tutti i fluidi con elettroliti, macromolecole e materiale cellulare poco aggregato. Le cellule sono a grande distanza e sono libere di muoversi nell'acqua che le circonda. 
Esempi caratteristici sono: il fluido cerebrospinale, il sangue e l'umore vitreo. 
Abbiamo considerato l'occhio poiché il suo umore acqueo (contenuto nella camera posteriore ed anteriore. Numero 3 in figura 16) è essenzialmente una soluzione d'acqua e sali disciolti, e il corpo vitreo (numero 4 in figura 16) è una massa "gelatinosa" composta da una particolare soluzione salina. 
Minore dell'80% In questo gruppo rientrano la pelle, i muscoli, la materia grigia e la maggiorparte degli organi interni 
(fegato, milza). Per i polmoni si ha un comportamento diverso poiché contegono aria al loro interno. 
 Minore del 40% Sono fondamentalmente ossa, tendini e grasso caratterizzati da bassa costante dielettrica, bassa 
conducibilità e ridotto contenuto d'elettroliti. 
Mentre per gli altri materiali non si apprezzano notevoli differenze nelle caratteristiche e nella 
composizione, al variare della specie animale da cui si prelevano i campioni, per il tessuto grasso si hanno valori d'acqua che spaziano dal 2% fino a più del 40%.Otteniamo quindi valori per la costante dielettrica e per la conducibilità diversi a seconda della specie considerata. 
Tab.8
 
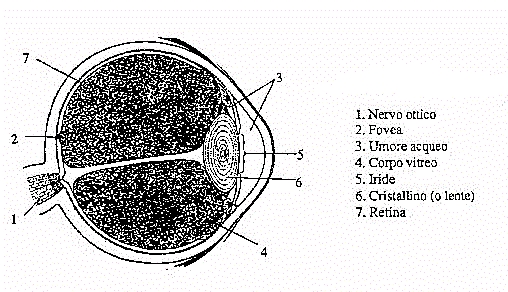Fig.16 - L' occhio umano
 
Prima d'analizzare nello specifico le caratteristiche di questi tre gruppi, vediamo quali sono i diversi contributi in termini di e e di s al variare della frequenza.

2.2.1 - A bassa frequenza ( fino a 100 khz )

La permettività puòraggiungere, in questo range di frequenze, valori di 106. Si ha in questa zona la presenza di tre fenomeni.
1- Il primo, ed il predominante, è l'effetto dovuto alla presenza di elettroliti in soluzione (conducibilità ionica). Si ha spostamento delle cariche,che muovendosi nel fluido extracellulare, e più raramente, in quello intracellulare, danno un notevole contributo di perdite (vedi figura 17) .
 

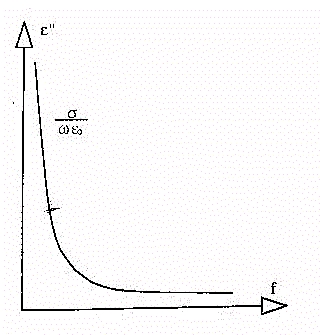Fig.17 - Perdite da conducibilita' ionica
 
2- Si ha il contributo di rilassamento dovuto a polarizzazione da interfaccia. Questo si verifica in soluzioni cellulari, ela frequenza di rilassamento sarà funzione delle dimensioni delle cellule e dello spessore della loro membrana. Usando la schematizzazione circuitale già analizzata16, di un condensatore per la membrana, si ricorda che il fatto d'avere una membranamolto sottile ed una grossa carica affacciata sulla superficie dà un alto valore per la capacità, e di conseguenza, per la e16.
3. Un terzo fenomeno è dovuto alla carica presente sulla superficie della membrana che instaura una polarizzazione da controioni16.Questo fenomeno è il primo che si realizza, ed è il maggiore responsabile della diminuzione di e. Questo significa un aumento di e",(una dispersione), e conseguentemente, un rilassamento, che si definisce rilassamento di tipo a. Ovviamente, a seconda del materiale, avremo diverse frequenze di rilassamento (brevemente indicate con fc). La variazione di conducibilità dovuta al rilassamento di tipo , deve confrontarsi in questo range di frequenze, con l'andamento della conducibilità trattato al primo punto.Supponendo una variazione complessiva De di 106, ed una fc ~100 Hz, ci si aspetta un aumento di conducibilità (tramite le formuledi Kramers-Kronig) pari a 0,005 S/m dovuto alla dispersione a. I valori per la conducibilità ionica possono essere calcolati tramite le formule di Maxwell-Fricke nel caso del sangue, il che è possibile per l'ipotesi di una membrana molto sottile rispettoal volume occupato dal fluido extracellulare. I calcoli sono stati effettuati utilizzando un fattore di forma g variabile tra 0,65 ed1,39 (conseguenza delle diverse forme e dimensioni degli aggregati molecolari nel sangue)17.
Considerando una conducibilità ionica per i normali fluidi biologici pari a 2 S/m, ed una percentuale di fluido extracellulare per i tessuti solidi dell'ordine del 10%, se ne ottiene un valore di conducibilità alle basse frequenze di 0,14 S/m. Si vede come questi valori siano notevolmente maggiori di quelli dovuti alla dispersione a, rendendo questa dispersione di scarsa importanza dal punto di vista ingegneristico.

2.2.2 - A media frequenza ( fino a 300 Mhz )

Salendo in frequenza, la membrana, schematizzata con un condensatore, si può considerare come cortocircuitata e si puo'
dunque applicare la teoria delle misture, considerando le proteine contenute all'interno della cellula. Queste intervengono determinando il cosiddetto rilassamento b. La differenza rispetto alla dispersione di tipo a è che l'effetto della conducibilità ionica è meno influente di quella dovuta alla presenza di proteine nella soluzione. Questo perché il valore di w è maggiore e quindi il termine s/we diminuisce d'importanza. In questo range di frequenze la curva della conducibilità ionica presenta delle variazioni minime al variare della frequenza, e può quindi quasi ritenersi costante. Per quanto riguarda e", invece, sperimentalmente si nota che si ha una frequenza di rilassamento fc intorno ai 500 kHz. Vediamo allora una schematizzazione grafica dei vari contributi.
 

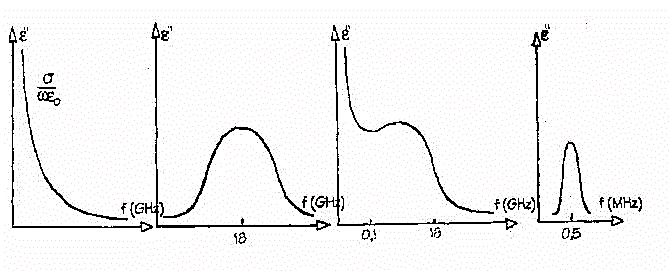Fig.18
 
Nel primo grafico in figura 18 abbiamo riportato l'andamento della conducibilità ionica, nel secondo l'andamento dell' acqua pura , nel terzo quello di una soluzione salina, ottenuto come somma dei primi due. Il quarto grafico rappresenta la dispersione di tipo b, che a causa della bassa frequenza di taglio, è stata diagrammata su una scala in MHz invece di una in GHz. Vediamo ora la composizione del terzo e quarto grafico, che descrive l'andamento totale di una soluzione acquosa alle medie frequenze.
 
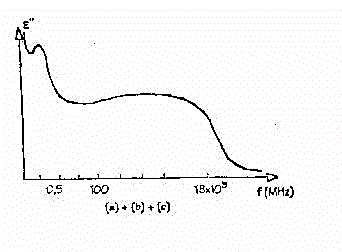Fig.19 - Andamento complessivo
 
Si noti che questo grafico va ben oltre le medie frequenze. La prima brusca variazione è dovuta al rilassamento di tipo b, mentre il minimo relativo che si sperimenta intorno a 100 MHz è dovuto all'effetto combinato della conducibilità ionica e di quella dell'acqua pura. Il comportamento oltre queste frequenze è dovuto al rilassamento dell'acqua pura.
Si nota che l'andamento intorno ai 100 MHz riporta una notevole flessione del valore di e", al punto da presentare un minimo. Questo perché fino a questa frequenza la conducibilità ionica prevale sull'andamento dovuto all'acqua pura, facendo così diminuire il valore complessivo di e". Oltre il comportamento s'inverte, le perdite date dal rilassamento dell'acqua sono maggiori e determinano l'andamento generale anche salendo in frequenza.
Inoltre si fa notare come, se non ci fosse il rilassamento di tipo b, avremmo, alle medie frequenze, un andamento pressoché costante, poiché, a queste frequenze, i due andamenti si compensano.

2.2.3 - Ad alta frequenza ( UHF e m-onde , oltre i 100 Mhz )18

In questo range di frequenze abbiamo tre fenomeni:
1- Tra gli elettroliti in soluzione e le molecole di proteine, che sono poco
conduttive, si genera una polarizzazione da interfaccia (alla Maxwell-Wagner). E' particolarmente visibile solo in alcuni materiali, mentre generalmente si hanno valori di poche centinaia di mS/m. La frequenza di rilassamento che si sperimenta è comunque
intorno ai 300 MHz.
 

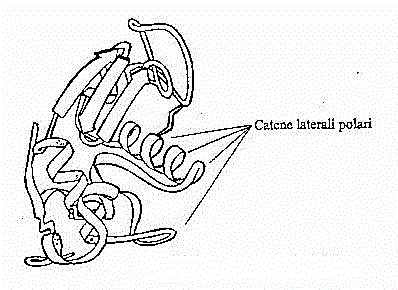Fig.20 - Modello a nastro di una proteina
 
2- Si possono avere perdite dovute a piccole molecole polari, come degli amminoacidi in soluzione, oppure dovute alle catene laterali polari di proteine (vedi figura 20). Avremmo, viste le minori dimensioni in gioco, frequenze di rilassamento ben oltre i 100 MHz, dove si centra invece il rilassamento dovuto alle intere catene proteiche. In realtà quest'ultimo contributo determina l'andamento medio e la fc rimane intorno ai 100 MHz.
3- Abbiamo poi il contributo dovuto al rilassamento dell'acqua pura, caratterizzato da un processo che presenta una singola
costante di tempo t pari ad 8 psec, a cui corrisponde una frequenza di rilassamento pari a ~20 GHz a 25 °C.
Per frequenze f << fc possiamo assumere, per la conducibilità s, una dipendenza dal quadrato della frequenza. Si veda la formula:
s = [2pf2 ( es-e¥ )e0 / fc ] / [1+ ( f/fc )2]                              (2.2)
 
Alle basse frequenze il denominatore si approssima ad uno, e rimane la sola dipendenza quadratica del numeratore. L'andamento asintotico tende invece ad un valore costante, come prevedibile da considerazioni fisiche sulla mobilità. Per tessuti ad elevato contenuto d'acqua, nel range di frequenze tra 3 e 5 GHz, quest'aumento di conducibilità è dello stesso ordine di grandezza di quella ionica. Questa compensazione genera un andamento costante nell'intervallo di frequenza (vedi figura 19). Inoltre la conducibilità dei tessuti e delle soluzioni proteiche, includerà il contributo del rilassamento dipolare dell'acqua legata, indicato come rilassamento di tipo d, con una fc di circa un ordine di grandezza minore di quella dell'acqua libera. La conducibilità totale è dunque definita da tre contributi:
- conducibilità ionica;
- rilassamento dovuto all'acqua legata;
- rilassamento dovuto all'acqua libera.
Sperimentalmente, però, sono tutti compresi tra 3 e 5 GHz, e non è sempre semplice separare le singole componenti.
Complessivamente possiamo osservare le caratteristiche dei tessuti con acqua comparando i dati sperimentali con quelli previsti nel caso di un rilassamento modellizzato con una sola costante di tempo. Si può rappresentare la conducibilità come la somma
di un termine dipolare e di uno ionico:
s = [2pf2 ( es-e¥ )e0 / fc ] / [1+ ( f/fc )2]  + ss                          (2.3)
 
in cui i parametri es,e¥ ed fc si riferiscono all'acqua pura (contributo dipolare) e  ss  alla conducibilità ionica. Supponendo le proteine non conduttive, possiamo riscrivere l'equazione per la conducibilità ricavata dalla teoria delle misture, nel caso di si << sa:
s ® ( 1-r' )sa / ( 1+r'/2 ) + 9r'si / ( 2+r' )2                     (2.4)
 
dove si  è il contributo di conducibilità del sistema proteine-acqua legata, e p' è la frazione di volume delle proteine disciolte in soluzione. Questa frazione è maggiore di p (frazione di volume delle proteine non idratate). La differenza (p' - p) indica la percentuale d'acqua a mobilità ridotta. Se si sceglie una frequenza sufficientemente elevata, le variazioni di  si   diventano
trascurabili, e la dipendenza di s dalla frequenza riflette quella di sa. In sa il contributo ionico è a sua volta trascurabile rispetto a quello dipolare, e ci confrontiamo ancora una volta con la prima equazione scritta per s, ovvero una funzione lineare di f2 / [1 + (f / fc)2] qualora fc sia quella della maggiorparte del liquido. Dopo questa discussione sui fenomeni che intervengono alle varie frequenze, analizziamo ora le caratteristiche dielettriche dei tre gruppi di tessuti che si erano prima distinti.

Note

16 - Stiamo cioè considerando una situazione del tipo:
 

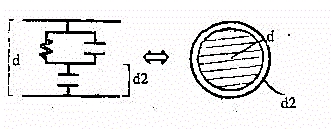Fig.21
 
Considerando il materiale interno dissipativo e quelo esterno non conduttivo, alle basse frequenze si avrà per la permittività la formula:
es = e2d / d2                                    ( 2.1 )
17 - La teoria utilizzata mantiene la sua validità anche per tessuti solidi, ma i risultati sono di più difficile predizione a causa della
maggiore complessità strutturale. Viene comunque simulata sufficientemente bene con la teoria delle misture.
18 - Si noti come le fasce in cui abbiamo suddiviso le frequenze non siano troppo stringenti, e si possa quindi considerare alte frequenze già i 100 MHz.
 
 
 
Home Page Indice Indice Capitolo2