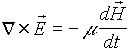
(2.1)
CAPITOLO 2
MODELLIZZAZIONE DEGLI ELEMENTI DEL SISTEMA
I metodi numerici permettono una valutazione teorica accurata della distribuzione del campo elettromagnetico nei diversi materiali dielettrici. Essi consentono di valutare molteplici situazioni di esposizione in maniera relativamente semplice. Esistono vari tipi di metodi numerici: il metodo delle differenze finite nel dominio del tempo (FDTD), il metodo dei momenti (MoM) ed il metodo degli elementi finiti (FEM).
Qui di seguito descriveremo brevemente FDTD, il metodo di gran lunga più utilizzato, ed il MoM.
2.1 Il metodo delle differenze finite nel dominio del tempo (FDTD)
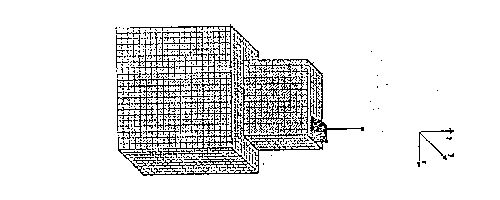
Il metodo FDTD si basa sulla soluzione, nel dominio del tempo, delle equazioni di Maxwell
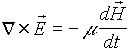
(2.1)
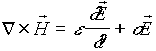
Esse si discretizzano nel dominio del tempo sostituendo ad ogni derivata il corrispondente rapporto incrementale. In questo modo le equazioni differenziali si trasformano in equazioni alle differenze finite; la loro soluzione consiste nella divisione della regione di analisi in una griglia di nodi <spazio, tempo>.
La cella elementare è quella di Yee, in cui la componente del campo elettrico è posta al centro del singolo spigolo, quella del campo magnetico al centro di ogni faccia, come evidenziato nella figura 2.1.
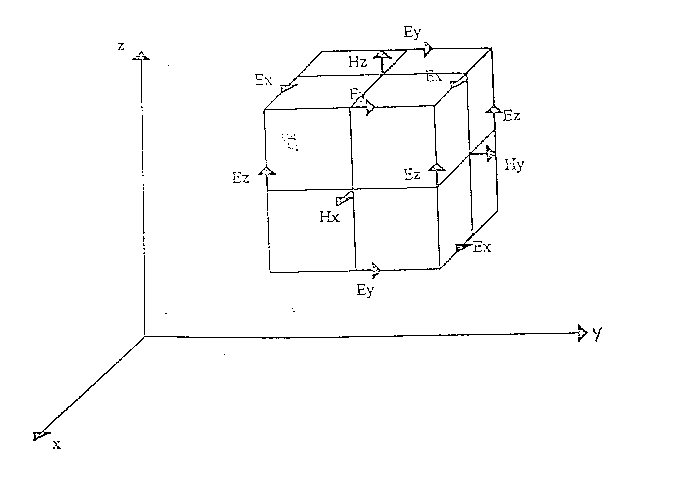
figura 2.1 - la cella elementare di Yee
Seguendo le notazioni di Yee ogni punto del dominio spaziale cartesiano discretizzato viene identificato dalla tripla
![]() (2.2)
(2.2)
dove Dx, Dy e Dz sono gli incrementi spaziali nelle rispettive direzioni coordinate; ogni funzione dello spazio e del tempo viene, inoltre, rappresentata nella seguente forma
![]() (2.3)
(2.3)
con Dt incremento temporale.
Grazie alla disposizione delle componenti del campo elettromagnetico nella cella di Yee si può utilizzare, per la definizione del rapporto incrementale, la formula alle differenze centrate
![]() (2.4)
(2.4)
raggiungendo, così, una precisione del 2° ordine.
Nella discretizzazione delle equazioni di Maxwell si sostituiscono. alle derivate spaziali e temporali, rispettivamente le seguenti espressioni
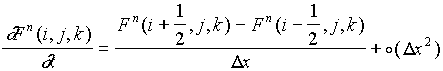 (2.5)
(2.5)
con le ovvie estensioni agli incrementi nelle direzioni y e z
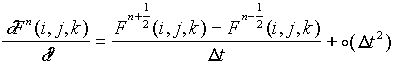 (2.6)
(2.6)
Poiché la singola componente del campo elettromagnetico in ogni cella è, in un certo istante, funzione di quelle relative alle celle adiacenti, calcolate negli istanti precedenti, si può risolvere il problema per approssimazioni successive.
L'elegante semplicità della tecnica FDTD, anche in casi di geometrie complesse in termini dielettrici, ne ha permesso la grande diffusione. A parità degli altri aspetti di calcolo si riesce, inoltre, ad ottenere un'accuratezza superiore unitamente ad una minore occupazione di memoria, rispetto agli altri metodi numerici.
Esistono, peraltro, degli svantaggi dovuti alla difficoltà del metodo a seguire i contorni geometrici della struttura in questione, agli errori di troncamento ed ai tempi di assestamento di soluzioni stabili e stazionarie.
2.2 Il metodo dei momenti (MoM)
Il metodo dei momenti può essere applicato a mezzi isotropi, non magnetici ed inomogenei. Il campo elettrico interno al corpo, E®, viene calcolato come soluzione dell'equazione integrale del campo elettrico ricavata dalle equazioni di Maxwell, data dalla
![]() (2.7)
(2.7)
Si suppone, infatti, che ogni elemento in cui è stato suddiviso il corpo, venga considerato sia come sorgente che come punto di osservazione. In questa ottica il campo incognito E® in ogni elemento è dato dalla somma del campo i-esimo, Ei®, presente in assenza del resto del corpo e dell'effetto di perturbazione, dovuto alla somma volumetrica di tutti gli altri punti che si comportano, a loro volta, come sorgenti.
Effettuando i calcoli su ognuno degli N elementi in cui viene suddiviso il corpo si ottiene un sistema di N equazioni vettoriali, quindi di 3N equazioni scalari, del tipo
![]() (2.8)
(2.8)
dove [A] è una matrice NXN di vettori. La soluzione di tale sistema si ottiene determinando gli autovalori di [A] e calcolando [Ei].
Particolare attenzione va rivolta alla modellizzazione della sorgente, visto che permette di valutare approfonditamente l'eventuale influenza, nel fenomeno della radiazione, del corpo (contenitore) del telefono; inoltre consente di studiare l'accoppiamento sorgente/testa dell'utilizzatore, sia in termini di conseguenze biologiche che di prestazioni di trasmissione; infatti, durante l'utilizzo, la testa del soggetto si trova in prossimità della sorgente radiante, modificando le caratteristiche radiative dell'antenna, con conseguenti degradazioni delle sue prestazioni e perdita di copertura nella direzione della testa. dotati di copertura nella direzione della testa . Generalmente gli apparecchi di telefonia mobile presenti sul mercato sono una sorgente radiante costituita, prevalentemente, da una antenna a stilo: questa è una scelta dettata dalla necessità di costruire dei sistemi radianti con caratteristiche di copertura sull'intero angolo azimutale (360°), nella gamma di 900 MHz, con larghezza di banda +/- 40 MHz; ulteriori vantaggi di questo tipo di antenna sono le sue dimensioni ridotte, il basso costo e l'estrema semplicità d'uso per l'utente comune.
Nella letteratura scientifica, ultimamente, il telefono cellulare viene simulato, relativamente alle sue proprietà radianti, da un dipolo a l/2 eccitato in tensione, oppure da un monopolo a l/4 alimentato in corrente. Il primo tipo di modellizzazione è adeguato a descrivere modelli di telefono MOTOROLA Classic: in questo apparecchio il radiatore risulta costituito da un cavo coassiale lungo l/2 sul quale, dal centro e per una lunghezza di l/4, è stata ripiegata la calza esterna metallica verso l'estremità inferiore; questo tipo di antenna, chiamato sleeve dipole (figura 2.2), equivale ad un normale dipolo a l /2 alimentato al centro.
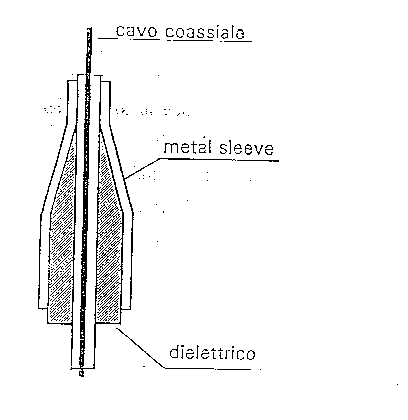
figura 2.2 - sleeve dipole
In esso il conduttore esterno di maggior diametro oltre a contribuire alla radiazione, essendo un ramo del dipolo, in condizioni di risonanza svolge la funzione di blocco della corrente di RF verso l'alimentazione.
Gli studi sperimentali condotti su sistemi sleeve dipole alla risonanza hanno evidenziato l'assenza di accoppiamenti apprezzabili tra il case e l'utilizzatore. Nonostante ciò, l'antenna sleeve dipole ha lo svantaggio di non poter essere collassata e questo la rende poco attraente per un utente che vuole disporre di un apparecchio dalle dimensioni contenute.
In figura 2.3 è fornito un confronto tra il modulo del campo magnetico emesso da un dipolo a l/2 ed il sistema "sleeve dipole + case", in una simulazione con metodo FDTD: possiamo notare, oltre alla somiglianza degli andamenti, l'effettiva scarsa capacità radiativa del case.
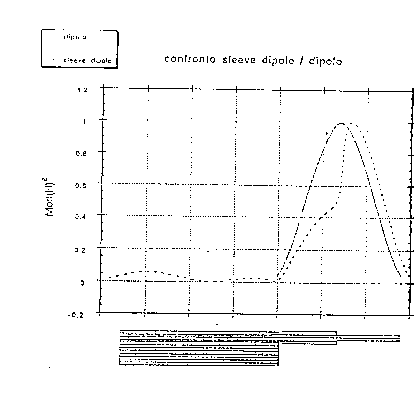
figura 2.3 - confronto 'sleeve dipole+case'-dipolo
Di seguito al Classic, tecnologicamente superato, sono comparsi sul mercato altri modelli di telefoni cellulari, che hanno sistemi radianti diversi dallo sleeve dipole; sfruttano, cioè, quelle caratteristiche delle antenne ad elica che, in impieghi a frequenze minori, consentono di evitare gli inconvenienti dovuti alle maggiori dimensioni dei dipoli a l/2 al crescere della lunghezza d'onda. Di solito, per i dispositivi di telefonia mobile, vengono utilizzati monopoli ad elica di lunghezza elettrico pari a l /4 e di lunghezza fisica l /12, avendo perdite sempre maggiori per dimensioni di antenna ancora minori.
L'impiego di questo nuovo tipo di antenne ha evidenziato che vengono eccitate anche intense correnti di RF che interessano il case, che diventa parte integrante del sistema radiante; infatti la parte del volto che si trova di fronte al case presenta i massimi valori di SAR di picco. Oltre al case anche la mano dell'utilizzatore, che lo sostiene, è interessata alle correnti di RF, comportandosi da dissipatore; la presenza della mano, peraltro, peggiora le prestazioni globali di trasmissione, per accoppiamento con il campo irradiato dall'antenna.
Per ovviare al difetto della struttura radiante ad elica singola, la perdita sensibile di guadagno in direzione della testa dell'utente, i telefoni cellulari attuali sono dotati di un impianto radiante costituito da due antenne ad elica: la prima, il radiatore primario, è l'antenna ad elica già descritta ed è l'unica operante quando la seconda è collassata nel contenitore del telefono, l'altra, il radiatore secondario, è formata da un'elica più stretta e di dimensioni elettriche l/2, con dimensioni fisiche di circa 10 cm, con, all'estremità superiore, 2 cm di dielettrico, per consentire, in caso di collassamento, la separazione elettrica con l'altra antenna, evitando così l'accoppiamento RF con essa e con il case. Quando non è l'unica antenna estesa il radiatore primario funge da trasformatore d'impedenza, consentendo l'adattamento tra il radiatore secondario e la linea di alimentazione collegata con il finale. Ovviamente, qualora il radiatore secondario fosse collassato, le prestazioni globali ottenute peggiorano, ricorrendo il difetto proprio dell'antenna ad elica unica a l /4; viceversa, quando il radiatore secondario viene esteso, il sistema radiante complessivo è simile ad un dipolo a 3l /4, opera in modo equivalente ad un dipolo a l /2 e, non essendo influenzato né dal case, né dalla mano dell'utilizzatore, evidenzia prestazioni soddisfacenti.
Le caratteristiche geometriche delle antenne descritte sono particolarmente adatte alla simulazione numerica FDTD; infatti (figura 2.4) per la modellizzazione di un dipolo che si estende lungo l'asse z, considerato idealmente infinitamente sottile, basta imporre l'annullamento delle componenti del campo elettrico tangenti al dipolo stesso ed imporre l'eccitazione al centro, nel gap di separazione del dipolo stesso.
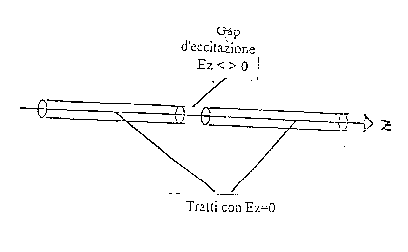
figura 2.4 - modellizzazione FDTD di un dipolo
Nella pratica questo avviene annullando la componente z del campo elettrico in tutte le celle in cui sono presenti fisicamente i conduttori che costituiscono l'antenna, esclusa quella centrale, corrispondente al gap tra i due rami del dipolo (figura 2.5).
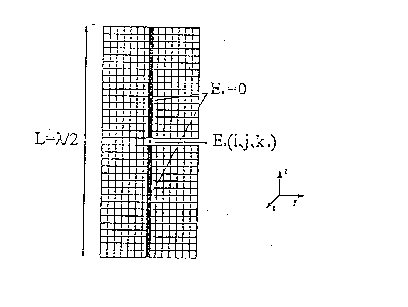
figura 2.5 - modellizzazione FDTD del campo elettrico emesso da un dipolo
Le altre componenti del campo sono ortogonali alla superficie del dipolo e vengono normalmente determinate con il metodo FDTD.
La sorgente viene alimentata con un'eccitazione di tensione ottenuta, nel caso del dipolo, imponendo un campo elettrico diretto normalmente alle superfici dei conduttori nella cella che divide i rami del dipolo e, nel caso del monopolo, imponendo il campo elettrico alla base e prendendo come riferimento di massa la parte metallica del case.
La potenza viene calcolata come prodotto dell'intensità del campo elettrico per le dimensioni della griglia, nuovamente moltiplicato per il valore della corrente che scorre, secondo l'asse z, nella cella di separazione tra i rami del dipolo. Questa corrente viene determinata grazie alla legge di Ampere di circuitazione del campo magnetico lungo il percorso costituito dai bordi della superficie, normale a z, della cella di separazione. Ragionando in modo analogo per tutte le celle costituenti la struttura.
I risultati che si raggiungono sono in buon accordo con i dati sperimentali, come si vede in figura 2.6, mostrando, ad esempio, per un dipolo a l /2 un andamento della corrente di tipo sinusoidale con il massimo posizionato al centro, dove si trova l'alimentazione dell'antenna.
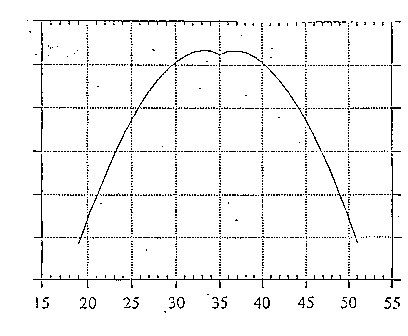
figura 2.6 - distribuzione della corrente nel dipolo (in ascissa si ha il n° di celle FDTD)
Questo modo di alimentare l'antenna equivale a considerare il campo elettrico impresso indipendente dalle condizioni esterne: si tratta di un'approssimazione che diventa grossolana nelle condizioni di esposizione in cui sono possibili fenomeni di accoppiamento: nel caso di un dipolo a l /2 la prossimità della testa all'antenna provoca, alla frequenza di risonanza, una diminuzione del modulo dell'impedenza di ingresso ed il modello descritto comporta un aumento della potenza irradiata. Si è, pertanto, introdotto un termine correttivo, indice del disadattamento di impedenza e, quindi, della potenza riflessa verso il generatore, per calcolare correttamente la potenza effettivamente irradiata in condizioni reali.
In figura 2.7 viene mostrata la geometria del modello di sorgente utilizzata per un telefono di ultima generazione.
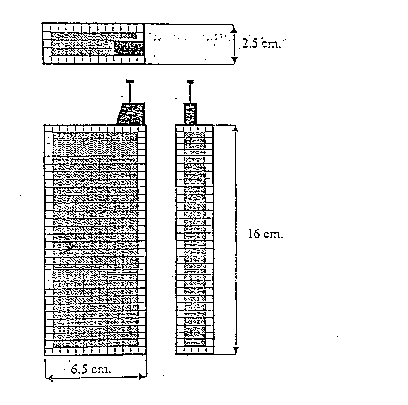
figura 2.7 - modello della sorgente nel caso di telefono di ultima generazione
Essa si riferisce al telefono cellulare MOTOROLA Microtac ™ : le celle scure corrispondono ad un conduttore perfetto e rappresentano la circuiteria elettronica e l'alimentazione, le celle chiare corrispondono all'involucro, simulato con un materiale con caratteristiche elttriche identiche a quelle della gomma. In questo tipo di telefono l'antenna, detta anche whip antenna, è costituita da un monopolo alimentato alla base da una piccola induttanza e da un cappello capacitivo, usato per ridurre le dimensioni fisiche dell'elica. Nella figura 2.8 è riportato l'andamento del modulo del campo magnetico irradiato dal telefono: possiamo notare un picco, in corrispondenza dell'induttanza, ed un non trascurabile contributo radiativo del case, sia nei risultati sperimentali che nella simulazione numerica.
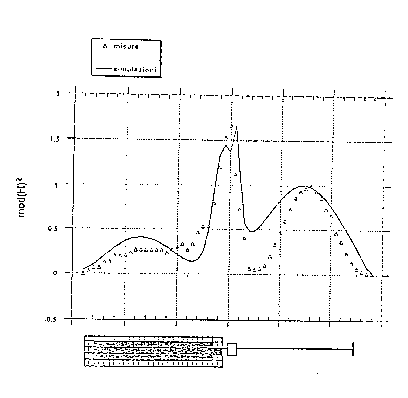
figura 2.8 - andamento del campo magnetico lungo il telefono con whip antenna
Questo dispositivo è in grado di operare anche con l'antenna collassata, in quanto, così, il sistema radiante è costituito dall'induttanza e dal metallo del case. La figura 2.9 evidenzia la maggiore influenza del case nel diagramma radiativo; questo comporta, come detto, che nelle due modalità di uso (antenna aperta o meno) una diversa localizzazione dei valori massimi di SAR nella testa dell'utilizzatore.
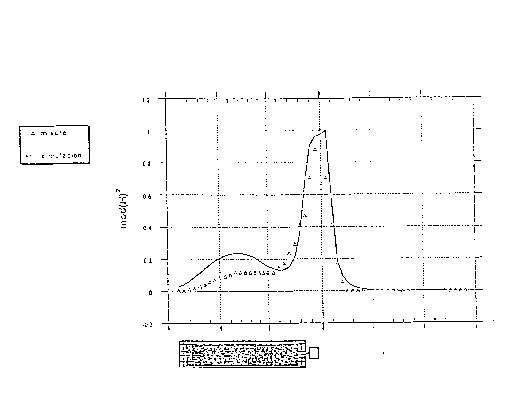
figura 2.9 - campo magnetico lungo il telefono con antenna collassata
La presenza di un essere umano dal punto di vista dell'influenza sulle caratteristiche dell'energia elettromagnetica irradiata dai telefoni portatili e, dunque, del conseguente assorbimento, è stata simulata considerando solamente la testa e la mano che sorregge l'apparecchio; questa assunzione è giustificata dal fatto che l'effetto della presenza del resto del corpo sull'assorbimento nella testa è trascurabile ai fini del nostro lavoro, quando la lunghezza d'onda diventa comparabile con le dimensioni della testa. Ad esempio, nel campo di frequenze compreso tra i 600 MHz ed 1 GHz le differenze ottenute con misure su diversi tipi di fantocci (testa+corpo vs. testa+mano) sono dell'1%.
Il modello disomogeneo della testa si ottiene da immagini TAC o MRI, discretizzate, con l'usuale reticolo FDTD, con risoluzione spaziale normalmente pari a 5 mm, come si vede dalle figure 2.10 e 2.11.
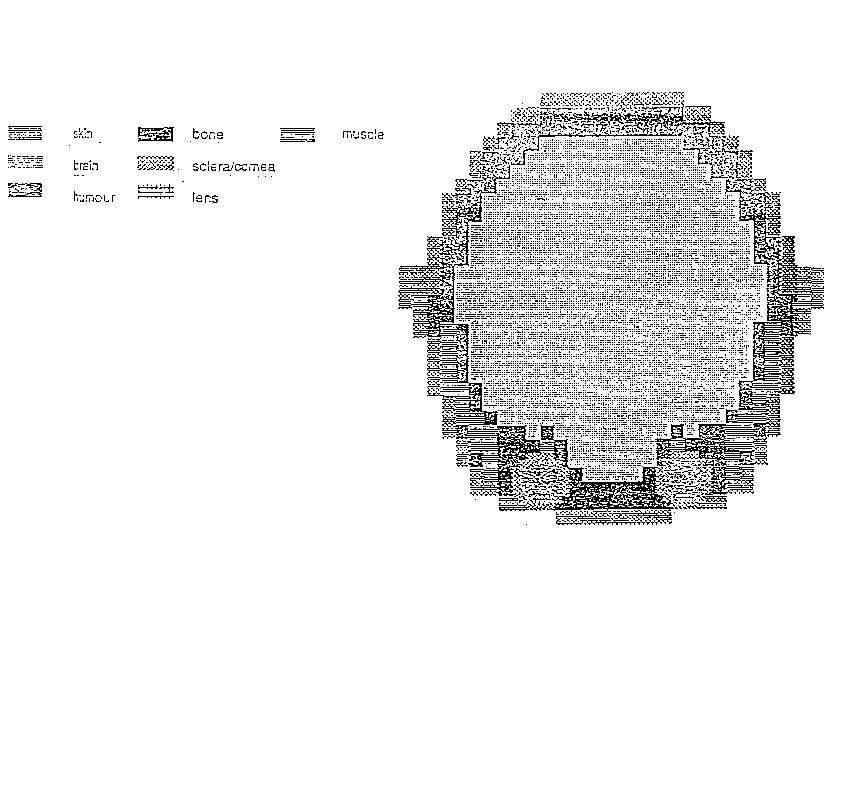
figura 2.10 - sezione trasversale di testa ottenuta da TAC
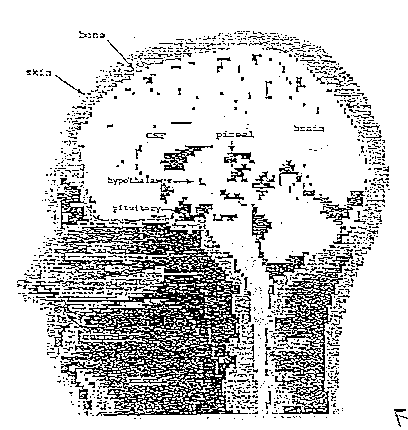
figura 2.11 - sezione verticale di una testa attraverso l'asse sagittale verticale ottenuta da NMR
Nelle prime sperimentazioni che esamineremo il dominio è stato suddiviso in 71x71x81=408321 celle cubiche di 5 mm, alle quali è stato assegnato un preciso valore di conducibilità e costante dielettrica relativo all'aria o al tessuto considerato, alla frequenza operativa di 900 MHz. Le pareti riflettenti sono state simulate imponendo l'annullamento delle componenti tangenziali del campo elettrico sui bordi.
La testa considerata ha le dimensioni di 19.5 cm nelle tre direzioni e, pertanto, risulta contenuta in un dominio cubico formato da 39x39x39 celle di lato 5 mm; sono stati, inoltre, aggiunti tre strati nella direzione z che simulano la parte iniziale del collo, portando il numero delle celle in questa direzione a 42. In totale il numero delle celle che costituiscono il modello della testa è uguale a 26486. Le celle del modello rappresentano alcuni tra i tessuti presenti all'interno della testa: pelle, grasso, muscolo, osso, tendine, cartilagine, materia grigia e bianca, nervi, fluido cerebrospinale, sangue, occhi, come si vede nella figura 2.12.
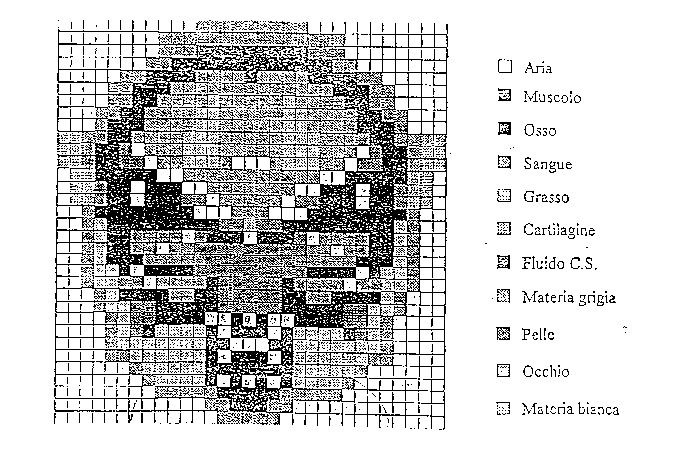
figura 2.12 - sezione della testa nel caso in esame
Nella tabella 2.1 vengono riportati i corrispondenti valori di conducibilità
equivalente e permittività relativa di questi tessuti, alla frequenza
di 900 MHz, insieme ai valori della densità usati per il calcolo
del SAR.
| Tessuto | Conducibilità seq [S/m] | Permettività relativa er | Densità r [g/cm3] |
| Aria | 0.000 | 1.000 | 0.0012 |
| Muscolo | 1.385 | 53.53 | 1.0000 |
| Osso | 0.095 | 7.320 | 1.2000 |
| Sangue | 1.325 | 1.325 | 1.0000 |
| Grasso | 0.110 | 6.200 | 1.0000 |
| Cartilagine | 0.095 | 7.320 | 1.2000 |
| Fluido cerebrospinale | 1.670 | 62.50 | 1.0000 |
| Tendine | 0.095 | 7.320 | 1.0300 |
| Gomma | 0.000 | 2.000 | 1.0000 |
| Materia grigia | 0.670 | 47.40 | 1.0500 |
| Pelle | 0.823 | 43.73 | 1.0000 |
| Occhio | 1.900 | 70.00 | 1.0000 |
| Materia bianca | 0.484 | 39.40 | 1.0000 |
Per il modello della mano si è considerata una geometria schematizzata come in figura 2.13, con le cellette omogenee e con un dielettrico aventi caratteristiche corrispondenti a valori che sono i 2/3 di quelli del tessuto muscolare.
figura 2.13 - modello della mano