In questa sezione si considera il corpo biologico dal punto di vista delle proprietà elettromagnetiche. Poichè non si conoscono tessuti con proprietà magnetiche intrinseche, risulta m=m₀  per ogni  w. La permittività e , invece, nelle frequenze in esame dipende da  w, è cioè del tipo:

e = e (w) = e' (w) - je" (w)              con e' ed e" >=0, "w               (1)

rot H  =  J  + jweE  = (s + we")E  +  jwe'E  =  jwe_c E                                 (2)

Indice Capitolo 4

Indice Generale Tesina 6
 

• i transitori termici sono molto lenti rispetto a quelli E.M., e si possono quindi separare i due problemi considerando che, quando inizia il transitorio termico, il problema EM è già andato a regime.
• il campo emesso dall'applicatore è monocromatico, e allora si può ritenere che il campo nel tessuto sia quasi monocromatico, cioè del tipo:
E ( r ,t ) = E ( r )  * e ^jwt  * p(t)                                                            (3)
ove p(t) rappresenta sia la lenta variazione di ampiezza delle sorgenti, sia la variazione di e con la temperatura, sia del transitorio E.M.

E ( r ,t ) = Re [ E ( r )  * e ^jwt ]                                                                       (4)

Q_EM ( r ) = ( s + we ) * 0.5 * E ( r ) E*( r )                                                  (5)

Indice Capitolo 4

Indice Generale Tesina 6

Dato un campo incidente, si vuole calcolare il campo all'interno del tessuto, e quindi la potenza E.M. deposta in esso. Di fondamentale importanza è conoscere la permittività e in ogni punto del tessuto: spesso, però, essa è conosciuta con approssimazione del 10% e ciò crea problemi di precisione.
Il primo di questi metodi è basato sulla condizione molto restrittiva di geometria planare (sorgente lontana), mentre il secondo è applicabile a casi molto più generici.

4.3.1 Metodo delle Linee di Trasmissione

In prima approssimazione si considera il campo incidente piano ed il corpo del paziente a strati planari: tutto ciò è abbastanza vero se la sorgente è lontana,cioè se la distanza tra di essa ed il corpo è maggiore delle dimensioni caratteristiche del corpo stesso.
Con tali ipotesi ci si trova in una geometria planare e si applica il metodo delle linee di trasmissione:

• onda piana polarizzata linearmente che si propaga lungo asse x con campo elettrico parallelo a y e magnetico parallelo a z .
• per x <x₀  è presente aria, per x₀<x <x₁ pelle (h=h₁), per x₁<x <x₂ grasso (h=h₂), per  x₂< x  muscolo (h=h₃) ( figura 9 ).

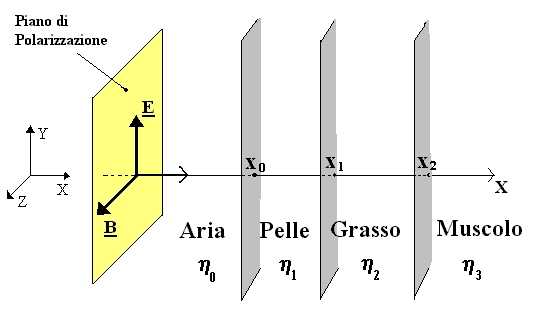Fig.9

E_iy(x) = V_i (x) = V_i⁺* e^-jKx                                                                              (6)
H_iz(x) = I_i (x) = (V_i⁺/h) * e^-jKx                                                                        (7)

V(x) = V⁺ e^-jKx + V^- e ^jKx = V⁺(x) + V^-(x)                                                    (8)
            ( onda diretta + onda riflessa)
I(x) = ( 1/h )( V⁺ e^-jKx - V^-  e ^jKx )                                                                  (9)

Z(x) = V(x)/I(x) = h (1+qv(x)) / (1-qv(x))                                                    (10)

qv(x) = V^-(x)/V⁺(x) = (V^-/V⁺) e ^j2Kx = qv(0) e ^j2Kx                                      (11)

qv(x) = ( Z(x) - h )/( Z(x) + h ) .                                                                   (12)

qv(x₂) = ( h₃ - h₂ )/( h₃ + h₂ )                                                                         (13)

qv(x₁) = qv(x₂) e^-2jK2D2                                                                                   (14)

Z(x₁) = h₂(1 + qv(x₁))/(1 - qv(x₁))                                                                  (15)

Indice Capitolo 4

Indice Generale Tesina 6

4.3.2 Metodo dei Momenti

Si considera una onda incidente generica, proveniente da una sorgente di volume V_S, ed un corpo biologico di volume V e delimitato da una superficie chiusa S ( figura 10 ).
                                                 .

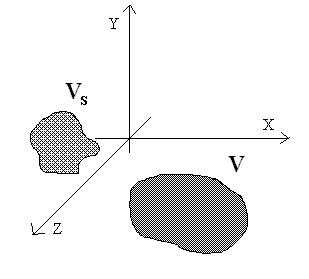Fig. 10

Ñ´E = -jwm₀H                                                                                             (16)
Ñ´H = jwe_cE + J _i                                                                                                             (17)

Ñ´E_i = -jwm₀H _i                                                                                                                           (18)
Ñ´H _i = jwe₀E _i+J _i                                                                                                                     (19)

Ñ´E _s = -jwm₀H _s                                                                                         (20)
Ñ´H _s = J _eq+ jwe₀E _s                                                                                   (21)

E ( r ) - E _i( r ) = -jwm₀[ 1+ ( 1/K₀²)ÑÑ×]  ò_V jw(e_c-e₀) E( r ₁) G( r,r ₁) dV  (22)
E _i( r ) = -jwm₀[ 1+ ( 1/K₀²)ÑÑ×]  ò_Vs J _i( r ₁) G( r,r ₁) dV                           (23)

G = [ e ^{-j K0 | r-r 1|} ]/ 4p| r-r ₁|                                                                      (24)

é Gxx     Gxy     Gxz     ù     é Ex     ù          é   Eix    ù 
ê Gyx     Gyy     Gyz     ú   *   ê Ey     ú  =      ê   Eiy    ú      cioè:  G * E = Ei
ë Gzx     Gzy     Gzz     û     ë Ez     û          ë   Eiz    û

ove E ed E _i sono vettori di 3N elementi. Risolvendo:   E = G^-1 * E _i
L'unica ipotesi fatta è che il corpo sia suddivisibile in volumetti omogenei. Affinchè sia possibile considerare E ed E _i costanti nel volumetto, esso deve avere dimensioni D<<l, ove l è la lunghezza d'onda della radiazione E.M. nel materiale biologico. Questo metodo, però, richiede di immagazzinare nella memoria del computer una matrice G le cui dimensioni (3N*3N) diventano presto proibitive al crescere del numero dei volumetti. Si sono allora messe a punto altre tecniche numeriche basate sull'algoritmo FFT che sfruttano la natura convolutoria dell'integrale di Green.

Avanti nel Capitolo 4

Home Page Tesina 6

Indice Capitolo 4

Indice Generale Tesina 6