Indietro nel Capitolo5

Materiale biologico omogeneo posto all'interno di un condensatore.
 
Polarizzazione tramite spostamento di cariche
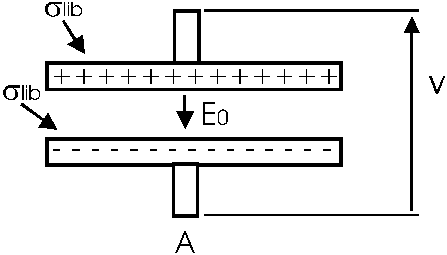
Si può, quindi, considerare un materiale biologico all’interno di un condensatore ( figura 2 ). Inizialmente si applica una differenza di potenziale ad un condensatore; si avrà un rapido transitorio, esaurito il quale ci saranno delle cariche affacciate sulle armature. Si è così ottenuto un campo elettrico statico uniforme e, se si suppone che non vi siano perdite nel vuoto, il condensatore rimane carico. Se si ripete la stessa procedura con un materiale biologico tra le armature (figura 2B), si crea sulla superficie di esso una distribuzione di carica; questa distribuzione dà origine, a sua volta, ad un campo elettrico che si oppone a quello interno al condensatore, con conseguente diminuzione del campo totale. Nei tessuti biologici vi possono essere elevati spostamenti di cariche e quindi forti polarizzazioni e, di conseguenza, valori di e più elevati rispetto agli  altri materiali. All’interno del materiale biologico inserito nel condensatore si avranno due campi vettoriali: il vettore induzione elettrica e0E(t) (che si avrebbe in assenza della polarizzazione del materiale) ed il vettore polarizzazione P(t) che è una misura delle caratteristiche dielettriche del materiale.
 

                        Figura 2

 
 
 
 
 

Con riferimento alle equazioni di Maxwell viste in precedenza si ha:

da cui: dove c è la suscettività elettrica ed indica quanto il materiale reagisce alla presenza del campo (frazione del campo E che viene percepita dal materiale per creare il vettore di polarizzazione P; c assume valori reali e positivi).
Dalla 2) si nota che se er =1  Þ P(t) = 0 e il mezzo si comporta come il vuoto (per esempio Teflon o polistirolo espanso).
Se la risposta del mezzo alle variazioni del campo esterno è istantanea si ha: In realtà, se si fa variare molto velocemente la differenza di potenziale ai capi del condensatore le cariche impiegheranno un certo tempo per spostarsi e raggiungere l’interfaccia del mezzo. Si può fare l’ipotesi semplificativa che la variazione di polarizzazione sia proporzionale, tramite una costante 1/t, alla differenza tra il valore finale ed il valore istantaneo del fenomeno che si sta osservando: questa non è una legge generale perché l’ipotesi  fatta  fissa una ben determinata forma della curva di dispersione ; nel dominio di Laplace la 3) diventa: Supponendo il materiale non polarizzato all’istante iniziale (t=0) allora P(0)=0 e la 4) diventa quindi: da questa si ricava la P(s): nel dominio della frequenza si ha P(jw) = e0cE(jw) / (jwt + 1) .
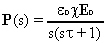
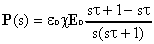
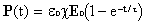
Considerando, adesso, una eccitazione a gradino di ampiezza E0 a t = 0 il vettore P sarà dato dalla: Sommando e sottraendo st nella 5) si ottiene: la 6) può essere riscritta nella forma: Antitrasformando si ottiene: La 8) può essere rappresentata graficamente al variare di t:  

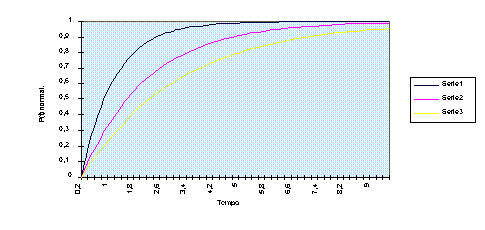
-P(t) normalizzato = P(t)/e0cE0
A commento del grafico è possibile notare innanzitutto che t entra come parametro nella funzione di trasferimento del sistema, tutto ciò conferma che l’ipotesi fatta in precedenza fissa una ben determinata forma della curva di dispersione. Questa costante di tempo dipende dal materiale e dipende dalla  velocità con cui le cariche si spostano nel dielettrico (ad esempio è  possibile pensare agli ioni Na+ che si spostano nella soluzione acquosa). Al variare di t la risposta del sistema sarà più o meno veloce; ad esempio, all’aumentare di t la risposta sarà sempre più lenta.  Considerando i due casi estremi:

Le equazioni 5)- 8) approssimano, quindi, l’andamento di un filtro passabasso.
Si può notare, inoltre, come la 8) sia costituita da due termini: il primo indica quanto il materiale risponde, in termini di intensità, all’eccitazione esterna; il secondo indica ,tramite t con che velocità avviene la risposta.Ovviamente materiali diversi avranno diverse costanti di tempo (per esempio ioni e molecole d'acqua hanno t diverse).
Sempre dalla 8) (relazione che lega P ed E) si nota che, per caratterizzare completamente il materiale è necessario conoscere la  er.
Si può, in generale, supporre l’esistenza di diversi processi di questo tipo, ognuno indipendente dall’altro, per cui si otterrà una sommatoria più un termine  e0E(jw) che si avrebbe se si fosse in presenza solo del vuoto.

Indice del Capitolo 5


Polarizzazione per orientamento e rilassamento dielettrico
Si è, finora, considerata la polarizzazione tramite spostamento di cariche; in realtà, per un generico dielettrico, si può supporre l’esistenza di numerosi processi di polarizzazione di cariche, si avrà, quindi, anche una polarizzazione per orientamento ( fenomeno per il quale i dipoli tendono ad orientarsi secondo la direzione del campo esterno).
Da tutte queste considerazioni è possibile generalizzare la 1):
 
9) 

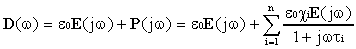
Nella sommatoria n rappresenta il numero di specie chimiche che si trovano all’interno del sistema; c indica quanto è sensibile la singola specie chimica all’azione del campo.
Quando il segnale è a bassa frequenza, la risposta del mezzo é istantanea (nella 8 il termine esponenziale diviene trascurabile); aumentando la frequenza, invece,  P diminuisce (entra in gioco il termine esponenziale e la risposta non è più istantanea). Questo avviene perché i dipoli non riescono più ad orientarsi ( a seguire il campo) e le cariche libere non riescono a spostarsi in modo sufficientemente veloce. Alla frequenza per la quale wt=1 (frequenza di rilassamento) il valore del vettore di polarizzazione P si è dimezzato: metà delle molecole seguono il campo e metà no. Aumentando ancora di più la frequenza, nessuna molecola segue il campo, non si ha polarizzazione e, quindi, er  tende a 1 (Eq. 2). Questo  fenomeno è detto rilassamento dielettrico.
In termini energetici è possibile osservare che in bassa frequenza non si hanno dissipazioni, perché tutte le molecole si muovono insieme; lo stesso discorso vale per le alte frequenze, dato che le molecole non si muovono.
A frequenze dell’ordine di quella di rilassamento sono presenti invece fenomeni dissipativi, questo avviene perché ci sarà attrito tra molecole che seguono il campo e quelle che non lo seguono.
In un tessuto biologico si hanno diverse costanti di tempo, associate a varie specie chimiche (molecole d’acqua, ioni, proteine, etc.). La specie chimica che risponde prima, nel tempo, è l’acqua, la quale funziona a frequenza maggiore rispetto agli altri componenti che tendono a muoversi più lentamente.
Nella 9)  si possono separare parte reale e parte immaginaria:

dove in er¢ e in er² sono contenute le informazioni relative a ti  e ci.

Indice del Capitolo 5


Costante dielettrica relativa complessa
Si può definire una costante dielettrica relativa complessa er* (w) = er¢(w) - jer²(w) e quindi :
                               D(w) = e0 er* (w)E(w)

Sostituendo  er* (w)  nelle equazioni di Maxwell si ottiene:
 

Nella terza equazione è possibile introdurre una conducibilità equivalente: e si ottiene: Il termine aggiuntivo nella geq tiene conto dell’esistenza di conduzione per corrente di spostamento.

Indice del Capitolo 5


Costante dielettrica complessa
Si può definire, in modo equivalente, anche una costante dielettrica complessa che tenga conto dell’esistenza di fenomeni di conduzione a frequenza nulla all’interno del materiale:
  Dalle equazioni viste in precedenza  si ottiene: con  e¢ = er¢  e  e² = er²  +gS/we0 (er² = perdite dovute all’orientazione dei dipoli; gS/we0 = termine legato alla conducibilità, esso diminuisce al crescere della frequenza, infatti agisce solo se la frequenza è minore di alcune decine di MHz ; da notare inoltre che la differenza tra er* e ec è che quest'ultima tiene conto delle cariche libere alla conducibilità : alle alte frequenze esse coincidono).
E’ interessante avere informazioni supplementari su ec dato che è proprio quest’ultima a caratterizzare il materiale; è possibile studiare l’andamento temporale della costante dielettrica. Nel caso più semplice la polarizzazione di un materiale "rilasserà" verso lo stato stabile come un processo del primo ordine caratterizzato da un tempo di rilassamento t; questa costante tempo varia dai picosecondi ai microsecondi per l’orientazione parziale di molecole dipolari per arrivare ai secondi per altri processi di rilassamento. 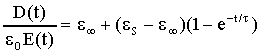La risposta dielettrica di un sistema del primo ordine a una eccitazione a gradino di ampiezza E può essere scritta  nella forma: In essa e¥ deriva dalla polarizzabilità elettronica misurata a frequenza infinita.

Indice del Capitolo 5

  Avanti nel Capitolo 5
 
Homepage tesina 1

  Indice generale tesina 1