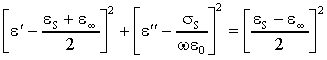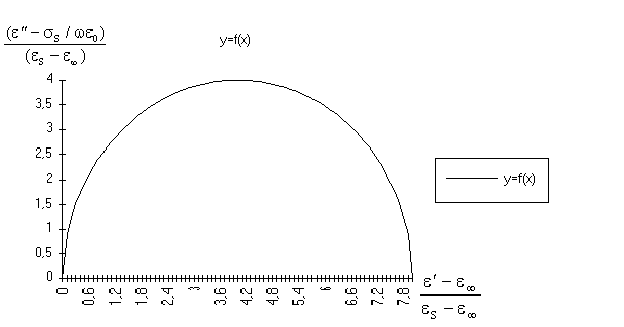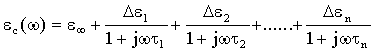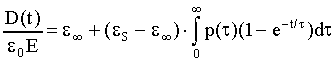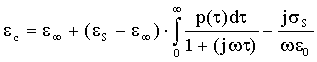Indietro nel Capitolo 5
Indietro nel Capitolo 5
Equazione di Debye
La risposta dielettrica ad un campo sinusoidale E, nel dominio della
frequenza, fu studiata da Debye ed essa si ottiene trasformando l’equazione
14) nel dominio di Fourier:
15) 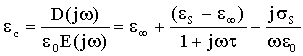
Questa é l’equazione di Debye, che ora è possibile
separare in parte reale e parte immaginaria:
I valori e¥,es,s¥,ss
sono legati dalla relazione:
Se si studia l’andamento di e¢ :
per w ® ¥ si ottiene
e¥ ; per w ®
0 si ha eS.
Questo comportamento tiene conto del fatto che i dipoli si orientano,
in direzione del campo esterno applicato, in bassa frequenza e smettono
di farlo in alta frequenza (rilassamento); questo implica, quindi, che
e¥ < eS
. Inoltre e² è tale che, se si trascura
il termine dovuto alle cariche libere (sS/we0)
, tende a zero sia per w ® ¥
sia per w ® 0. Quindi, questo termine,
che tiene conto delle perdite per orientazione, ha un andamento a "campana"
con il massimo alla frequenza di rilassamento (wt=1).
E’ possibile scrivere, adesso, una relazione di dipendenza dal tempo
per la densità di corrente J analoga a quella vista in precedenza
(Eq. 14) :
16) 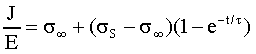
Nel dominio della frequenza questa equazione diventa:
17) 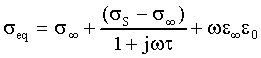
La frequenza di rilassamento fc = 1/2pt
è la frequenza alla quale la permittività è
a metà strada tra i valori di alta e bassa frequenza.
 Indice del Capitolo 5
Indice del Capitolo 5
Andamenti in frequenza di e¢,e²
e seq
Si possono vedere graficamente le considerazioni fatte in precedenza
sull’andamento in frequenza per e¢,
e² e seq.
I grafici seguenti sono normalizzati sia per le ascisse (frequenza)
sia per le ordinate (e¢, e²
e seq) :
FIGURA 4 -Rilassamento a singola costante
tempo.
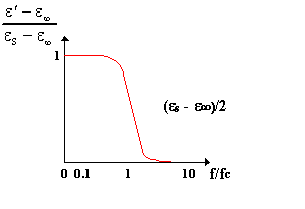 (A)
Permittività relativa in frequenza
(A)
Permittività relativa in frequenza
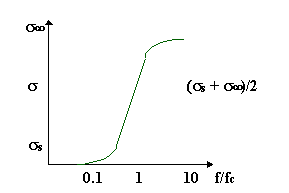 (B)
Conduttività in frequenza
(B)
Conduttività in frequenza
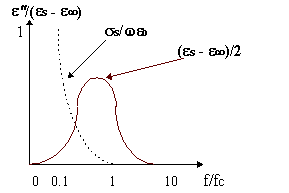 (C)
Perdite in frequenza, è mostrato anche (curva tratteggiata) il contributo
della conduttività in continua (spostamento di ioni)
(C)
Perdite in frequenza, è mostrato anche (curva tratteggiata) il contributo
della conduttività in continua (spostamento di ioni)
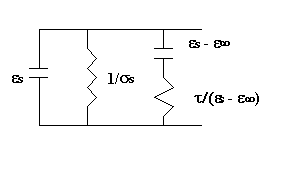 (D)
Circuito equivalente che esprime l’equazione di Debye
(D)
Circuito equivalente che esprime l’equazione di Debye
Nella situazione di singola costante tempo la frequenza
di rilassamento che si osserva in (A) e in (B) è identica; invece,
in presenza di più costanti tempo distribuite la frequenza di rilassamento
mostrata nel grafico (B) sarà, in generale, maggiore di quella
mostrata in (A).
A commento della Figura 4 si osserva che: e²
è costituita da due termini, quello di conducibilità che
decresce all’aumentare della frequenza ed un termine con comportamento
risonante a larga banda (due decadi). Come si è visto
e² è un termine che misura le perdite da riscaldamento
dovute alle oscillazioni dei dipoli; il suo massimo è a f = fc,
frequenza in corrispondenza della quale si ha il massimo attrito (metà
delle molecole seguono il campo e metà no) e cioè il massimo
assorbimento di energia.
 Indice del Capitolo 5
Indice del Capitolo 5
Interpretazione circuitale dell'equazione
di Debye
E’ possibile dare anche una interpretazione circuitale dell’equazione
di Debye ( Fig. 4 D):
1) effetto capacitivo dato dalla e¥
(tiene conto dei fenomeni di orientamento più veloci);
2) effetto resistivo dato dalla 1/sS
(perdite dovute alla conducibilità del materiale);
3) comportamento risonante a fc = 1/t schematizzato
da un circuito RC (la resistenza t/(eS-e¥)
rappresenta le perdite per attrito dovute alla rotazione dei dipoli elementari).
 Indice del Capitolo 5
Indice del Capitolo 5
Rappresentazione nel piano complesso
di ec
Nei grafici precedenti si è visto l’andamento in frequenza di
e¢ ed e²;
è possibile ora rappresentarli con un unico grafico nel piano complesso,
dato che ec = e¢
-je². Se si elimina wt
nelle equazioni di e¢ ed e²
si ottiene la seguente equazione, rappresentabile nel piano complesso:
Da questa equazione si nota che, nel piano complesso, la rappresentazione
della ec, per un fenomeno di
rilassamento a singola costante di tempo, è una semicirconferenza
il cui centro si trova sull’asse reale nel punto e¥
+ (eS - e¥)/2
e il cui massimo si ha per f = fc .
FIGURA 5
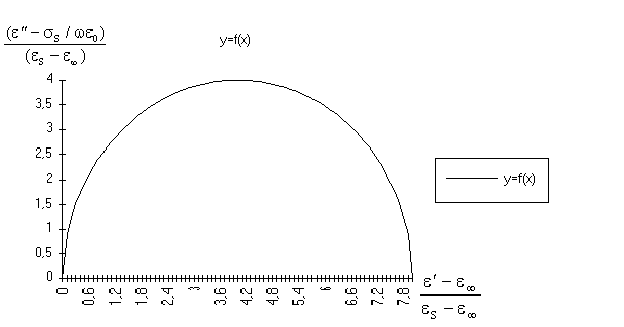
 Indice del Capitolo 5
Indice del Capitolo 5
Rappresentazione in funzione
della frequenza di e¢ e e²
nel caso di più fenomeni di rilassamento
Si è visto finora il caso semplice di singola costante tempo
(in pratica di dielettrico composto da molecole di uguale natura e dimensione);
nel caso reale di interesse, cioè nel quale il dielettrico è
costituito da tessuto biologico, si avranno più fenomeni di rilassamento,
ciascuno con la propria costante di tempo. In prima approssimazione è
possibile considerare il caso in cui le costanti di tempo siano notevolmente
diverse tra loro (t1 <<
t2 << t3
....<<tn ), sotto questa ipotesi
la risposta del dielettrico ad una eccitazione a gradino di ampiezza E
può essere rappresentata come una sovrapposizione di processi del
primo ordine, da cui si ottiene perciò la seguente equazione:
o, nel dominio della frequenza:
18) 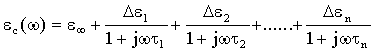
Se è verificata l’ipotesi t1
<< t2 << t3
....<<tn si ottiene, nel piano
complesso, una serie di circonferenze distinte che hanno il centro
sull’asse reale e lo intersecano nei punti:
e¥ ,
e¥ +De1 ,
e¥ +De1 + De2
, ....... e¥
+De1 + De2
+ ......+ Den
FIGURA 6
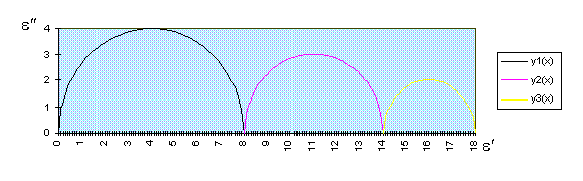
Il massimo per la prima semicirconferenza si ha in corrispondenza di
e¢ = 4, in corrispondenza di tale massimo
si ha la fc dell’ultimo fenomeno di rilassamento; in modo analogo
si hanno gli altri due massimi in e¢
= 11 (fc2) ed in e¢ = 16 (fc3).
Se, invece, si graficano separatamente parte reale e parte immaginaria
della ec si ottengono gli andamenti
riportati in figura per e¢ ed e²:
FIGURA 7
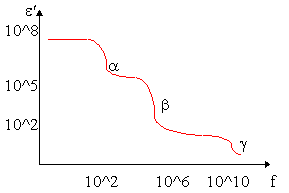
FIGURA 8
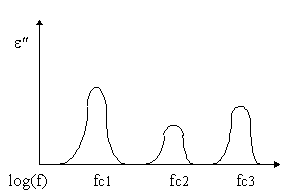
Se non vale l’ipotesi t1 <<
t2 << t3
....<<tn , cioè le varie
costanti di tempo non sono ben separate e se inoltre non si considera vera
l’ipotesi, fatta in precedenza, di variazione di polarizzazione proporzionale
(tramite t) alla differenza tra valore finale
e valore istantaneo di P (dP(t) / dt = 1/t
[e0cE
- P(t)] ), non è più valida l’equazione di Debye.
Si deve, perciò, far ricorso ad una equazione integrale ed introdurre
una p(t) che è una funzione di densità
di probabilità:
19) 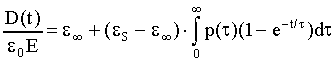
dove, per la p(t) vale la relazione:
p(t) fornisce la percentuale, rispetto
al numero complessivo, delle molecole che hanno una determinata
t.
In questo caso si ha una situazione più complessa, dal punto
di vista del riconoscimento del materiale in esame, perché si devono
specificare dei parametri che permettano di identificare p(t)
e ciò non è semplice visto che i dati sperimentali, sui tessuti
biologici, hanno una certa variabilità.
E’ possibile riscrivere la 19) nel dominio della frequenza e si ottiene
la costante dielettrica complessa:
20) 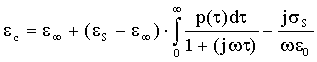
Si è accennato alla difficoltà di determinare con precisione
la p(t) e si deve inoltre sottolineare
che la scomposizione rappresentata nella 19) e nella 20) è solo
un processo formale e il fatto che sia verificata non implica la reale
presenza di fenomeni fisici collegati ad essa.
 Indice del Capitolo 5
Indice del Capitolo 5
 Avanti nel Capitolo 5
Avanti nel Capitolo 5
 Homepage tesina 1
Homepage tesina 1
 Indice generale tesina 1
Indice generale tesina 1
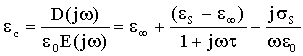
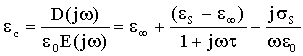
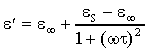
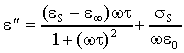
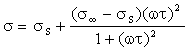
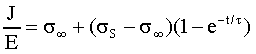
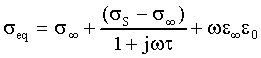
 (A)
Permittività relativa in frequenza
(A)
Permittività relativa in frequenza
 (B)
Conduttività in frequenza
(B)
Conduttività in frequenza
 (C)
Perdite in frequenza, è mostrato anche (curva tratteggiata) il contributo
della conduttività in continua (spostamento di ioni)
(C)
Perdite in frequenza, è mostrato anche (curva tratteggiata) il contributo
della conduttività in continua (spostamento di ioni)
 (D)
Circuito equivalente che esprime l’equazione di Debye
(D)
Circuito equivalente che esprime l’equazione di Debye