 Indietro nel Capitolo 5
Indietro nel Capitolo 5
Funzione di rilassamento di Cole&Cole
Per risolvere il problema di t paragonabili
si sono studiate varie equazioni empiriche che, anche se non conducono
ad una conoscenza approfondita dei meccanismi interni coinvolti, permettono
di parametrizzare i dati sperimentali. Una di queste funzioni di rilassamento
empiriche è quella proposta da Cole & Cole:
Questa equazione può essere separata in parte reale e parte immaginaria:
Al variare della frequenza, l’andamento di e²-sS/we0
in funzione di e¢ è dato,
nel piano complesso, da una circonferenza:
( x - x1 )2 + [ y + ( r - y1 )]2
= r2
dove:
Il massimo della funzione di Cole & Cole si ha per f = fc
dove fc è la frequenza di rilassamento media. Graficamente
si ottengono le figure 9) A e B.
La funzione di distribuzione p(t) che si
dovrebbe inserire nella 19) per ottenere
l’equazione di Cole & Cole è:
dove t0 = (2pfc)-1
è il tempo di rilassamento medio.
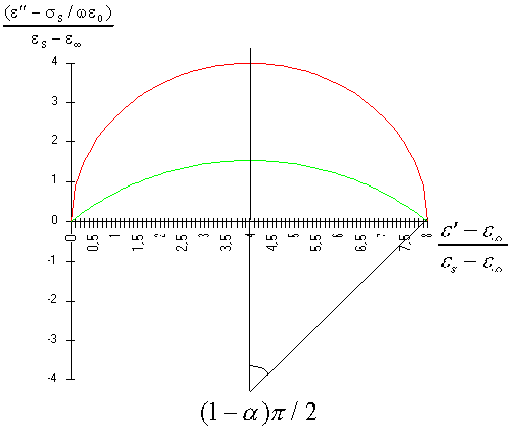
(A) Grafico della permittività complessa
dell’equazione di Cole & Cole (è evidenziato l’andamento semicircolare
schiacciato che è una caratteristica di molti materiali biologici).
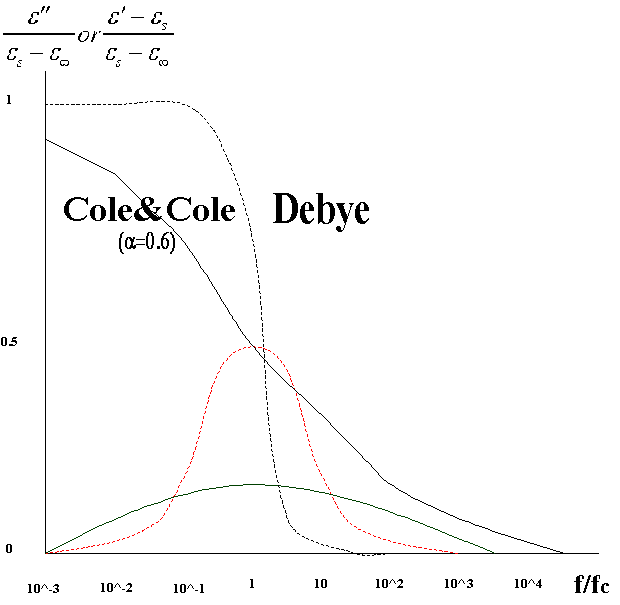 (B) Andamento della permittività e della conduttività
nell’equazione di Cole & Cole; il parametro di distribuzione a
è uguale a 0.6 e ciò equivale a considerare un ampio
intervallo di tempi di rilassamento.
(B) Andamento della permittività e della conduttività
nell’equazione di Cole & Cole; il parametro di distribuzione a
è uguale a 0.6 e ciò equivale a considerare un ampio
intervallo di tempi di rilassamento.
L’equazione di Cole & Cole si riduce a quella di Debye per a
= 0; si osserva dalla figura 9)A che il centro della
circonferenza non si trova sull’asse delle x ma la sua posizione è
funzione di a (parametro di distribuzione).
Il fenomeno descritto da Cole & Cole interessa un campo di frequenze
più ampio perché prende in considerazione dipoli con caratteristiche
diverse che , quindi, rilassano a frequenze diverse, con conseguente allargamento
della banda; perciò, ad ogni frequenza, si hanno più fenomeni
sovrapposti.
 Indice del Capitolo 5
Indice del Capitolo 5
Relazioni di Kramers-Kronig
Siccome la costante dielettrica complessa ec
si riferisce ad un sistema fisicamente realizzabile la sua parte reale
(e¢) e la sua parte immaginaria (e²)
non saranno indipendenti ma dovranno essere consistenti con le relazioni
di Kramers-Kronig:
21) 
22) 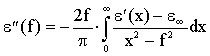
Per valori fissati di eS ed e¥
l’area sotto la curva di perdita, quando la e²
è graficata in funzione del logaritmo di f deve essere indipendente
dalla distribuzione dei tempi di rilassamento; per f ®
0 la 21) diventa:
Le relazioni di Kramers-Kronig derivano da ipotesi molto generali, le principali
sono: la linearità della risposta e la causalità.
Queste relazioni si riferiscono a materiali dielettrici con arbitrarie
distribuzioni di tempi di rilassamento; il limite principale è che
il campo applicato deve essere di intensità tale da permettere una
risposta lineare, si ha cioè una limitazione sul massimo campo applicabile.
Un secondo limite deriva dal fatto che, non sempre, per materiali biologici,
le proprietà del sistema sono invarianti nel tempo, comunque questo
non è un grosso problema dato che una ipotesi del genere rispetta
abbastanza bene la realtà.
 Indice del Capitolo 5
Indice del Capitolo 5
Interazione microscopica
Finora è stato trattato il problema della caratterizzazione
del materiale biologico da un punto di vista macroscopico; si è
cioè studiato il problema del riconoscimento dielettrico (riconoscimento
della composizione di un dielettrico tramite misure esterne).
Lo studio di un materiale può essere affrontato anche sotto
l’aspetto microscopico ed infine si possono trovare delle relazioni che
legano ciò che avviene a livello macroscopico con ciò che
avviene a livello microscopico. Ad esempio, facendo alcune misure dall’esterno
del dielettrico, si trova che la e è
caratterizzata da una certa frequenza di rilassamento; conoscendo poi ciò
che è avvenuto a livello microscopico è possibile dedurre
quali molecole hanno "rilassato" ad una determinata frequenza e quali fenomeni
sono intervenuti a livello atomico e molecolare. In definitiva, quindi,
tratteremo i meccanismi d’ interazione fra c.e.m. e molecole: interazione
microscopica.
 Indice del Capitolo 5
Indice del Capitolo 5
Distinzione tra molecole polari
e non
Le molecole possono essere divise in due classi: polari e non polari.
Le molecole polari hanno, nel loro livello energetico più basso,
un momento di dipolo elettrico m intrinseco
cioè senza applicazione di un campo esterno E; le non polari, in
condizioni di assenza di campo, non hanno momento intrinseco. L’intensità
di un momento di dipolo molecolare è uguale al prodotto tra due
cariche distinte e la loro distanza; come ordine di grandezza è
stata presa la carica dell’elettrone (q = 1,6 ´
10-19 C) moltiplicata per una distanza dell’ordine delle dimensioni
interatomiche (0,25 ´ 10-10
m); storicamente questa grandezza viene misurata in Debye (1 Debye = 3,33
´ 10-30 cm). Lo scopo principale
è di determinare le proprietà delle sostanze dielettriche
contenenti molecole che hanno momento di dipolo intrinseco m,
in assenza di campi o sottoposte a perturbazioni esterne. Si deve osservare
che una molecola libera oltre ad avere il suo moto di traslazione è
dotata anche di moti oscillatori e rotazionali. E’ possibile, comunque,
semplificare la trattazione assumendo che questi ultimi non alterino il
valore medio del momento del dipolo ( 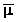 ).
).
 Indice del Capitolo 5
Indice del Capitolo 5
Polarizzazione elettronica, atomica
e dipolare
Quando un campo elettrico E1 viene applicato ad un materiale,
esso influenza le molecole in due modi: in primo luogo perturba la rotazione
libera del dipolo ed in secondo luogo introduce un momento di dipolo aggiuntivo
(aE1). Il momento totale sarà
quindi:
dove a è chiamata polarizzabilità
delle molecole ed è data dalla somma di due termini;
con ae
= polarizzabilità elettronica ed aa
= polarizzabilità atomica.
Nella polarizzabilità elettronica il campo applicato E
causa, in ogni atomo, lo spostamento della nube elettronica rispetto al
nucleo . Nella polarizzabilità atomica il campo E provoca
uno spostamento relativo tra i nuclei di atomi vicini ( Fig. 10)
FIGURA 10
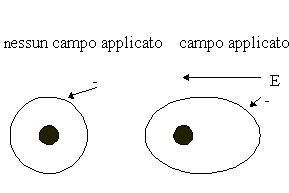
(a) Rappresentazione schematica della polarizzazione elettronica.
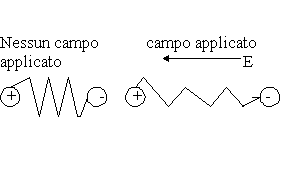
(b) Rappresentazione schematica della polarizzazione atomica.
Si cerca ora un legame tra aspetti macroscopici e microscopici di interazione
esprimendo, perciò, il vettore di polarizzazione P come prodotto
di N (numero di dipoli per unità di volume) ed  (valor medio dei momenti di dipolo sotto l’azione di un campo locale E1):
(valor medio dei momenti di dipolo sotto l’azione di un campo locale E1):
24) P = N =
N(
=
N( 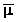 +aE1)
+aE1)
dove 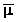 è il valor medio dei momenti di dipolo delle molecole polari. Questa
relazione fornisce l’equivalenza tra il vettore di polarizzazione P e il
momento di dipolo elettrico per unità di volume del materiale; questo
momento è dato, infatti, dall’azione di N momenti di dipolo elementari
cioè appunto N
è il valor medio dei momenti di dipolo delle molecole polari. Questa
relazione fornisce l’equivalenza tra il vettore di polarizzazione P e il
momento di dipolo elettrico per unità di volume del materiale; questo
momento è dato, infatti, dall’azione di N momenti di dipolo elementari
cioè appunto N . La quantità
. La quantità 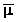 può essere espressa in funzione del campo elettrico esterno applicato;
infatti, sotto l’azione del suddetto campo, i dipoli subiscono l’effetto
di una coppia che tende ad allinearli secondo la direzione del campo. L’agitazione
termica si oppone però a questa tendenza ad orientarsi.
può essere espressa in funzione del campo elettrico esterno applicato;
infatti, sotto l’azione del suddetto campo, i dipoli subiscono l’effetto
di una coppia che tende ad allinearli secondo la direzione del campo. L’agitazione
termica si oppone però a questa tendenza ad orientarsi.
E’ possibile scrivere, dalle osservazioni fatte adesso, la relazione:
25) 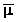 = adE1
= adE1
dove ad è la polarizzabilità
dipolare (orientazione).
FIGURA 11
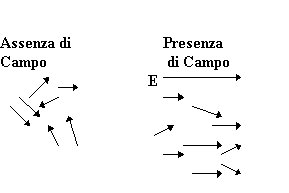
-Rappresentazione schematica della polarizzazione dipolare.
 Indice del Capitolo 5
Indice del Capitolo 5
 Avanti nel Capitolo 5
Avanti nel Capitolo 5
 Homepage tesina 1
Homepage tesina 1
 Indice generale tesina 1
Indice generale tesina 1
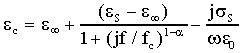
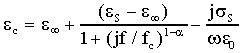
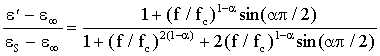
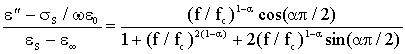
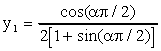
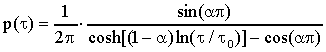

 (B) Andamento della permittività e della conduttività
nell’equazione di Cole & Cole; il parametro di distribuzione a
è uguale a 0.6 e ciò equivale a considerare un ampio
intervallo di tempi di rilassamento.
(B) Andamento della permittività e della conduttività
nell’equazione di Cole & Cole; il parametro di distribuzione a
è uguale a 0.6 e ciò equivale a considerare un ampio
intervallo di tempi di rilassamento.

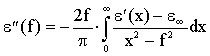
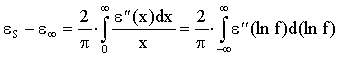


![]() (valor medio dei momenti di dipolo sotto l’azione di un campo locale E1):
(valor medio dei momenti di dipolo sotto l’azione di un campo locale E1):
