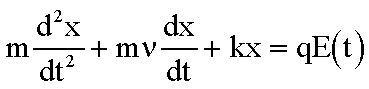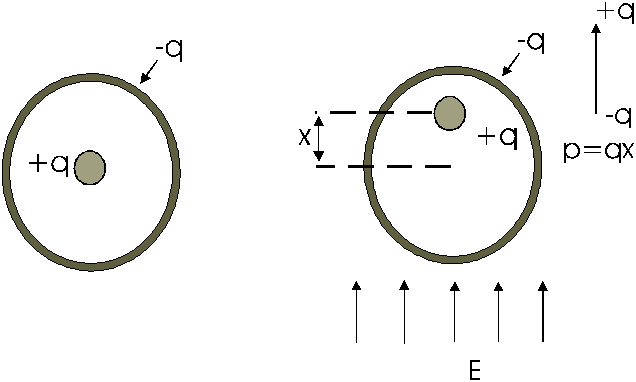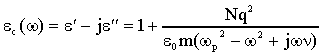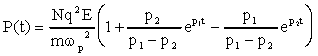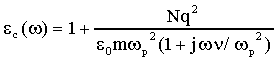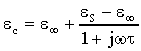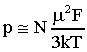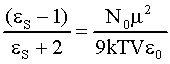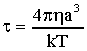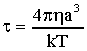Indietro nel Capitolo 5
Indietro nel Capitolo 5
Legame tra approccio macroscopico
e molecolare
Dalle equazioni 23), 24)
e 25) si ottiene:
26) P = N(ad +
ae + aa)E1
e, uguagliando con la P = e0cE
= e0(er-1)E
si ottiene
e0(er-1)E
= N(ad + ae
+ aa)E1 = Nat
E1 Þ
c = (er-1) = NatE1
/ e0E
con at polarizzabilità totale
delle molecole.
Questa relazione è il legame che si cercava fra l’approccio
macroscopico e quello molecolare. Bisogna notare la differenza che c’è
tra il campo locale E1, che agisce a livello molecolare, ed
il campo esterno E applicato al materiale dielettrico. Lo scopo delle teorie
molecolari è quello di valutare e collegare quantitativamente la
permittività er
e la polarizzabilità totale at
per i materiali che di interesse.
 Indice del Capitolo 5
Indice del Capitolo 5
Esempio di un mezzo dielettrico
caratterizzato solo da una polarizzazione elettronica
E’ possibile applicare operativamente questi concetti ad un semplice
esempio nel quale il mezzo dielettrico è caratterizzato solo da
una polarizzazione elettronica (Collin 1966).
Schematizziamo l’atomo con un modello costituito da un nucleo centrale,
carico positivamente (+q), ed una nube elettronica, approssimabile ad una
sfera, con carica totale negativa ( Fig. 12).
L’applicazione di un campo elettrico E sposta la nube elettronica,
rispetto al nucleo, di una quantità x in direzione opposta al campo
applicato; si vengono a creare, perciò, due forze che si oppongono:
una, di richiamo, proporzionale allo spostamento ed una, viscosa, dovuta
ai processi dissipativi, proporzionale alla velocità con la quale
si sposta la nube elettronica.
Si ottiene perciò l’equazione:
27) 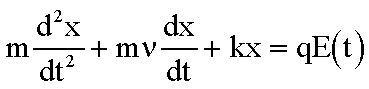
Questa è l’equazione dinamica del moto indotto da un campo elettrico
applicato. In essa m è la massa della nube elettronica; a primo
membro il primo termine rappresenta la forza di inerzia (F = ma), il secondo
la forza viscosa, il terzo la forza elastica di richiamo. A secondo membro
si ha la forza data dal campo elettrico esterno.
FIGURA 12
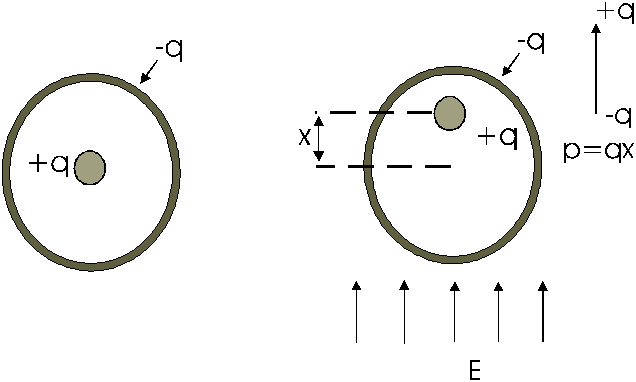
- Modello di un atomo con un nucleo con carica positiva (+q) circondato
da una nube elettronica con carica negativa (-q)
Come conseguenza di questo spostamento di cariche si induce un dipolo
con la stessa direzione del campo applicato: pe =
qx .
Indicando con N il numero di atomi per unità di volume, la polarizzazione
macroscopica del dielettrico è:
Moltiplicando per Nq e dividendo per m, l’equazione 27), nell’ipotesi che
il materiale sia composto da atomi della stessa specie, può essere
scritta , a livello macroscopico, nel modo seguente:
29) 
dove wp2 = k/m.
La soluzione della 29), nel dominio della frequenza e per un campo
esterno sinusoidale, fornisce la seguente espressione per la permittività
complessa:
30) 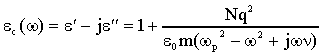
Nel dominio del tempo la risposta ad una eccitazione a gradino applicato
all’istante t = 0 (E(t) = E u-1(t)) è:
31) 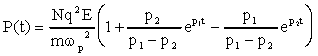
nella quale p1 e p2 sono le radici dell’equazione
caratteristica associata alla 29).
La equazioni appena viste mostrano una risposta dielettrica di un sistema
del secondo ordine sia nel dominio del tempo (31) sia nel dominio della
frequenza (30).
Nei materiali biologici la polarizzazione indotta da un gradino di
campo elettrico rilassa, generalmente, verso lo stato stabile come un processo
del primo ordine caratterizzato da un solo tempo di rilassamento. E’ interessante
notare che, con determinate approssimazioni, risposte del primo ordine
possono essere ottenute anche dalle equazioni 30) e 31).
Se, infatti, wp << n/2
, le due radici p1 e p2 dell’equazione 31) sono entrambe
reali, negative e considerevolmente diverse l’una dall’altra; i tempi di
rilassamento associati alle due radici saranno, perciò, notevolmente
diversi. Se si trascura, quindi, il termine associato alla radice più
alta in valore assoluto, che corrisponde ad una risposta praticamente istantanea,
si ottiene un processo con una sola costante tempo.
Nel dominio della frequenza, se wp
<< n, l’equazione 30) si riduce alla:
32) 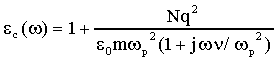
Questa equazione ha la forma di una risposta dielettrica di un processo
del primo ordine e rappresenta l’andamento tipico di materiali con momenti
di dipolo permanenti.
In questo caso la permittività complessa è data da:
33) 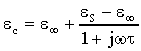
Questa equazione è conosciuta, comunemente, come formula di dispersione
di Debye.
Si può dare adesso una interpretazione fisica del fenomeno,
si nota che le due radici si riferiscono a due meccanismi di polarizzazione
distinti. In particolare, la radice alta corrisponde alla polarizzazione
elettronica che è un fenomeno molto veloce e che quindi si
porta subito a regime. L’altra radice si riferisce, invece, all’orientazione
delle molecole divenute polari per effetto della polarizzazione elettronica
e questo è un fenomeno più lento.
Dalle equazioni 32) e 33) si nota che esiste un legame tra wp
e t, e quindi fra wp
ed fc. Se si ricorda poi che fc dà informazioni
sul materiale a livello macroscopico mentre wp
dà informazioni a livello molecolare (wp
= (k/m)1/2), si ha una relazione tra livello macroscopico e
livello microscopico.
Estendendo le conclusioni dell’esempio appena visto al caso di molecole
complesse (costituite da più atomi) e molecole prive di momento
dipolare proprio, si creano, per effetto del campo esterno, dei momenti
di dipolo molecolari più complicati. Questi dipoli si orienteranno,
quindi, nella direzione del campo, con una costante tempo più lunga.
 Indice del Capitolo 5
Indice del Capitolo 5
Molecole Dipolari
Comportamento dell'acqua
Si può ora considerare il comportamento di molecole dipolari,
come l’acqua : in questo composto l’ossigeno attrae fortemente la nube
elettronica dell’idrogeno e, di conseguenza, si ha la creazione di una
carica positiva dovuta al nucleo di H ed una negativa dovuta allo spostamento
di elettroni verso il nucleo dell’ossigeno.
FIGURA 13
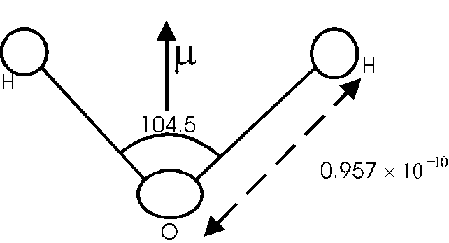
- molecola d’acqua
In presenza di campo elettrico il dipolo sperimenta un momento di torsione.
Se si indica con F l’intensità del campo applicato esternamente
alla molecola e con m il momento di dipolo di
ciascuna molecola, su essa agisce una coppia
mFsinq dove q
è l’angolo tra il campo elettrico ed il momento di dipolo. Tale
coppia tende, quindi, ad orientare il dipolo in direzione del campo, ad
essa si oppone l’agitazione termica che crea un movimento casuale dei dipoli
tendente a spostare le molecole dalla posizione di equilibrio ( moti Browniani).
L’azione opposta di queste due forze crea una situazione nella quale i
dipoli non si orientano tutti nella stessa direzione.
Facendo quindi ricorso alla :
34) < cosq > = coth (mF/kT)
- kT/mF
che mostra un valore medio dell’angolo in funzione di kT; k è la
costante di Boltzmann, kT l’agitazione termica e mF
è la misura di quanto le molecole siano sensibili al campo.
Per campi di intensità moderata, l’energia massima associata
a mF è << dell’energia cinetica
media associata a kT. Dal punto di vista dinamico c’è una diversità
di fondo; infatti, mentre il campo tende ad orientare la molecola sempre
nella stessa direzione, l’energia associata a kT è caotica quindi
prevale l’orientazione costante; con queste ipotesi si ottiene la:
la polarizzazione del materiale è data da:
dove N è il numero di molecole per unità di volume; la 36)
può essere riscritta in maniera approssimata ricorrendo alla 35):
37)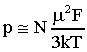
Il campo locale (F) applicato a ciascuna molecola può essere collegato
al campo esterno E mediante l’espressione di Lorentz:
38)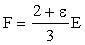
Il modello utilizzato è una sferetta omogenea con permittività
e e con campo applicato E all’interno di uno
spazio sferico circostante. Con questa ipotesi si ottiene, dalla 38), l’espressione
per la permittività relativa statica:
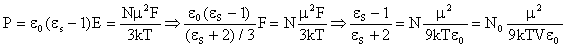
39) 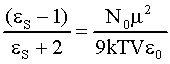
dove N0 è il numero di Avogadro e V è il volume
molare = N0/N; questa equazione lega le caratteristiche interne
del materiale (m) e le caratteristiche macroscopiche
(e).
Dalla 39) si osserva che se m = 0
si ottiene eS = 1; ciò mostra
quanto la presenza della molecola possa influenzare la polarizzazione.
 Indice del Capitolo 5
Indice del Capitolo 5
Legge di Stokes
Si è già visto che le molecole non seguono il campo esterno
istantaneamente ma con un certo ritardo; ci si trova in un fenomeno di
rilassamento (Debye) in cui bisogna identificare con quale t
viene raggiunto l’equilibrio tra il momento dovuto al campo e la viscosità
dovuta all’agitazione termica.
Si utilizza la legge di Stokes:
40) 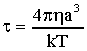
In essa t è la costante di rilassamento
rotazionale, a è
il raggio del dipolo e h è la
viscosità del mezzo. Questa costante tempo varia dai microsecondi,
per grandi proteine globulari, ai picosecondi per molecole polari più
piccole (per esempio acqua); di conseguenza la banda delle frequenze di
rilassamento varia dai MHz ai GHz . Sebbene la teoria di Debye sia interamente
a livello macroscopico si ottengono dei buoni risultati se la si applica
a soluzioni di molecole dissociate e la legge di Stokes è sorprendentemente
buona anche per liquidi fortemente legati, come l’acqua.
L’approssimazione fatta da Debye, per calcolare
t (cioè la legge di Stokes), fu quella di considerare la
molecola sferica in un mezzo viscoso ( in presenza di altre sferette);
le molecole dipolari ruotano sotto l’azione della coppia T del campo applicato
con una velocità angolare proporzionale alla coppia stessa:
41) 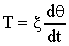
La costante di attrito molecolare x dipende
dalla forma delle molecole e dalle interazioni alle quali sono sottoposte.
La rotazione di queste molecole (approssimate a sfere) è rallentata
dalla viscosità del mezzo esterno; con l’approssimazione di Debye
i calcoli di idrodinamica fatti da Stokes portarono alla :
dove h è la viscosità
macroscopica e a il raggio delle sfere dipolari.
Questa legge dà un legame tra aspetti microscopici
(x) e macroscopici (h);
Debye calcolò, quindi, t in maniera statistica,
rispetto alle grandezze microscopiche; cioè derivò l’orientazione
dei dipoli dalle opposte influenze dei moti Browniani e del campo elettrico
dipendente dal tempo. Ottenne così la:
(costante tempo associata allo spostamento dovuto al campo E ma in presenza
di rallentamento viscoso: tempo medio)
Combinando la 42) e la 43) si ottiene la:
che è proprio la legge di Stokes.
Dalla 40) si nota che, in un mezzo fortemente viscoso (h
grande) t aumenta; se c’è un incremento
dell’agitazione termica (kT) la costante tempo diminuisce perché
aumenta il caos intorno alle particelle ed in un certo senso questo facilita
il loro movimento.
Se si considera, a titolo di esempio, l’acqua, con i seguenti valori:
- a = 2.8´10-10 m
(raggio sferetta) ,
- h = 10-3 Kg/ms (viscosità a 293 K),
dalla 40) si ottiene t = 8.5´10-12
sec. che è un valore in buon accordo con il dato sperimentale (t
= 9.3´10-12 sec.). Il fatto
che il modello delle sfere rotanti dia buoni risultati per il tempo di
rilassamento è piuttosto sorprendente, dal momento che, le molecole
dipolari dell’acqua, a causa del forte legame a idrogeno, hanno una forma
ben lontana da quella sferica in un fluido non polare.
In realtà si è considerato a come la semidistanza
tra due atomi di ossigeno e non come il raggio del dipolo, come si dovrebbe
fare in assenza di interazioni con altre molecole. Infatti, l’acqua , in
presenza di altre molecole tende a risentire della loro presenza, si crea,
cioè, una specie di catena nella quale le molecole sono legate l’una
all’altra. L’acqua esiste in natura in una configurazione a tetraedro,
con l’ossigeno ai vertici, questo è un legame molto forte ed è
dovuto alla mutua generazione di campo elettromagnetico tra le varie molecole.
La configurazione a tetraedro fa sì che, all’esterno di essa
non vi sia sbilanciamento di carica; è , in realtà, tutta
la struttura che si muove sotto l’azione di un campo elettromagnetico esterno.
 Indice del Capitolo 5
Indice del Capitolo 5
Curva di dispersione dell'acqua
pura
In corrispondenza al t ricavato con la 40)
si ottiene una frequenza di rilassamento fc = 18.7 G Hz, si può
quindi rappresentare graficamente la curva di dispersione dell’acqua (cioè
l’andamento di e¢ in funzione della frequenza).
FIGURA 14
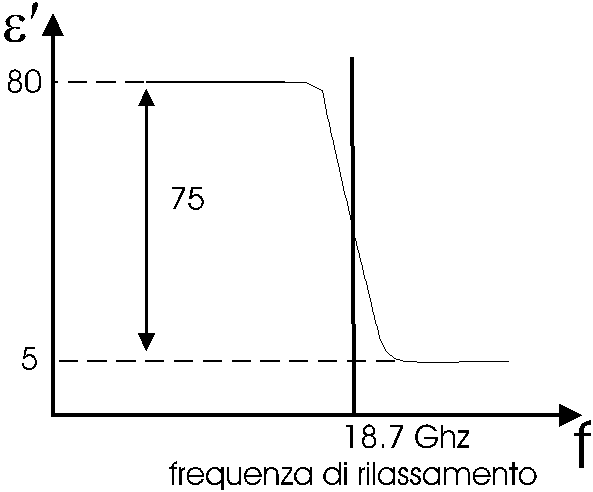 - curva di dispersione dell’acqua pura.
- curva di dispersione dell’acqua pura.
Dal grafico si evince che fino ai 18 G Hz circa le molecole d’acqua
seguono bene il c.e.m. (con e¢ = 80 );
poi alla frequenza di 18.7 G Hz (frequenza di rilassamento) si ha un elevato
salto della costante dielettrica perché metà delle molecole
non riesce più a seguire il campo; infine a frequenze superiori
ai 19 G Hz la e¢ si stabilizza a valori
bassi (5) cioè c’è una piccola parte di molecole che riesce
a seguire il campo. A queste frequenze si ha quindi il fenomeno della polarizzazione
residua dovuta alla sola polarizzazione elettronica. Poiché la polarizzazione
si oppone al campo, una costante dielettrica elevata indica che c’è
poco campo che penetra all’interno; soprattutto in bassa frequenza il campo
vede un dielettrico schermante a causa dell’elevata costante dielettrica.
 Indice del Capitolo 5
Indice del Capitolo 5
Proprietà dielettriche
di alcune proteine
Dato che l’acqua costituisce circa l’80% dei tessuti morbidi, lo studio
della sua permittività dielettrica è molto importante. I
tessuti sono però materiali complicati, cioè composti di
acqua, varie proteine ecc., si ha dunque un andamento leggermente diverso
della dispersione con la frequenza. In particolare, considerando la tabella
4, si nota che la frequenza di rilassamento si abbassa per la presenza
di proteine disciolte in acqua. Dalla prima colonna della tabella si nota
che aumentando il peso molecolare delle proteine presenti in acqua
cresce la costante di rilassamento e, di conseguenza, la fc si sposta in
basso.
TABELLA 4
PROPRIETÀ’ DIELETTRICHE DI ALCUNE
PROTEINE A 250 C
|
Proteine
|
Peso molecolare
(´ 103)
|
De/g/l
|
m( in Debite)
|
t ´ 10-12 (sec.)
|
a/b
|
|
Ovalbumine
|
44
|
0.10
|
250
|
18; 4.7
|
5
|
|
Siero-albumine (cavallo)
|
70
|
0.17
|
380
|
36; 7.5
|
6
|
|
Carbossiemoglobine (cavallo)
|
67
|
0.33
|
480
|
8.4
|
1.6
|
|
Pseudo-globuline di siero (cavallo)
|
142
|
1.08
|
1100
|
250; 28
|
9
|
|
b-lattoglobuline (in 0.25 M glicine)
|
40
|
1.51
|
730
|
15; 5.1
|
4
|
|
Mioglobine
|
17
|
0.15
|
170
|
2.9
|
|
- Peso molecolare in Daltons ; m = momento
dipolare (in Debye); t = tempo di rilassamento
rotazionale; a/b = rapporto assiale; De/g/l
= incremento complessivo della permittività per grammo di proteina
per grammo di soluzione.
Ricapitolando in un materiale biologico esposto ad un campo si manifestano
diversi fenomeni:
-
uno spostamento di ioni che seguono il campo fino a certe frequenze;
-
orientazione delle molecole con rilassamento e risonanza delle perdite
alla Debye;
-
una polarizzazione atomica nella zona dell’infrarosso che manifesta un’interazione
tra gli atomi delle molecole;
-
polarizzazione elettronica.
 Indice del Capitolo 5
Indice del Capitolo 5
 Avanti nel Capitolo 5
Avanti nel Capitolo 5
 Homepage tesina 1
Homepage tesina 1
 Indice generale tesina 1
Indice generale tesina 1