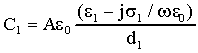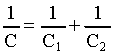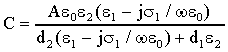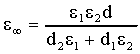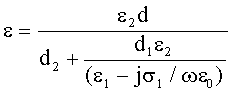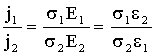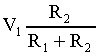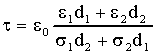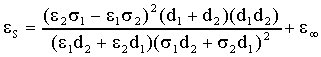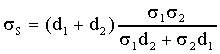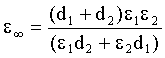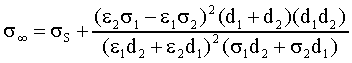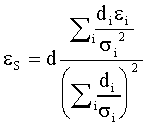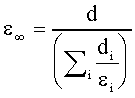Indietro nel Capitolo 5
Indietro nel Capitolo 5
Materale biologico non più
omogeneo posto all'interno di un condensatore
Polarizzazione da interfaccia
Si può considerare adesso un materiale non più omogeneo;
si suppone di avere un mezzo costituito da due parti omogenee e si studia
cosa avviene al livello della giunzione. In natura un esempio di questo
tipo è la cellula che, nella sua schematizzazione più semplice,
è costituita da una prima membrana che racchiude al suo interno
dell’acqua (er =80), isolandola dall’esterno;
internamente è presente anche un’altra membrana che racchiude il
nucleo.
Le membrane cellulari sono composte da un doppio strato fosfolipidico
( i fosfolipidi sono materiali organici che possiedono momento di dipolo
sulla testa) e ciascuno dei componenti è una piccola catena molecolare.
La er della membrana è
pari circa a 2,1.
Nel nucleo c’è il DNA cioè catene molecolari, con
costante dielettrica intermedia tra quella dell’acqua e quella delle membrane.
Tutto ciò dimostra come, già a livello molecolare, vi
siano discontinuità e quindi non si avrà mai una struttura
omogenea come quelle considerate finora. Si è perciò
in presenza di discontinuità tra i mezzi costituenti la cellula.
L’interno e l’esterno del mezzo sono conduttori e se a questo materiale
si applica un campo si ha un meccanismo di polarizzazione da interfaccia
(Maxwell-Wagner).
Per studiare questo meccanismo si considerano due lastre di materiale
omogeneo di spessore d1 e d2, costanti dielettriche
e1 ed e2
e conduttanze s1 e s2
all’interno di un condensatore a facce piane parallele.
FIGURA 15
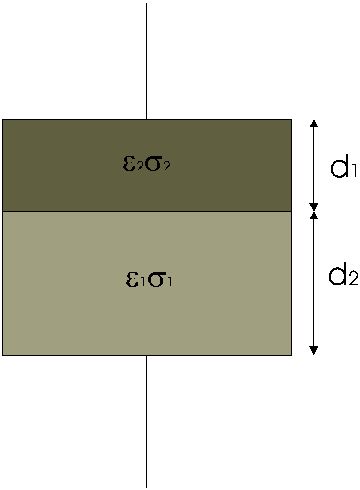 L’interfaccia tra le due lastre è quindi orientata perpendicolarmente
alla direzione del campo esterno. Se all’interfaccia non ci sono cariche
libere, i vettori spostamento sono uguali:
Si suppone, per semplicità, che il secondo materiale sia un dielettrico
perfetto (s2 = 0) e che e1,
e2 e s1
siano indipendenti dalla frequenza. Ciò vuol dire che le costanti
dielettriche e1 ed e2
hanno una parte reale e¢ ¹ 0 mentre
la loro parte immaginaria e² è trascurabile,
pur essendoci fenomeni di perdite per conduzione. La ragione per la quale
e² non viene considerata è che le
bande di frequenza che si considerano sono esterne alla zona di risonanza
delle perdite (siamo cioè lontani dalla fc).
L’interfaccia tra le due lastre è quindi orientata perpendicolarmente
alla direzione del campo esterno. Se all’interfaccia non ci sono cariche
libere, i vettori spostamento sono uguali:
Si suppone, per semplicità, che il secondo materiale sia un dielettrico
perfetto (s2 = 0) e che e1,
e2 e s1
siano indipendenti dalla frequenza. Ciò vuol dire che le costanti
dielettriche e1 ed e2
hanno una parte reale e¢ ¹ 0 mentre
la loro parte immaginaria e² è trascurabile,
pur essendoci fenomeni di perdite per conduzione. La ragione per la quale
e² non viene considerata è che le
bande di frequenza che si considerano sono esterne alla zona di risonanza
delle perdite (siamo cioè lontani dalla fc).
E’ possibile quindi schematizzare il nostro problema tramite la serie
di due condensatori di capacità complesse C1 e C2
:
44) 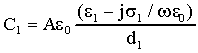
45) C2 = Ae0e2/d2
La capacità complessiva è data quindi dalla serie :
dalle 44) e 45) si ottiene in definitiva :
46) 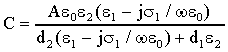
Dalla 46) si vede che C e quindi la permittività totale dipendono
dalla frequenza (comportamento dispersivo).
E’ possibile analizzare l’andamento della costante dielettrica complessiva
al variare della frequenza:
- alle basse frequenze (w ® 0) si
ottiene :
47) eS = e2d/d2
= e2(1+d1/d2)
dove d = d1+d2
- alle alte frequenze (w ® ¥)
si ottiene:
48) 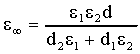
La 48) rappresenta la costante dielettrica di due condensatori in serie.
Alle basse frequenze gli ioni tendono a portarsi all’interfaccia: è
come se si avesse un condensatore con armature più vicine , cioè
a distanza d2 (spessore del secondo materiale).
Dalla 47) si nota che la capacità varia di un fattore d2/d.
Alle alte frequenze gli ioni non riescono più a seguire il campo
e l’unico contributo è quello delle costanti dielettriche, è
come se il condensatore non avesse perdite per conduzione. La e
è caratterizzata da rilassamento con perdite di risonanza, le quali
non sono riconducibili alla s che interviene
in bassa frequenza ma dipendono dal meccanismo di polarizzazione da interfaccia.
La e complessiva in funzione della frequenza
sarà:
49) 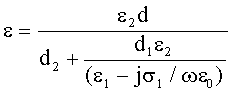
che per w ® 0 e w ®
¥ si riconduce alla 47) e 48) rispettivamente.
Il fenomeno di rilassamento avviene nell’ipotesi che i dipoli del dielettrico
seguano il campo elettromagnetico ed è dovuto, quindi, al meccanismo
di polarizzazione che si crea all’interfaccia. All’interno dei due materiali
non si hanno, invece, fenomeni di rilassamento nell’intervallo di frequenze
considerato (bassa frequenza).
La fc che si ottiene è funzione dello spessore del
materiale, della conducibilità, di e1
ed e2 e dipende da aspetti chimico-fisici.
Dalle 47) e 48) si nota che eS
> e¥; vediamo la spiegazione
fisica di questa disuguaglianza:
nel mezzo 1 si è in presenza di fenomeni conduttivi (cariche
che si muovono lungo lo spessore d1), nell’altro si hanno dei
dipoli; se si applica un campo in bassa frequenza le cariche libere del
mezzo 1 tendono a spostarsi verso il mezzo 2 e si fermano sull’interfaccia
perché quest’ultimo non è conduttore; si ha perciò
una costante dielettrica eS che è
una parte di quella originale. All’aumentare della frequenza il campo cambia
polarità più velocemente e le cariche non riescono a raggiungere
l’interfaccia con conseguente diminuzione della costante dielettrica (e¥)
(serie di due condensatori).
Si può vedere adesso il caso in cui entrambi i mezzi sono conduttori
(s1 e s2
¹ 0); come prima approssimazione si studia il caso statico
(w = 0).
Le conducibilità dei due materiali sono, in generale, diverse;
le densità di corrente all’interfaccia sono legate dalla:
50) 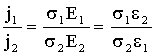
Se le densità di corrente j sono diverse (s1e2
¹ s2e1),
è possibile avere due casi:
-
j1 > j2 : all’interfaccia si accumulano delle
cariche;
-
j2 > j1 : dall’interfaccia vengono portate
via delle cariche.
 Indice del Capitolo 5
Indice del Capitolo 5
Schematizzazione circuitale del
problema: partitore Compensato
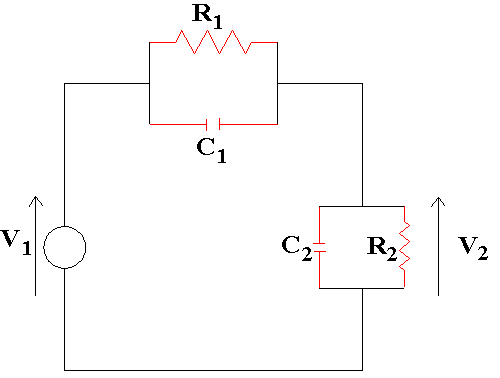
Si può schematizzare tutto ciò con il modello in figura:
FIGURA 16
La figura rappresenta la serie di due paralleli condensatore- resistenza,
le due resistenze tengono conto dei fenomeni di perdita.
Lo schema appena visto rappresenta un partitore compensato.
Si può descrivere brevemente il suo funzionamento: è
possibile fare in modo che i due condensatori si carichino contemporaneamente
(stessa costante di tempo), ciò avviene se vale la :
Con riferimento allo schema e supponendo vera la 51) si ottiene che la
funzione di trasferimento V2/V1 non ha poli; se ,
per esempio, si considera un ingresso a gradino l’uscita sarà ancora
un gradino di ampiezza funzione del rapporto R2/R1.
All’applicazione del gradino si avrà, in corrispondenza del fronte
di salita, una zona a frequenza molto elevata nella quale è possibile
trascurare il contributo di R1 ed R2; si avrà
perciò un partitore capacitivo.
Il segnale in ingresso si ritroverà in uscita modificato di
un fattore C1/(C1+C2); dopo il fronte
ci sarà un segnale di ingresso a frequenza nulla, i due condensatori
tenderanno ad aprirsi ed entreranno in gioco le due resistenze. Si avrà,
quindi, un partitore resistivo che darà una uscita pari a :
Se inoltre vale la 51) si nota che i due fattori C1/(C1+C2)
ed R2/(R1+R2) sono uguali; in uscita si
avrà quindi un gradino del quale è possibile regolare l’ampiezza
modificando i valori delle resistenze e delle capacità. Nei casi
reali la risposta non sarà istantanea ma ci sarà un transitorio
caratterizzato da una costante di tempo t, dopo
il quale l’uscita si riporterà a regime.
Se si applica un gradino , in uscita ci sarà una risposta quasi
immediata; si tratta in pratica di un sistema con una sola costante tempo:
52)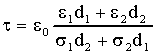
Questo è il tempo di rilassamento per la polarizzazione da interfaccia,
fenomeno studiato da Maxwell-Wagner; si ha poi:
dove 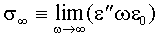
In definitiva, all’interfaccia tra due materiali ci sarà un meccanismo
di dispersione, salvo il caso in cui le due correnti sono uguali (eS
= e¥); se si considera la 53),
questa uguaglianza è verificata quando non si ha salto di impedenza,
cioè scompare il fenomeno di dispersione da interfaccia. Questo
meccanismo è dato dalla variabilità, nel transitorio,
del flusso di corrente che passa da un materiale all’altro; per non avere
dispersione non è perciò sufficiente avere e1
= e2 .Mediante le equazioni 52) e
53) si è in grado di conoscere il salto di costante dielettrica
e la frequenza corrispondente; queste ultime sono le due grandezze sufficienti
a caratterizzare un andamento della costante dielettrica secondo i meccanismi
spiegati da Debye.
La trattazione fatta per due materiali può essere estesa a più
elementi, ottenendo quindi le equazioni:
 Indice del Capitolo 5
Indice del Capitolo 5
Esempi numerici per sistemi a
due strati
Infine nella tabella 5 sono riportati alcuni esempi numerici per sistemi
a due strati, con caratteristiche simili a quelle che possono essere considerate
rilevanti per materiali biologici idratati.
In questa tabella si tiene fissa la dimensione del mezzo 1 (d1
= 1mm) e la sua costante dielettrica (e1
= 2.7) e vengono modificate le caratteristiche del mezzo 2.
Inoltre em²
= (eS -e¥)/2
è il massimo fattore di perdita (cfr. Debye) ed fm =
1/2pt è la frequenza alla quale e²
= em².
La e1
è vicina al valore della e per la membrana
cellulare mentre le varie e2 sono
quelle dell’acqua pura o con proteine disciolte. Si può vedere come
em²
ed fm siano più sensibili alle variazioni della conducibilità
che a quelle di d2 ( spessore).
TABELLA 5
|
d2(mm)
|
e2
|
s2(mho/m)
|
s1 (mho/m)
|
em²
|
fm(Hz)
|
|
10-3
|
80
|
10-4
|
10-10
|
5´10-5
|
6.5´105
|
|
10-1
|
80
|
10-4
|
10-10
|
5´10-3
|
1.7´105
|
|
10-1
|
79
|
1
|
10-10
|
5.1´10-3
|
1.7´109
|
|
10-3
|
95
|
10-9
|
10-10
|
4´10-5
|
6.6
|
|
10-1
|
95
|
10-9
|
10-10
|
2.6´10-2
|
1.5
|
|
10-3
|
95
|
10-12
|
10-10
|
390
|
7.1´10-3
|
 Indice del Capitolo 5
Indice del Capitolo 5
 Homepage tesina 1
Homepage tesina 1
 Indice generale tesina 1
Indice generale tesina 1