(continuo Cap. 2.3)
La tabella 1 mostra invece come si modificano in funzione della potenza, cioè del SAR fornito, i valori di altri due parametri di interesse: la resistenza e il potenziale di membrana. Si osserva, dopo un certo tempo, un aumento della resistenza di membrana pari circa al 7%, e una non significativa variazione del potenziale di membrana, avendo considerato non solo il segnale a 2450 Mhz, ma anche il rumore sovrapposto. I valori ottenuti sono delle medie più o meno un errore standard. I valori fra parentesi indicano il numero degli esperimenti.
Tabella 1
|
Effetti delle microonde di rumore-modulato sulla resistenza d'ingresso e sul potenziale di membrana di neuroni di lumaca |
|||||||||
|
Potenza Assorbita |
Pre-esposizione |
Esposizione |
|||||||
|
30 minuti |
60 minuti |
||||||||
|
P (W/kg) |
R (M W ) |
Vm (mV) |
R (M W ) |
Vm (mV) |
R (M W ) |
D R(M W ) |
D R/r(%) |
Vm (mV) |
D Vm(mV) |
|
14.4 |
16.2 ± 2.3(14) |
51 ± 2(15) |
16.5 ± 2.4(14) |
51 ± 2(15) |
17.3 ± 2.7(14) |
1.1 ± 0.5(14) |
+7 P<.05 |
51 ± 2(15) |
0.3 ± 0.4(15) |
|
6.8 |
13.3 ± 2.3(12) |
51 ± 2(10) |
13.7 ± 2.2(12) |
51 ± 2(10) |
14.2 ± 2.2(12) |
0.9 ± 0.4(12) |
+6.7 P<.05 |
51 ± 2(10) |
0.2 ± 0.9(10) |
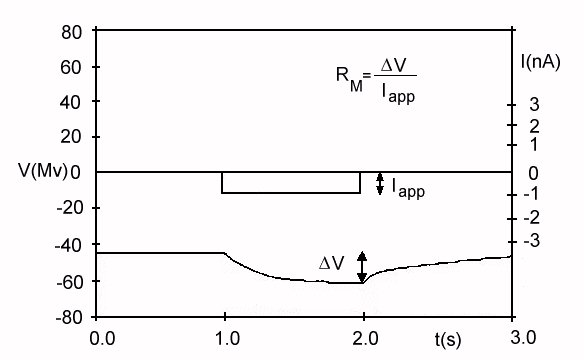
Per ciò che concerne il calcolo della resistenza di membrana, si tratta, come schematizzato in figura 17, di fornire un impulso di corrente e, valutata la variazione del potenziale, di calcolare semplicemente un rapporto. Naturalmente ciò presuppone una linearizzazione del comportamento del neurone.
Avendo fino a questo momento analizzato tutta una serie di esperimenti sul singolo neurone, si ritiene opportuno elaborare un modello che ne schematizzi il funzionamento. Ciò che si può fare è complicare leggermente il modello di Hodgkin e Huxley, come rappresentato in figura 18. Infatti, alla capacità di membrana, al canale sodio, al canale potassio ed alla corrente di perdita, si aggiunge una corrente di calcio, due correnti di potassio, una veloce ed una lenta (al posto di una soltanto), una corrente di potassio controllata dal calcio e, infine, due correnti, di pace-maker e di background, necessarie affinché il modello si accordi nel migliore dei modi con i dati sperimentali.
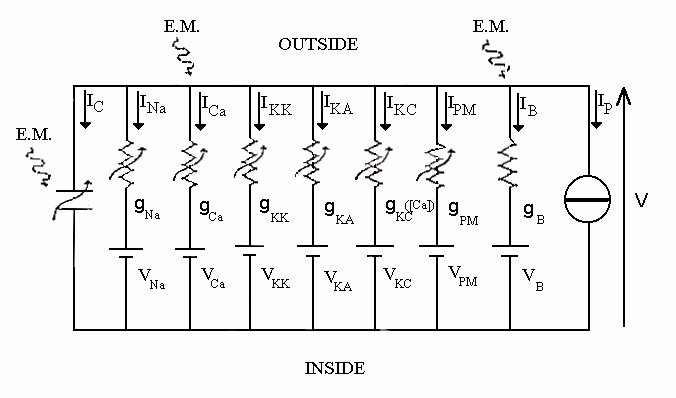
Figura 18
E’ ulteriormente riportata, in figura 19 una parte del modello che rappresenta quanto accade dinamicamente al calcio a livello intracellulare. In essa la produzione di calcio è controllata da Ip (corrente di perdita), IB (corrente di background) e ICa (corrente di calcio). E’ inoltre presente un sistema di regolazione che ci consente di confrontare il valore finale di calcio, col valore in condizioni normali [Ca]0 e, pertanto, di valutare in che misura il campo elettromagnetico ne influenzi il flusso.
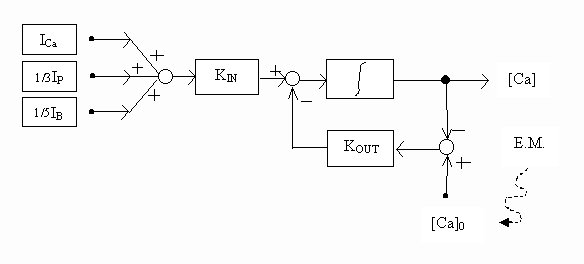
Figura 19
La tabella 2 fornisce i valori dei parametri associati a ciascun canale. Viene fornita una conduttanza statica, ossia per tensioni pari a zero, il potenziale di ciascun canale, in sostanza il generatore associato nel modello, i termini di attivazione e disattivazione, e i rispettivi tempi.
Tabella 2
|
|
gSO (mV) |
VSO (mV) |
AS(V, ¥ ) |
BS(V, ¥ ) |
t AS(V) |
t BS(V) |
||||||
|
VC (mV) |
VP (mV) |
VC (mV) |
VP (mV) |
F (ms) |
VC (mV) |
VP (mV) |
F (ms) |
VC (mV) |
VP (mV) |
|||
|
SODIUM |
30.0 |
44.2 |
-21 |
-6 |
-30 |
3 |
34..5 |
-28 |
12 |
460 |
-30 |
0 |
|
CALCIUM |
8.0 |
61.1 |
8 |
-4.5 |
-20 |
4 |
100 |
27 |
30 |
1760 |
14 |
12 |
|
TRANSIENT POTASSIUM |
10.6 |
-62.0 |
-58 |
-10 |
-75 |
6 |
20.8 |
¥ |
0 |
460.5 |
¥ |
9 |
|
DELAYED POTASSIUM |
8.7 |
-57.9 |
-7 |
-10 |
|
|
135 |
9 |
11 |
|
|
|
|
CA-ACTIVATED POTASSIUM |
9.0 |
-57.1 |
VHI |
-8 |
|
|
1000 |
12 |
15 |
|
|
|
|
PACEMAKER |
.005 |
44.2 |
-35 |
-10 |
|
|
10000 |
-100 |
29 |
|
|
|
|
BACKGROUND |
.0085 |
44.2 |
|
|
|
|
|
|
|
|
|
|
A partire dunque dai dati a disposizione è possibile ottenere una simulazione completa del comportamento elettrico del neurone.